螺旋功率谱检测OAM模式值--MATLAB仿真

1.螺旋谱理论

2005年，Torner L等人发现任何OAM光束\(u(r,\theta ,z)\)能够分解为一系列螺旋谐波函数\(exp(il\theta)\)的线性叠加，即螺旋谱：

\[u(r,\theta ,z)=\frac{1}{\sqrt{2\pi}}\sum_{l=-\infty}^{\infty}a_l(r,z)exp(il\theta) \]

其中，\(a_l(r,z)=\frac{1}{\sqrt{2\pi}}\int_{0}^{2\pi}u(r,\theta ,z)\cdot exp(-il\theta) d\theta\)
若对\(a_l(r,z)\)径向积分则得到\(P_l\)代表了经分解后，不同模态分量上OAM光束的相对功率值：

\[P_l=\int_{0}^{\infty}|a_l(r,z)|^2rdr \]

则光束的总功率表示为：

\[P=\int_{0}^{2\pi}\int_{0}^{\infty}|u(r,\theta ,z)|rdrd\theta =\sum_{l}P_l \]

由\(P_l\)和\(P\)可得到任何OAM光束的螺旋谱：

\[R_l=\frac{P_l}{P} \]

在OAM通信系统中, 信息是通过不同的OAM模式传输的. 接收端需要准确识别出这些模式以正确解调接收到的信号. 螺旋谱提供了一种量化各个模式的相对功率的方法, 有助于解调过程中正确识别和重建信号.

2.代码

2.1 生成OAM涡旋光束(拉盖尔-高斯光束)

2.1.1 文件"lg_oam.m"

function [LG_OAM]=lg_oam(L,w0,P,lambda,x,y)
    % x=linspace(-T*w0,T*w0,N);
    % y=linspace(-T*w0,T*w0,N);
    [px,py]=meshgrid(x,y);
    r=sqrt(px.^2+py.^2);
    phai=atan2(py,px);
    z=0;
    k0=2*pi./lambda;
    zR=pi*w0^2/lambda;
    wz=w0.*sqrt((z.^2+zR.^2)./zR.^2);
    Clp=sqrt(2.*factorial(P)./(pi.*factorial(P+abs(L))));
    X=2*(r.^2)./wz^2;
    LG_poly=0;
    for n=1:P+1
        l=n-1;
        LG_poly=LG_poly+(-1)^l*((factorial(P+abs(L)))/((factorial(P-l))*(factorial(abs(L)+l))*(factorial(l)))).*X.^l;
    end
    E1=wz^(-1).*(sqrt(2)*sqrt(r.^2)/wz).^abs(L).*LG_poly.*exp(-(r.^2)./wz^2);
    E2=exp((-1i*k0*(r.^2)*z)/(2*(z^2+zR^2)));
    E3=exp(-1i.*(2.*P+abs(L)+1).*atan(z/zR));
    LG_OAM=Clp.*E1.*E2.*E3.*exp(-1i.*L.*phai);
end

2.1.2 文件"beam_parameter.m"

function [lambda,k,z,w0,x,y] = beam_parameter(N)
    lambda = 0.532e-6;
    k = 2 * pi / lambda; %波数
    z = 0; 
    w0 = 0.005;
    T0 = 4;
    R1 = T0 * w0; %范围
    x = linspace(-R1, R1, N);
    y = linspace(-R1, R1, N);
end

2.1.3 示例

clc; clear;
N = 1000;

%%产生OAM涡旋光束
[lambda,k,z,w0,x,y] = beam_parameter(N);
beam1 = lg_oam(-5,w0,0,lambda,x,y);
beam2 = lg_oam(-3,w0,0,lambda,x,y);
beam3 = lg_oam(2,w0,0,lambda,x,y);
beam4 = lg_oam(4,w0,0,lambda,x,y);
beam = beam1 + beam2 + beam3 + beam4;

%%显示光强图
figure();
imagesc(x,y,abs(beam).^2);
colormap hot;
axis off;
title('OAM光束光强图');

2.2 数值仿真螺旋功率谱-文件"spectrum.m"

function result = spectrum(beam,w0,z,lambda,x,y)
    res = zeros(1, 17);
    for mode=-8:8
        beam0 = lg_oam(mode,w0,0,lambda,x,y);
        beam_abs = beam.*conj(beam0);
        res(1,mode+9) = abs(sum(beam_abs(:)));
    end
    all_sum = sum(res(1,:));
    result = res/all_sum;
end

2.3 利用螺旋功率谱检测OAM叠加态涡旋光束

clc; clear;
N = 1000;

%%产生OAM涡旋光束
[lambda,k,z,w0,x,y] = beam_parameter(N);
beam1 = lg_oam(-5,w0,0,lambda,x,y); %OAM模式值l=-5, 径向指数p=0
beam2 = lg_oam(-3,w0,0,lambda,x,y); %OAM模式值l=-3, 径向指数p=0
beam3 = lg_oam(2,w0,0,lambda,x,y); %OAM模式值l=2, 径向指数p=0
beam4 = lg_oam(4,w0,0,lambda,x,y); %OAM模式值l=4, 径向指数p=0
beam = beam1 + beam2 + beam3 + beam4;

%%得到叠加态涡旋光束的螺旋功率谱
result = spectrum(beam,w0,z,lambda,x,y);

%%显示图像
figure();
m = -8:8;
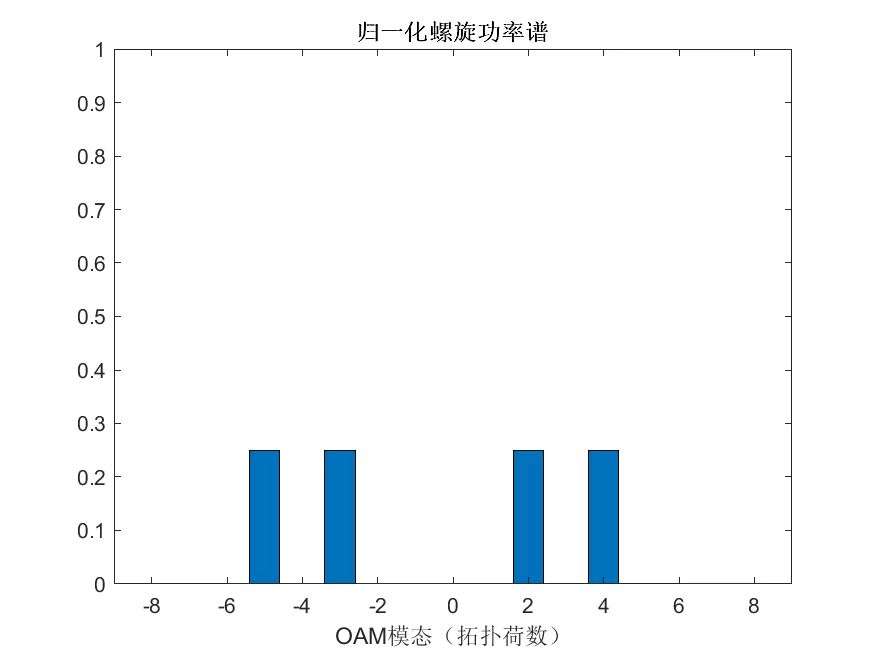
bar(m,result);
title('归一化螺旋功率谱');
xlabel('OAM模态（拓扑荷数）');
axis([-9,9,0,1]);