常见的OAM涡旋光束--MATLAB仿真

1.常见4种光束比较

光束 优点
拉盖尔-高斯(LG)光束 具有高斯光束的特点且易在实验室进行制备，是一种最常用的涡旋光源
贝塞尔-高斯(BG)光束 具有无衍射特性、方向性好等优点
完美涡旋(PV)光束 具有稳定的结构、强化的光场局域性等优点
厄米-高斯(HG)光束 具有非常纯净的横向模式和良好的聚焦特性

2.拉盖尔-高斯(LG)光束

2.1 理论

拉盖尔-高斯光束（LG）的复振幅表达式:

\[U_{pl}^{LG}(r,\phi,z)=A_{LG}\times \sqrt{\frac{2P!}{\pi (p+|l|)!}}\frac{1}{w(z)}\left[\frac{r\sqrt{2}}{w(z)}\right]^{|l|}L_{p}^{|l|}\left[\frac{2r^2}{w^2(z)}\right]\times exp\left[\frac{-r^2}{w^2(z)}\right]\times exp\left[\frac{-ikr^2z}{2(z^2+z_R^2)}\right]exp\left[i(2p+|l|+1)tan^{-1}\frac{z}{z_R}\right]exp(-il\phi) \]

其中\((r,\phi,z)\)为柱坐标参数，\(A_{LG}\)为振幅，\(l\)为OAM模式值，表示空间相位的变化，\(p\)为径向指数，\(w(z)=w_0\sqrt{1+(z/z_R)^2}\)是LG光束在\(z\)处的束腰半径，\(w_0\)是基模高斯光束在\(z=0\)处的束腰半径，\(w_0=\pi w_0^2/\lambda\)是瑞丽距离，\(\lambda\)为光束波长，\(k=2\pi /\lambda\)是光束的波数，\((2p+|l|+1)tan^{-1}\frac{z}{z_R}\)是Gouy相位，\(L_{p}^{|l|}\)为归一化的拉盖尔多项式，其表达式为：

\[L_{p}^{|l|}=(-1)^{|l|}\frac{d^{|l|}}{dx^{|l|}}L_{p+|l|}(x) \]

2.2 仿真

2.2.1 函数"lg_oam.m"

function [LG_OAM]=lg_oam(L,w0,P, lamda, x,y)
    % x=linspace(-T*w0,T*w0,N);
    % y=linspace(-T*w0,T*w0,N);
    [px,py]=meshgrid(x,y);
    r=sqrt(px.^2+py.^2);
    phai=atan2(py,px);
    z=0;

    k0=2*pi./lamda;
    zR=pi*w0^2/lamda;
    wz=w0.*sqrt((z.^2+zR.^2)./zR.^2);
    Clp=sqrt(2.*factorial(P)./(pi.*factorial(P+abs(L))));
    X=2*(r.^2)./wz^2;
    LG_poly=0;

    for n=1:P+1
        l=n-1;
        LG_poly=LG_poly+(-1)^l*((factorial(P+abs(L)))/((factorial(P-l))*(factorial(abs(L)+l))*(factorial(l)))).*X.^l;
    end

    E1=wz^(-1).*(sqrt(2)*sqrt(r.^2)/wz).^abs(L).*LG_poly.*exp(-(r.^2)./wz^2);
    E2=exp((-1i*k0*(r.^2)*z)/(2*(z^2+zR^2)));
    E3=exp(-1i.*(2.*P+abs(L)+1).*atan(z/zR));
    LG_OAM=Clp.*E1.*E2.*E3.*exp(-1i.*L.*phai); 
end

2.2.2 函数"beam_parameter.m"

function [lambda,k,z,w0,x,y] = beam_parameter(N)
    lambda = 0.532e-6;   %波长
    k = 2 * pi / lambda; %波数
    z = 0; 
    w0 = 0.005;          %束腰半径
    T0 = 4;
    R1 = T0 * w0;        %范围
    x = linspace(-R1, R1, N);
    y = linspace(-R1, R1, N);
end

2.2.3 示例

clc; clear;
N = 1000;
[lambda,k,z,w0,x,y] = beam_parameter(N);
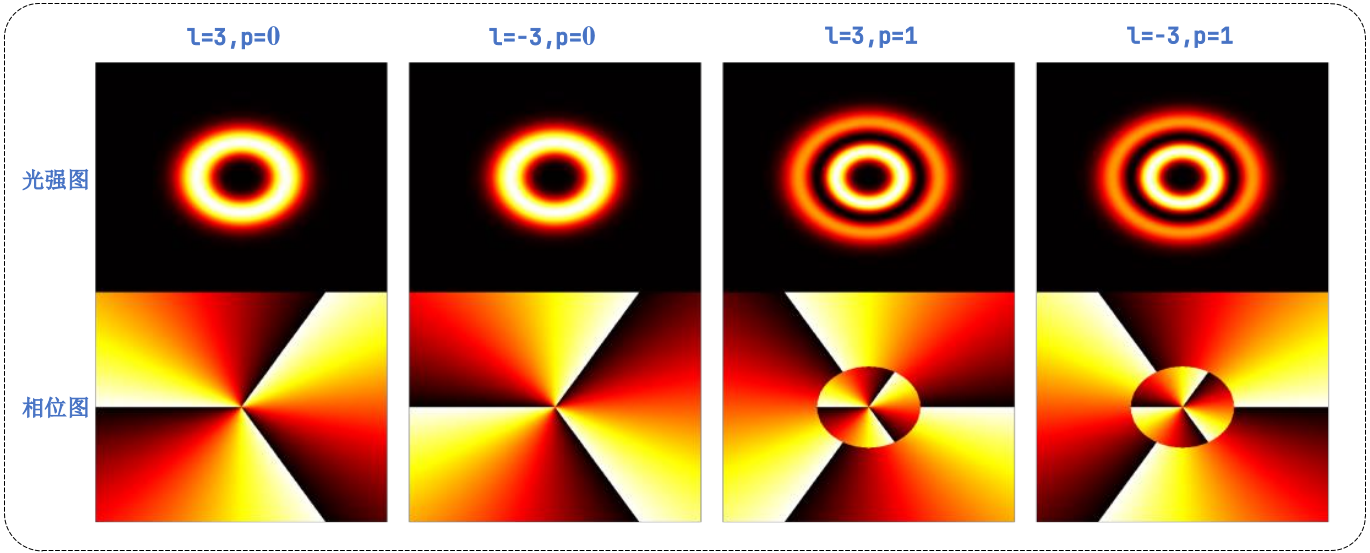
l = 3; p = 1;
beam = lg_oam(l,w0,p, lambda, x,y);

figure();
imagesc(x,y,abs(beam).^2);
colormap hot;
axis off;
title('光强图');

figure();
imagesc(x,y,angle(beam));
colormap hot;
axis off;
title('相位图');

v2-69e941f8d36c1035eb7dc8f1ce84f048_1440w

3.贝塞尔-高斯(BG)光束

3.1 理论

1987 年，Durnin 等人发现了具有无衍射特性贝塞尔光束, 理想状态下的贝塞尔-高斯光束可以被描述为:

\[E_{BG}(r,\theta)=AJ_l(k_r r)exp(-\frac{r^2}{w_0^2})exp(il\theta) \]

式中，\((r,\theta,z)\)为极坐标，\(l\)为拓扑荷数及贝塞尔函数的阶数，\(k_r\)为径向波数，\(w_0\)为束腰半径。

3.2 仿真

clc; clear all; close all;
N = 200;
lambda = 1064e-6;                 %波长1064nm
row = linspace(-1,1,N); col = linspace(-1,1,N);
[x,y] = meshgrid(row,col);
[theta,r] = cart2pol(x,y);
w = 3;                            %高斯光束束腰宽度
k = 2*pi/lambda;                  %波数
k_r = 20;                         %径向波矢 - 常量
k_z = sqrt(k^2-k_r^2);            %轴向波矢
z = 0;
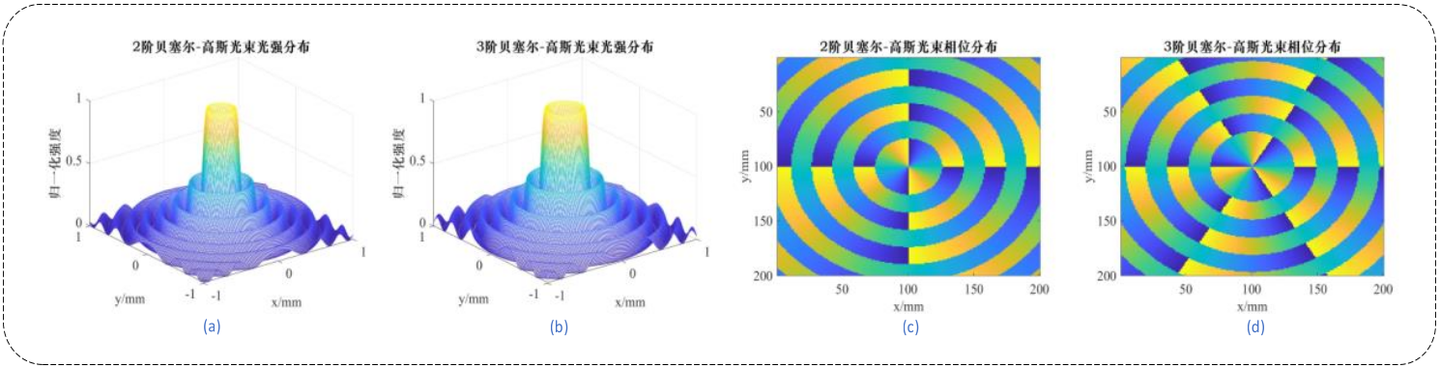
n = 3;                            %贝塞尔函数阶数n = 3
E = besselj(n,k_r*r).*exp(-r.^2/w^2).*exp(1i*k_z*z).*exp(1i*n*theta);

I1 = angle(E);
figure();
imagesc(I1);
set(gca,'fontname','times new roman','fontsize',16);
title([num2str(n),'阶贝塞尔-高斯光束 相位图'],'fontname','华文中宋','fontsize',16);
xlabel('x/mm','fontname','times new roman','fontsize',16);
ylabel('y/mm','fontname','times new roman','fontsize',16);

I2 = E.*conj(E);
I2 = I2/max(max(I2));             %归一化
figure();
mesh(x,y,I2)
set(gca,'fontname','times new roman','fontsize',16);
title([num2str(n),'阶贝塞尔-高斯光束'],'fontname','华文中宋','fontsize',16);
xlabel('x/mm','fontname','times new roman','fontsize',16);
ylabel('y/mm','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);

v2-36b16a5c17482dd94e33beddae21dd4d_1440w

4.完美涡旋(PV)光束

4.1 理论

目前完美涡旋光束的生成方法包括锥透镜函数法、贝塞尔光束傅里叶透镜变换法. 这里我们选择使用贝塞尔光束傅里叶透镜变换法，利用狄拉克函数可以把该光束的复振幅表示为：

\[E(r,\theta)=\frac{i^{l-1}}{k_r}\delta(r-k_rf/k)exp(il\theta) \]

其中\((r,\theta)\)是极坐标下的坐标点, \(k_r\)为径向波数,\(l\)为OAM模式值, \(\delta(r)\)为狄拉克函数, \(f\)为透镜的焦距。

4.2 仿真

clc;clear all;close all;

%% 振幅光学相位元件产生完美涡旋光场
N = 300;
row = linspace(-1.5e-6,1.5e-6,N);   
col = linspace(-1.5e-6,1.5e-6,N);
[x,y] = meshgrid(row,col);
[phi,rho] = cart2pol(x,y);
lambda = 632e-9;    %波长632nm
k = 2*pi/lambda;    %波数
f = 0.5;            %透镜焦距0.5m
R = 0.5;            %圆孔光阑半径0.3m
X = k*rho/f;
alpha = 20;         %径向波矢 - 常数

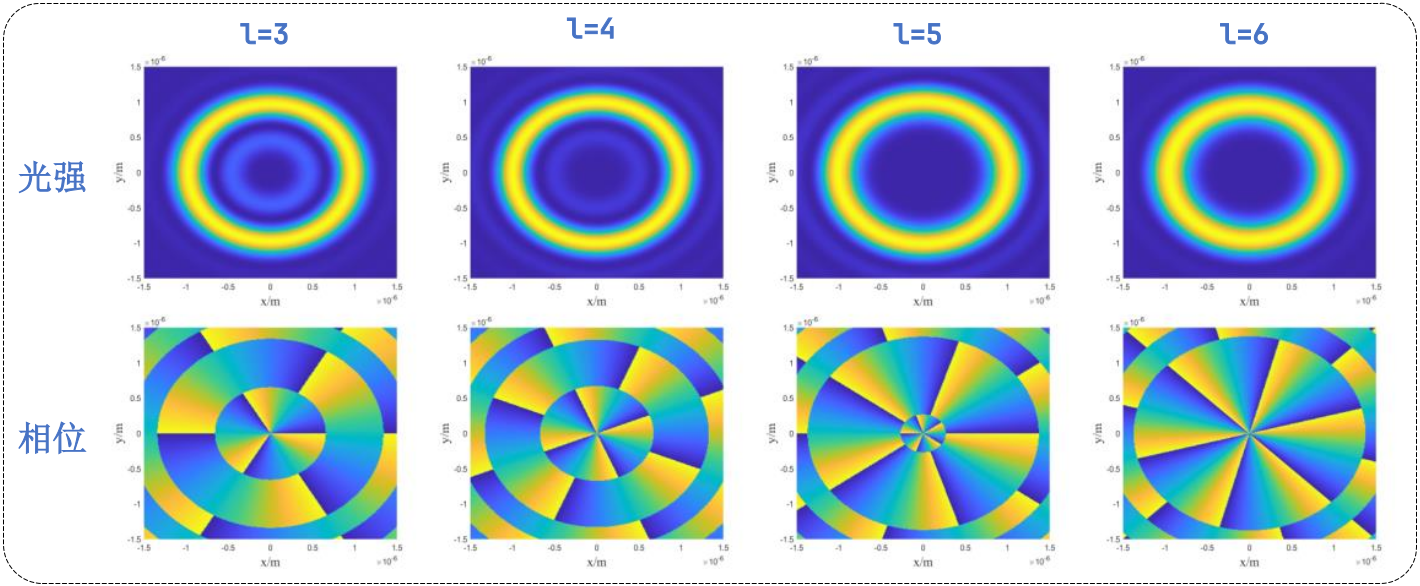
m = 4; %阶数
E1 = (-1i)^(m+1)*(k*R/f)*exp(1i*m*phi).*...
            ((alpha*besselj(m+1,alpha*R)*besselj(m,X*R)-X.*besselj(m,alpha*R).*besselj(m+1,X*R))./(alpha^2-X.^2));  

figure();
I1 = angle(E1);
h1 = pcolor(x,y,I1);
set(h1,'edgecolor','none','facecolor','interp');
title(['m = ',num2str(m) '相位图']);
xlabel('x/m','fontname','times new roman','fontsize',16);
ylabel('y/m','fontname','times new roman','fontsize',16);
colorbar off;

figure();
I2 = E1.*conj(E1); 
I2 = I2/max(max(I2));
mesh(x,y,I2)
set(gca,'fontname','times new roman','fontsize',16);
title(['m = ',num2str(m)],'fontname','华文中宋','fontsize',16);
xlabel('x/m','fontname','times new roman','fontsize',16);
ylabel('y/m','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);

v2-ecdf794d47ef2f314f1100164e328184_1440w

5.厄米-高斯(HG)光束

5.1 理论

厄米-高斯光束（HG）在其传播方向上的光场表达式为：

\[E_{nm}^{HG}(r,\phi,z)=A_{HG}\frac{1}{\sqrt{2^mm!}}\frac{1}{\sqrt{2^nn!}}\sqrt{\frac{2}{\pi}}\frac{1}{w(z)}H_m\left[\frac{\sqrt{2}y}{w(z)}\right]H_n\left[\frac{\sqrt{2}y}{w(z)}\right]\times exp\left[-\frac{x^2+y^2}{w(z)}\right]exp\left[-\frac{ik(x^2+y^2)}{2(z^2+z_R^2)}\right]exp\left[i(m+n+1)tan^{-1}\frac{z}{z_R}\right] \]

其中\(H_m(\cdot )\)是n阶Hermite多项式。

5.2 仿真

clear; close all;

x=[-5:0.1:5].*1e-3;            % 设定腔镜坐标
lambda=632.8e-9;               % 设定激光器出光频率
L=10;                          % 设定激光腔腔长
X=x.*sqrt(2*pi./(lambda.*L)); 
Y= X;
[X1,Y1]=meshgrid(X,X);         % 获取X和Y的坐标矩阵

% 设定厄米特函数，n和m只从0取到2
% 绘制三维
H0X=1;                          
H1X=2.*X1;
H2X=4.*X1.^2-2;
H0Y=1;
H1Y=2.*Y1;
H2Y=4.*Y1.^2-2;

% 三维公式
FX0=H0X.*exp(-X1.^2-2);         % 生成厄米特——高斯函数
FX1=H1X.*exp(-X1.^2-2);
FX2=H2X.*exp(-X1.^2-2);

FY0=H0Y.*exp(-Y1.^2-2);
FY1=H1Y.*exp(-Y1.^2-2);
FY2=H2Y.*exp(-Y1.^2-2);

% 二维公式
H0X1=1;                          
H1X1=2.*X;
H2X1=4.*X.^2-2;
H0Y1=1;
H1Y1=2.*Y;
H2Y1=4.*Y.^2-2;

F0X=H0X1.*exp(-X.^2-2);         % 生成厄米特——高斯函数
F1X=H1X1.*exp(-X.^2-2);
F2X=H2X1.*exp(-X.^2-2);

F0Y=H0Y1.*exp(-Y.^2-2);
F1Y=H1Y1.*exp(-Y.^2-2);
F2Y=H2Y1.*exp(-Y.^2-2);

% mode = 0
I2=FX0.^2.*FY0.^2;              % 考虑X和Y两个方向分布
figure();
I2 = I2/max(max(I2));
surf(X1,Y1,I2);
xlabel('x/m','fontname','times new roman','fontsize',16);
ylabel('y/m','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
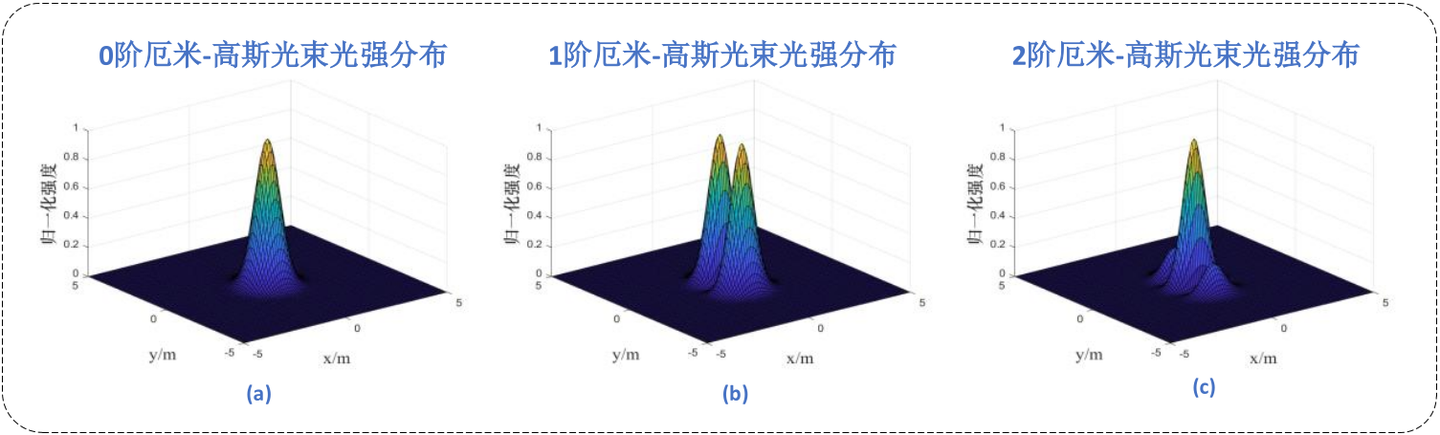
title('厄米—高斯光束光强分布,m=0','fontname','华文中宋','fontsize',16);

% mode = 1
I2=FX0.^2.*FY1.^2;              % 考虑X和Y两个方向分布
figure();
I2 = I2/max(max(I2));
surf(X1,Y1,I2);
xlabel('x/m','fontname','times new roman','fontsize',16);
ylabel('y/m','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
title('厄米—高斯光束光强分布,m=1','fontname','华文中宋','fontsize',16);

% mode = 2
I2=FX0.^2.*FY2.^2;              % 考虑X和Y两个方向分布
figure();
I2 = I2/max(max(I2));
surf(X1,Y1,I2);
xlabel('x/m','fontname','times new roman','fontsize',16);
ylabel('y/m','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
title('厄米—高斯光束光强分布,m=2','fontname','华文中宋','fontsize',16);

v2-b4be7480d52011dfb8f3f5ef2debca59_1440w

6.Reference

  • DURNIN J, MICELI J, EBERLY J H. Comparison of Bessel and Gaussian beams[J]. Optics letters, 1988, 13(2): 79-80.
  • OSTROVSKY A S, RICKENSTORFF-PARRAO C, ARRIZÓN V. Generation of the “perfect” optical vortex using a liquid-crystal spatial light modulator[J]. Optics letters, 2013, 38(4): 534-536.
  • VAITY P, RUSCH L. Perfect vortex beam: Fourier transformation of a Bessel beam[J]. Optics letters, 2015, 40(4): 597-600.
  • 李霞. 厄米-高斯光束和优美厄米-高斯光束的艾里变换研究[D]. 浙江农林大学, 2022.
posted on 2026-02-01 15:52  curme_miller  阅读(0)  评论(0)    收藏  举报
博客园  ©  2004-2026
浙公网安备 33010602011771号 浙ICP备2021040463号-3