#Deeplearning#人工智能导论学习笔记
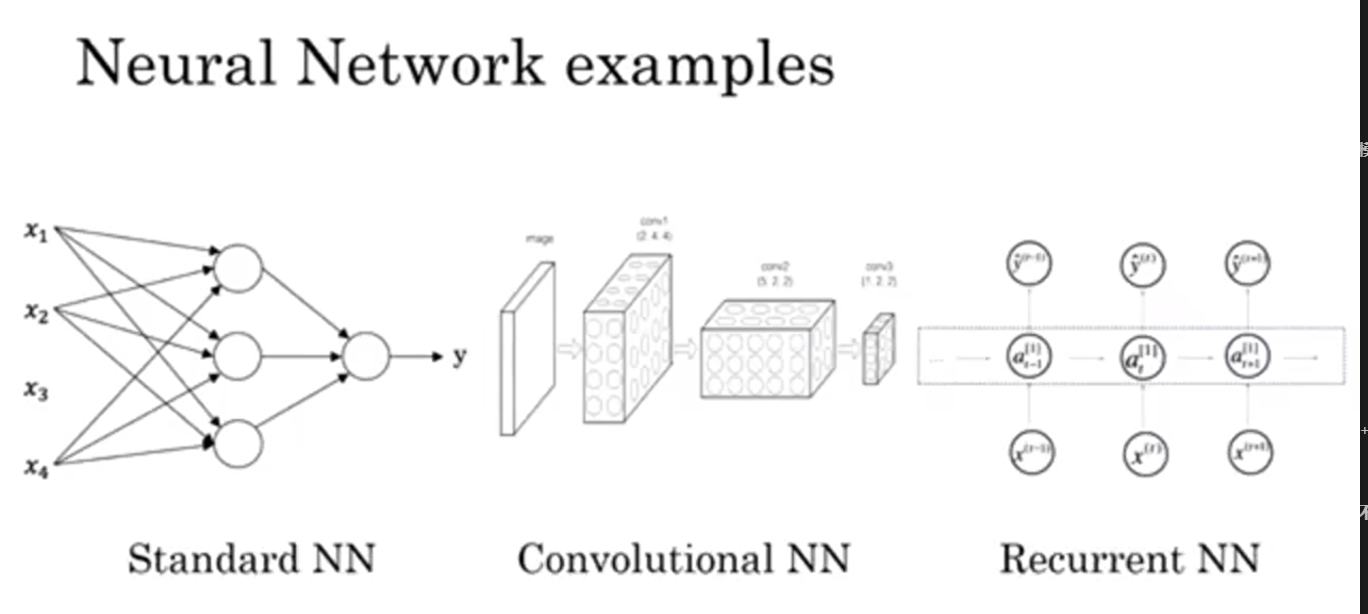
什么是神经网络？
SNN用于回归预测数值，房价或在线广告投放等等
CNN用于图像处理
RNN用于音频和自然语言处理
RNNS用于大文本数据处理
自动驾驶则是多种神经网络组合
配套练习：https://hekuan.blog.csdn.net/article/details/79862336
神经网络基础和深度学习
深度学习指的就是训练神经网络
Relu：修正线性单元（修正指的是不取小于0的值）
输入需要分给每一个神经元，这个过程就叫全连接
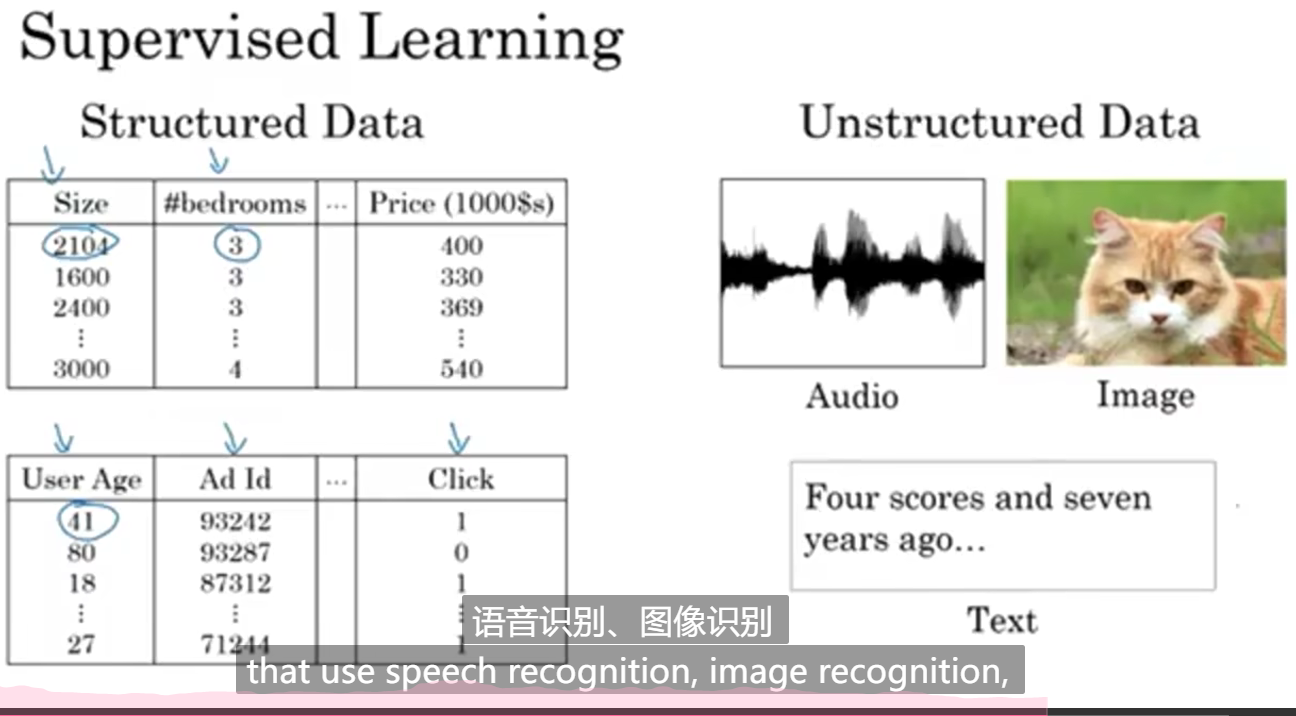
监督学习（Supervised Learning）
需要真实的数据标签，即俗称的“拉框”等等由人工不断干预的
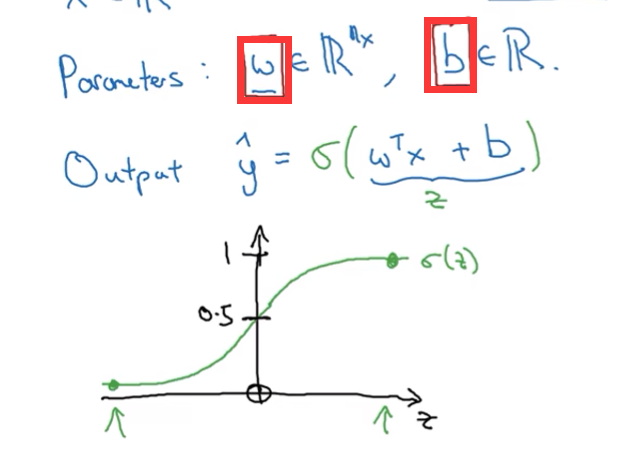
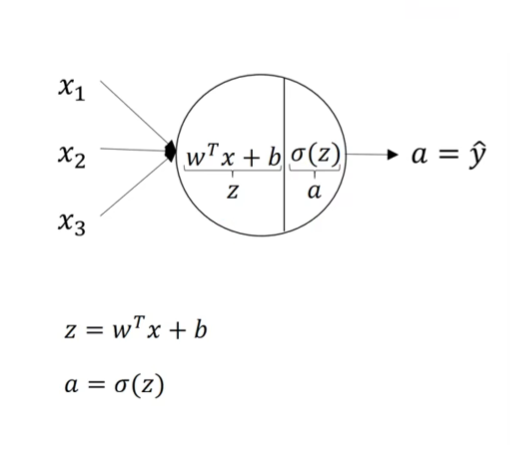
这是一个学习算法，已知输入一个图像特征向量x，输出y是一个概率，预测这个特征符合这个类的概率是多少，这需要在乘权重参数矩阵W后进sigmoid函数变换，使其值在0到1之间
结构化数据：每个数据都有清晰的定义
非结构化数据：图像、音频、文字等等
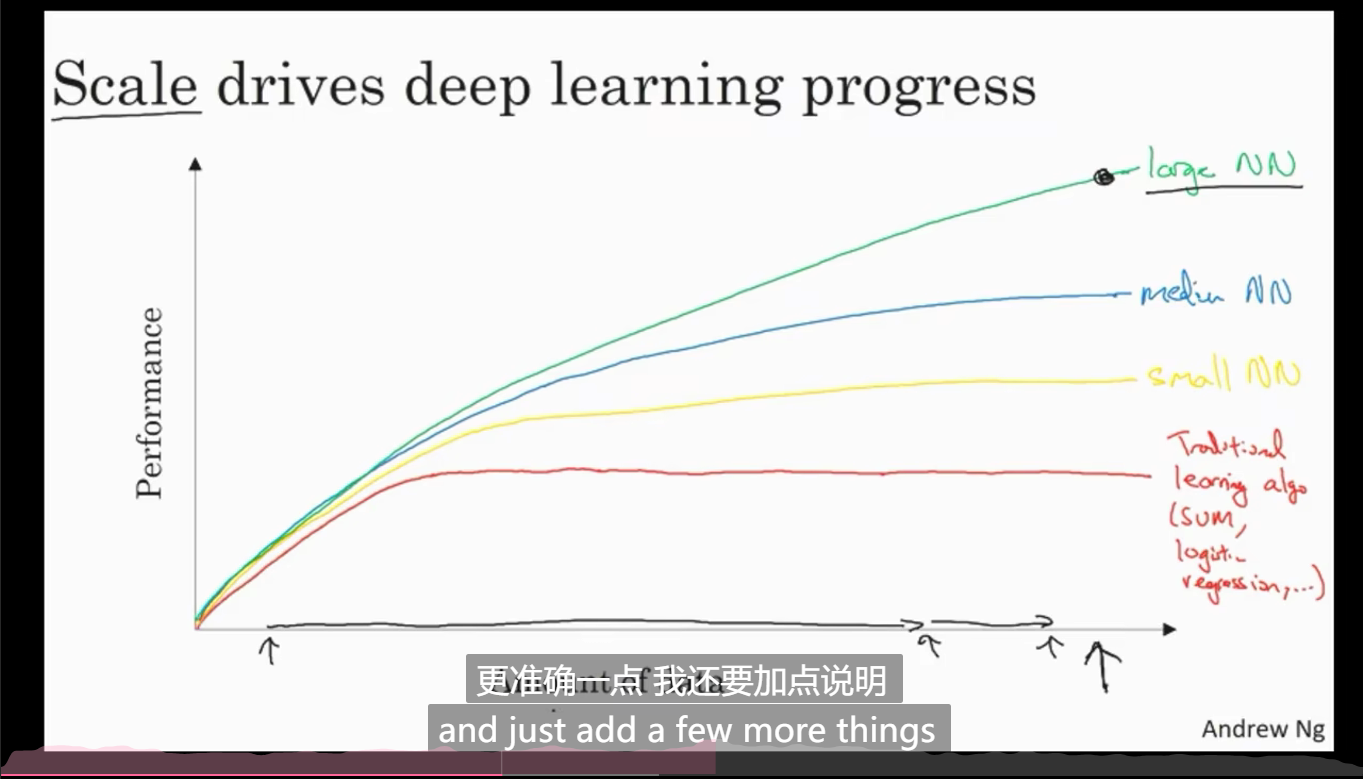
上图中，x周代表训练集大学或神经网络大小，y轴代表模型性能
规模能够显著影响模型的表现，想获得良好表现的条件不仅仅是模型规模大，训练集规模也要大
logistic回归算法
本节后面所有的讲解都是 用logistic回归作为背景的
该算法用于二分分类
提取图像的特征矩阵作为输入x，模型需要判断这个x是不是某个东西，是就输出1，不是就输出0，输出标签用y代表
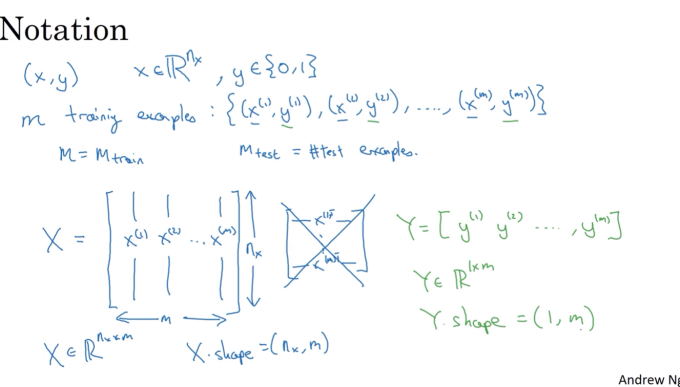
输入标签x和输出标签y的矩阵表示，都用行堆叠，如果一个样本的维度是n，那么训而输出标签只有0或1，只需要按行排列在行矩阵里即可
m表示训练集的规模
回归模型需要的参数是权重矩阵w的常数b，因此学习的是w和b
详细：
前提是必须是二分类问题，非0即1
前面两个表达式可以合并为一个：
符号意义参照表及背景
下面的介绍以logistic回归函数为例，提取特征为2个或n个，样本个数为1或m
| a | W | z | y | y帽 | x | b | L或L(a，b) | da | m | n | i | J |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sigmoid(z) | 权重参数（矩阵、向量） | 预测值（需要经过sigmoid激活函数变换） | 数据真实结果标签 | 模型预测结果标签（给定x输入下y=1的概率） | 输入数据 | 常数（矩阵，向量） | 损失函数 | L对a的导数（链式法则求导） | 样本数 | 特征数 | 样本编号 | 全局成本函数 |
y帽的条件概率表达如下
损失函数Loss function
用于衡量预测输出y1和实际值y相差多少，它衡量了在单个训练样本上的表现
成本函数Cost function
用于衡量W和b在全体训练样本上的表现
其凸函数的性质决定了它具有全局最优解，而非多个局部最优解，因此选用凸函数作为成本函数
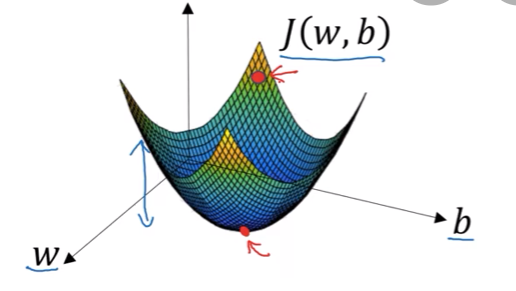
其大致操作是，在一次迭代中朝着下降最快（最陡）的方向走一步
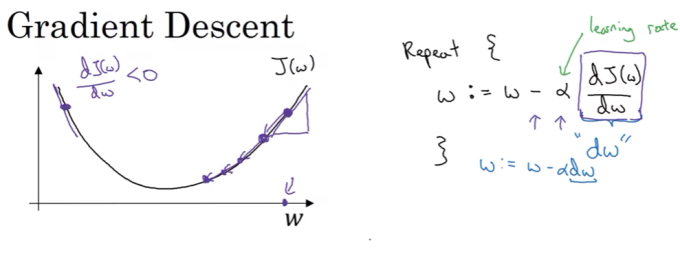
梯度下降法
寻找使得cost function最小的W和b
1.对单一样本
让Cost函数始终沿着最“陡”的路径向下移动
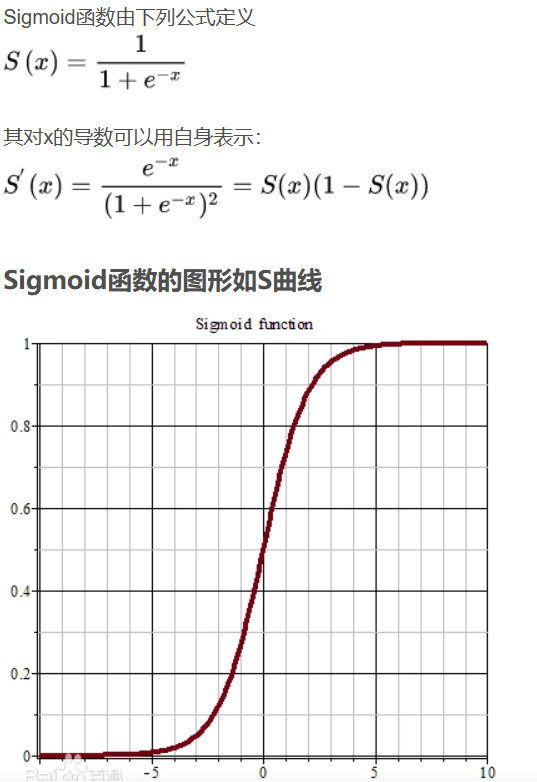
权重更新算法：W = W - a*dw
a是学习率，dw是成本函数对w的导数
对b也是同样的方法，通过梯度削减b
涉及到多个变量需要链式求导法则
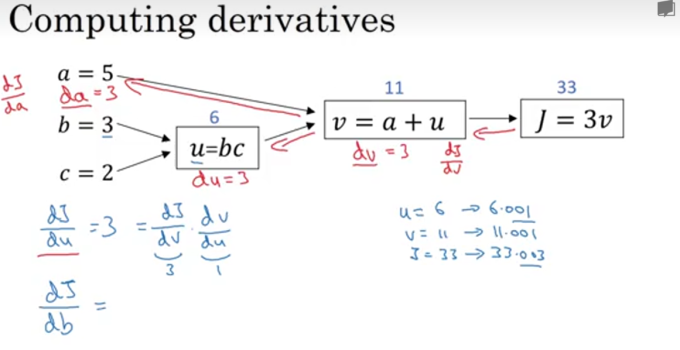
上图中，J对a求导需要经过dJ/dv * dv/da
2.对m个训练样本（训练集）
全局成本函数：各项损失函数之和求平均
写成代码如下图
注意，这里是代码，并不是表示数学关系，dz，dw1，dw2，dwn...（一共n个特征）和db都需要累加，在for循环结束后，都要除以样本个数m，这里只有w1和w2两个权重参数矩阵，也就是说只会提取出两个特征，当有很多特征时，还需要再写一个循环将w1、w2...一直到wn的n个特征都做一次累加
实际上，显式for循环的效率非常低，难以高效处理大量数据，下面会介绍一种向量化的算法，避免使用for循环
最后再用下面的公式，完成一次迭代
导数及链式法则在反向传播中的应用
以logistic回归函数为例
训练目的：不断完善W和b的值，最小化损失函数L（a，y）
注：这里log（a）指的就是以e为底（ln（a））
求导过程参见求导公式表
注：
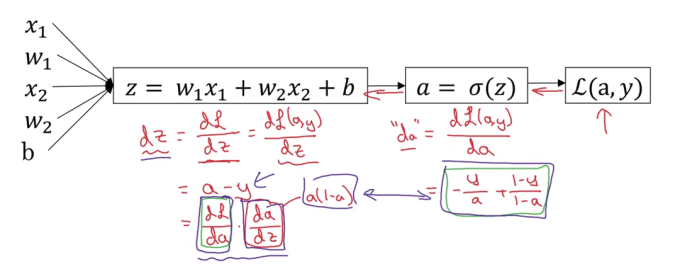
- dL和d(a,y)表达的意思是一样的
- a是sigmoid函数，求导结果为a(1-a)
- 在编码实现时（Python），对w1的导数直接写成dw1，默认就是最终的损失函数L对w1求导，因为损失函数是我们最关心的最终结果
dw1用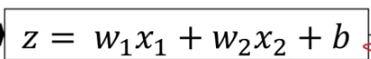 
*计算得到，在上图的左下角有写“ dw1 ” = x1dz ；这里的dz也不是数学中的dz，而是L对z的导数 ***
一次迭代中的更新方法为
注：alpha是学习率
向量化（vectorization）
以Python为例
两个大维度向量（100w）a和b用np.dot(a，b)计算，效率远高于用for将两个对于相乘，其原因是Python的内置函数库（numpy）支持并行，用基础函数库中专门用于向量计算的函数能够充分利用并行
向量化的运算耗时平均2.5ms，for循环平均耗时480ms
因此，能不显式用for循环的地方必须不用for循环，而是用库中函数或者用其他方法计算循环！！
所以对代码进行这样的改进：
原本的三个for循环（红色框）都可以用np.dot(a,b)代替，效率大幅提高
下面介绍如何将控制样本的for循环也替换掉，实现完全不使用显式for循环
前向传播计算过程表示如下
Python有一个特性，在矩阵后加常数，常数会自动扩展成一个常数矩阵，使其能和矩阵进行运算，同样的，Python也能高效做矩阵运算，两个矩阵可以直接相加减，不需要for循环
因此之前的代码可以用下面的向量运算全部表示
广播技术
例子：Python在面对矩阵加常数时，会把常数扩展成对应维度的矩阵，同样对于m × n的矩阵加1×n的矩阵时，Python也会把1×n的矩阵扩展成m × n的矩阵，然后对应元素相加
数据结构应该使用向量，即使它只有一行
a = np.random.rand(5,1);
a = np.random.rand(5);
上面两行代码的区别是，第一个a是列向量，第二个a是一个秩为1的数组，我们应该用第一个，因为向量的外积才是矩阵
必要时通过加入assert(a.shape == (5,1))确保数据结构是形状为（5,1）的列向量，这个函数执行非常快，几乎不会影响效率
第一周结束！
神经网络
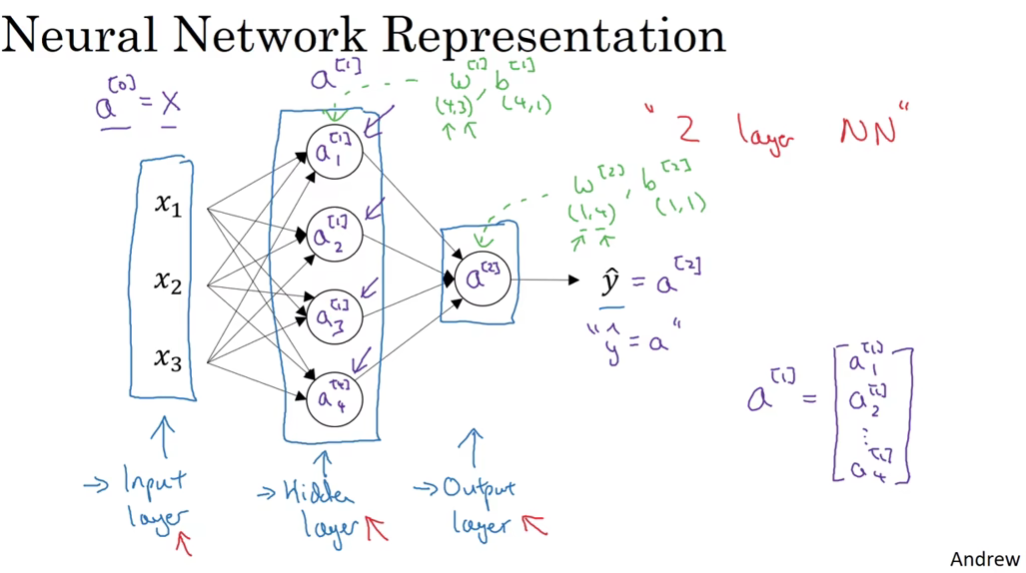
[1]代表和第1层相关的量，右下角标表示特征/神经元编号
带角标的是和某个神经元相关
不带角标是这一层某个量组成的向量
叠加角标的顺序是：[1] (i) ；表示第1层第i个训练样本
大写字母表示对全体训练样本
小写字母表示对单一训练样本
最简单的神经网络结构图（只有一个隐层，单一训练样本）
输入层、隐藏层、输出层共三层，但一般习惯上不认为输入层是一个标准层，因此这个网络在许多论文和课程中也称为双层神经网络
一个神经元中完成的计算如上图所示，和logistic回归很相似
注意：这里x1、x2和x3并不是一个数字，而是一个特征,是一个具有一定维度的向量
经过一次计算后得到的a称为激活值，作为下一次计算的输入，其上标代表它由哪层产出，有时候也把输入x看做是a[0],因此所有 x 都可以用 a[0] 代替（X用A代替），代替后会增加一个角标[0]
矩阵乘法规则：左矩阵列数 = 右矩阵行数
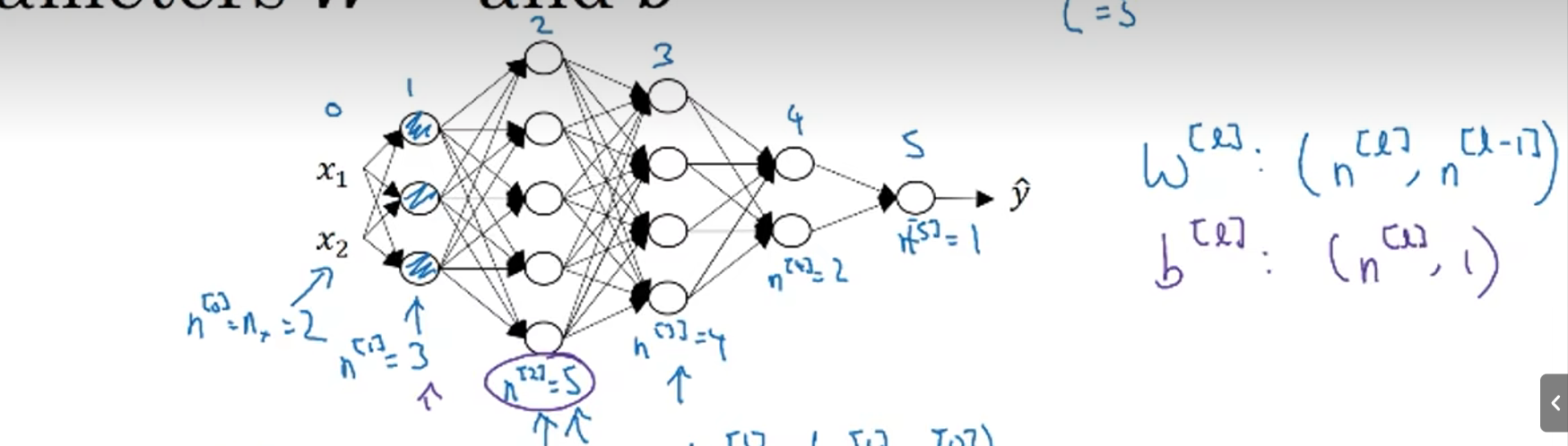
维度公式：
A×B * B×C = A × C
维度形式（可用于检验每一层的维度是否正确）：
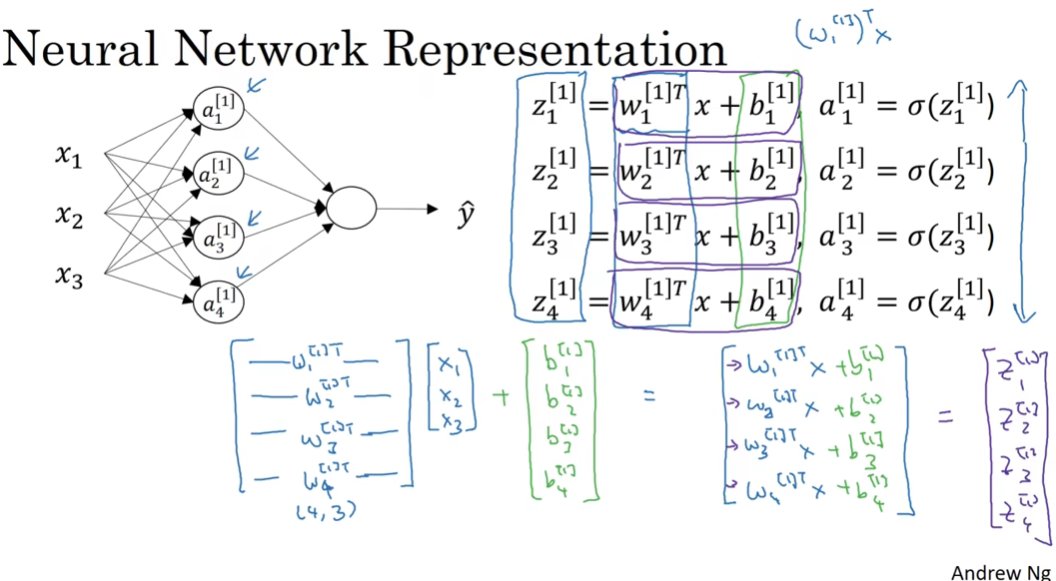
将神经元中的计算向量化方法如下图：
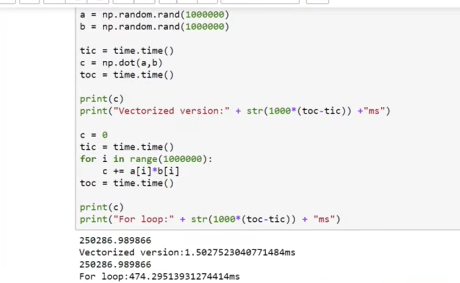
权重参数矩阵W是转置后按行堆叠的矩阵，维度为4x3 （4个神经元、3个特征输入，每个元素还有N个值），特征x为按列堆叠的矩阵，维度为3x1（3个特征,每个特征具有1个值）
最后一层（输出层）的W是1x4的，b是1x1的，因为这里最终要输出一个数字
对整个训练样本向量化如下图
整个训练样本构成的向量用大写表示，X、Z和A都进行了向量化
横向移动是遍历训练样本，纵向移动是遍历神经元
下面这张图，比较详细的演示了每一步计算后，形成的矩阵的样子
激活函数
影响学习速度，其利弊主要指标是导数和0的距离，导数约接近0，学习速度越慢
sigmoid函数几乎完全被tanh（双曲正切函数）碾压，因为它是sigmoid的平移版本，将中心点移到0了，因此绝大多数情况下不用sigmoid，除了二元分类，因为我们希望输出0到1之间的数
也可以在隐层之间用其他激活函数，最后的输出层用sigmoid，为此需要给函数做下标，标记方式为g[1] (z)，[1]代表第一层
事实上，这两个函数在z很大时表现都不好（斜率趋近于0，反向传播出现梯度消失），最佳的选择是修正线性单元ReLU
ReLU(z) = max(0,z)
变体（效果有可能更好）：Leaky ReLU(z) = max(0.01z,z)
值得一提的是，ReLU在z = 0 处并没有定义，但是这个概率很小，而且可以在z = 0时给导数赋值0或1
激活函数总结
输出0或1（二元分类）：输出层用sigmoid，其他层都用ReLU
能不能不用激活函数，或者用线性激活函数？
不能！，不用激活函数或者用线性激活函数，无论你有多少隐藏层，模型复杂度和没有隐藏层一样，因为层与层之间只是线性运算的叠加，线性隐层一点用都没有
网络构建实践
正则化：避免过拟合
在回归logistic模型中，常用的正则化为L2正则化：一个比例系数×权重w的欧几里得范数（从w1至wnx累加平方和）
在神经网络中，进行L2正则化的方法是在全局成本函数J后加一个范数，简单来说就是比例系数 乘以 权重参数矩阵W的所有元素的平方和
学习公式后面也加上正则项 ，dw[l]要在原来的基础上（from backprop）加上正则项（第一行）。w的学习公式编程第二行所示
w学习公式展开如下
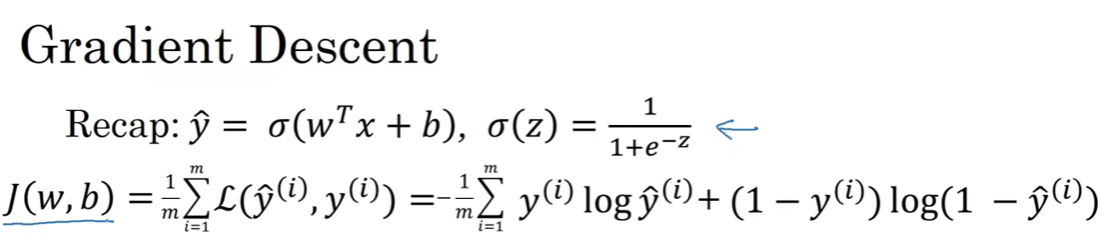
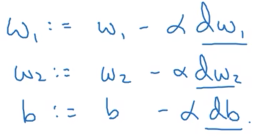
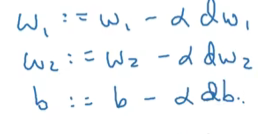
浙公网安备 33010602011771号