图的基本概念

图 是由顶点集合和顶点间的关系集合组成的一种数据结构，通常表示为 G = (V,E) 。其中V表示顶点集合，E表示顶点之间的关系集合。

下面是几种我们常见的图。

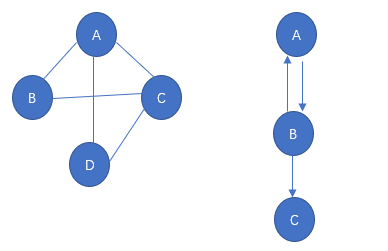
有向图 是指顶点对<x,y>是有序的，对于有序图来说<x,y>与<y,x>是两条不同的边。有向图中的边又称为弧。

无向图 中顶点(x,y)是指x,y顶点关联的边，这条边是没有方向的。上图第一个图就是无向图，图二就是有向图。

完全图 对于无向图来说，是指在图中任意两个顶点之间有且仅有一条边，也就是说n个顶点的无向图，有n*(n-1)/2条边；

　　对于有向图来说，是指图中任意两个顶点之间有且仅有两条方向相反的边，也就是说n个顶点的有向图，有n*(n-1)条边。

邻接顶点 对于无向图来说，如果顶点A、B之间存在边（A,B）则称A的邻接顶点有B，B的邻接顶点有A，如上图一，A的邻接顶点就有B、C、D。

　　对于有向图来说，如果顶点A、B之间存在弧<A,B>，就称A邻接到B，B领结自A。

顶点的度 是指与该顶点关联的边的数目。有向图中顶点v的度TD(v) = 入度+出度。 入度是指以v为终点的弧的条数，出度是指以v为起始点的弧的条数。

权 有些图的边附带有数据信息，这些附带的数据信息就称为权。带权的图又称为网络或网。

路径长度 对于不带权的图，路径长度就是指该路径上边的条数，对于带权的图，路径长度就是指该路径上所有权值的总和。

连通图 在无向图中，如果顶点A B之间存在路径，则称A B是连通的。如果图中任意一对顶点都是连通的，则称该图是连通图。

强连通图 在有向图中，如果任意一对顶点之间都存在路径，则称图是强连通图。

　　如下图。图一就是连通图，图二就是强连通图。

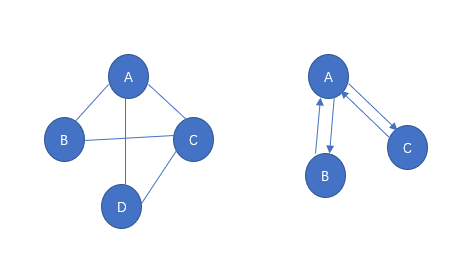
生成树 一个连通图的最小连通子图称为该图的生成树。有n个顶点的连通图的生成树有n个顶点，n-1条边。