红黑树

红黑树定义和性质

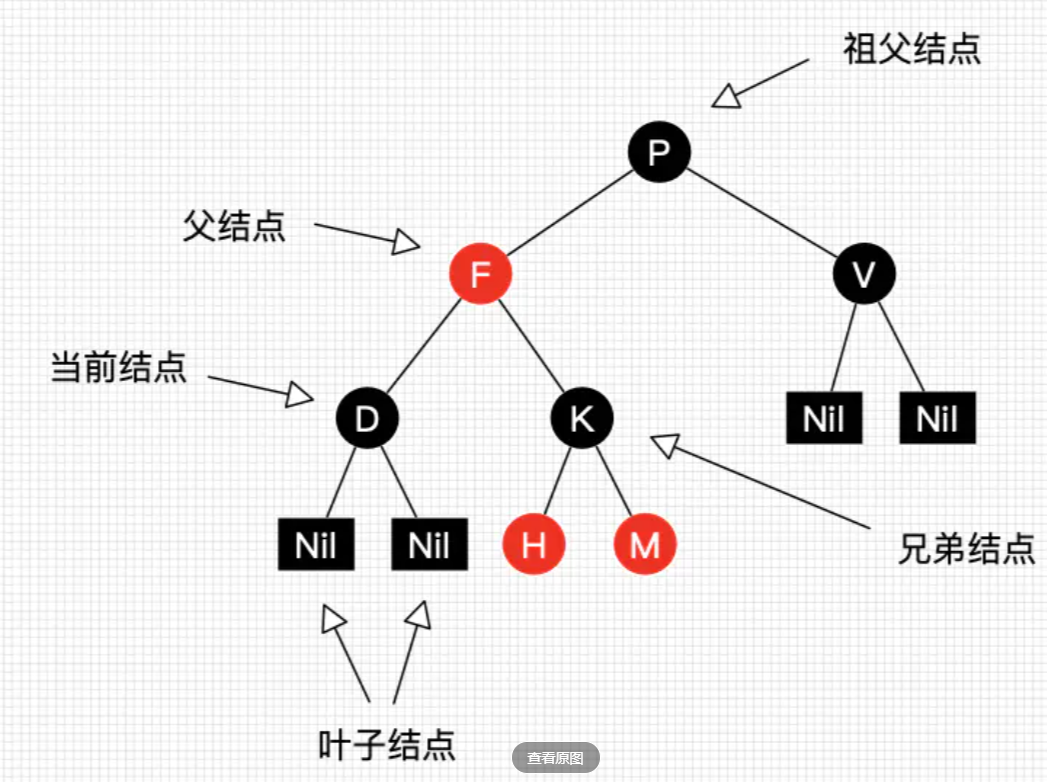
红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质：

• 性质1：每个节点要么是黑色，要么是红色。
• 性质2：根节点是黑色。
• 性质3：每个叶子节点（NIL）是黑色。
• 性质4：每个红色结点的两个子结点一定都是黑色。
• 性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

从性质5又可以推出：

• 性质5.1：如果一个结点存在黑子结点，那么该结点肯定有两个子结点

 

插入

　　1插入结点的父结点为黑结点：

由于插入的结点是红色的，并不会影响红黑树的平衡，直接插入即可，无需做自平衡。

　　2插入结点的父结点为红结点：

　　2.1 父节点和叔叔节点同红色： 父和叔叔变黑，祖父变红

　　2.2 父亲节点（红色）和叔叔节点异色（黑色或者为null）: 选中间值为父节点成为黑色 进行旋转

删除

　　

二叉树删除结点找替代结点有3种情情景：

• 情景1：若删除结点无子结点，直接删除
• 情景2：若删除结点只有一个子结点，用子结点替换删除结点
• 情景3：若删除结点有两个子结点，用后继结点（大于删除结点的最小结点）替换删除结点

删除结点被替代后，在不考虑结点的键值的情况下，对于树来说，可以认为删除的是替代结点！

 

 

 

删除情景1：替换结点是红色结点

　　把替换结点换到了删除结点的位置，把替换结点的颜色设为删除的结点的颜色即可重新平衡

删除情景2：替换结点是黑结点

1兄弟异色（红色），旋转变色（父兄换色）-->兄弟同黑，父节点为红色

 

 

2兄弟同黑色，远侄为红色（近的不用管）---父兄换色  侄子变黑  旋转。

 

 3兄弟同黑色，近侄为红色（远侄黑色）---兄侄交换色 旋转。（换成一条线，红色变中间）（成为了上一种）

 

 

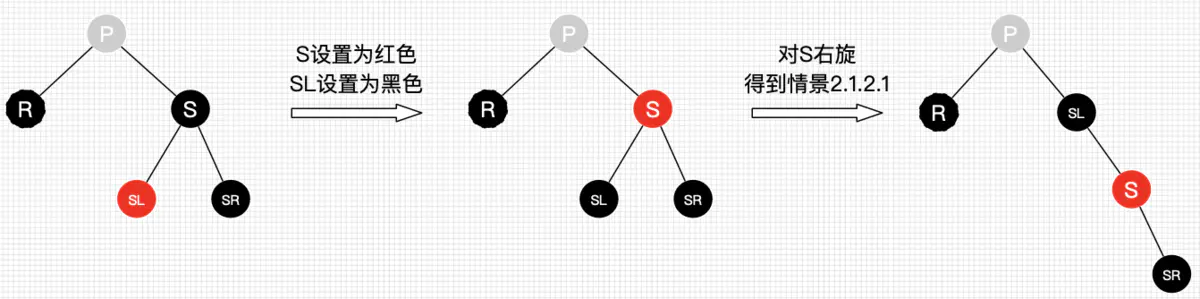
4兄弟侄子都为黑色，--兄弟变色父节点作为新的替补节点