LeetCode题目（按标签）

目录

一、回溯算法

- **回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案**，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

- **回溯法解决的问题都可以抽象为树形结构**：因为回溯法解决的都是在集合中递归查找子集，**集合的大小就构成了树的宽度，递归的深度，都构成的树的深度**。

- 可解决的问题：

  1. 组合问题：N个数里面按一定规则找出k个数的集合
  2. 切割问题：一个字符串按一定规则有几种切割方式
  3. 子集问题：一个N个数的集合里有多少符合条件的子集
  4. 排列问题：N个数按一定规则全排列，有几种排列方式
  5. 棋盘问题：N皇后，解数独等等

- 回溯法模板：

  1. 回溯函数模板返回值以及参数：backtracking，返回值一般为void；先写逻辑，然后需要什么参数，就填什么参数
  2. 回溯函数终止条件：一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归
  3. 回溯搜索的遍历过程：横向+纵向
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

剑指 Offer II 080. 含有 k 个元素的组合

  1. 回溯法
  2. 还有其他解法，不过不重要

剑指 Offer 38. 字符串的排列

  1. 回溯：需要在树枝中记录已经使用的元素
  2. 下一个排列：（未完成）

332重新安排行程（未完成）

  1. 使用Map<String, Map<String, Integer>>记录每个机场可以飞往哪些机场，<出发机场, map<到达机场, 航班次数>>
  2. map中的map需要升序排列

47.全排列II（未完成）

  1. 对树层中前一位去重used[i - 1] == false，对树枝前一位去重用used[i - 1] == true
  2. 对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

46.全排列

  1. 处理排列问题就不用使用startIndex，排列问题，每次都要从头开始搜索
  2. used数组，标记已经选择的元素

491递增子序列(未完成)

  1. 不能使用之前的去重逻辑

  2. used[]：记录本层元素是否重复使用，新的一层uset都会重新定义（清空），所以要知道uset只负责本层

  3. 逻辑： if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) || (used[nums[i] + 100] == 1)) continue;

90子集II（√）

  1. 去重方法：

    • “使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。

    • 要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

    • 树层去重的话，需要对数组排序

    • 可以使用used数组

    • 也可以这样：if (i > startIndex && candidates[i] == candidates[i - 1]) continue;

78子集（√）

  1. 递归参数：start、nums
  2. 终止条件：到达数组顶端
  3. 注意：每次都需要将path中路径添加到结果中

93复原IP地址(未完成)

  1. 递归参数：start（不能重复分割）、pointNum（添加逗号的数量）
  2. 终止条件：分割的段数，点数为3时只需判断第四段是否合法
  3. 遍历到符合条件时，增加点，回溯后删除点

131分割回文串（未完成）

  1. 每次切割一部分，然后在剩下的部分继续切割
  2. 若切割的这部分不是回文串，则拓展该部分，直至该部分为回文串或者结束
  3. 每次将判断是回文串的部分存入path，若分割到了最后，将path存入res

40组合总和II

  1. 去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

39.组合总和

  1. 注意剪枝（sum+nums[i]>target）
  2. 注意可以选取重复元素

17.电话号码的字母组合（未完成）

  1. 注意用map存储数字与元素的对应组合
  2. 每次回溯遍历字符串中一个字符

216组合总和III：和77组合较为相似

77.组合

  1. 回溯函数backtracking（start,n,k）
  2. 终止条件：路径长度==k
  3. 遍历过程：从不同起点遍历
  4. 剪枝条件：起点到终点的长度<k

二、贪心算法

- **贪心的本质是选择每一阶段的局部最优，从而达到全局最优**。
- 贪心的套路：唯一的难点就是如何通过局部最优，推出整体最优。**最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧**。
- 步骤：
  1. 将问题分解为若干个子问题
  2. 找出适合的贪心策略
  3. 求解每一个子问题的最优解
  4. 将局部最优解堆叠成全局最优解

剑指 Offer 14- I. 剪绳子（未完成）

  1. 贪心算法：

942增减字符串匹配（未完成）

  1. 贪心算法：
    • 如果 s[0]=‘I’，那么令 perm[0]=0，则无论 perm[1] 为何值都满足perm[0]<perm[1]；
    • 如果 s[0]=‘D’，那么令 perm[0]=n，则无论 perm[1] 为何值都满足 perm[0]>perm[1]；
    • 问题变为规模为n-1的问题，每次都选择的是最小数和最大数，用两个变量 \textit{lo}lo 和 \textit{hi}hi 表示当前剩余数字中的最小数和最大数。

剑指 Offer II 019. 最多删除一个字符得到回文

  1. 暴力：首先判断原串是否是回文串，如果是，就返回 true；如果不是，则枚举每一个位置作为被删除的位置，再判断剩下的字符串是否是回文串

  2. 贪心算法：

    • 初始化两个指针 low 和 high 分别指向字符串的第一个字符和最后一个字符。每次判断两个指针指向的字符是否相同

    • 如果相同，则更新指针，将 low 加 1，high 减 1，然后判断更新后的指针范围内的子串是否是回文字符串。

    • 如果两个指针指向的字符不同，则两个字符中必须有一个被删除

    • 双指针法判断两种情况下字符是否存在回文串

968监控二叉树（?）

  1. 从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少
  2. 整体最优：全部摄像头数量所用最少
  3. 具体解法：递归判断左右节点的覆盖情况，返回自己的覆盖情况（三种状态：无覆盖、有摄像头、有覆盖）
    • 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头
    • 左右节点至少有一个是无覆盖状态,那 根节点此时应该放一个摄像头

714买卖股票的最佳时机含手续费（?）

  1. 贪心算法：最低值买，最高值（如果算上手续费还盈利）就卖
    • 买入日期：其实很好想，遇到更低点就记录一下。
    • 卖出日期：没有必要算出准确的卖出日期，只要当前价格大于（最低价格+手续费），就可以收获利润，至于准确的卖出日期，就是连续收获利润区间里的最后一天（并不需要计算是具体哪一天）。
  2. 动态规划：略

738单调递增的数字（?）

  1. 局部最优：遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]--，然后strNum[i]给为9，可以保证这两位变成最大单调递增整数。
  2. 全局最优：得到小于等于N的最大单调递增的整数。
  3. 从后向前遍历

56合并区间

  1. 先排序，然后根据重叠区间两端判定是否合并和更新边界

763划分字母区间

  1. 先遍历字符串，找到每个字符出现的最大位置
  2. 再遍历一次，寻找满足条件的片段最多的子串

435无重叠区间

  1. 按照左边界排序，每次更新最小右边界
  2. 若不重叠，则更新为最新元素的右边界；若重叠，则更新为最小的右边界（这里贪心）

452用最少数量的箭引爆气球

  1. 先排序，然后利用边界计算重叠的气球数量
  2. 注意每次最大边界需要更新：若超过，则直接更新，若未超过，则更新为两者最小值

406根据身高重建队列（?）

  1. 使用Arrays.sort排序：身高从大到小排（身高相同k小的站前面）
  2. 使用链表，根据k值插入位置

860柠檬水找零

  1. 计算5块和10块的数量，优先找零10块，每次若5块数量不足，则返回false

135分发糖果

  1. 先比较右边，再比较左边，注意比较左边时，如果已经符合要求，则不用更改
  2. 数组初始化全为1
  3. 采用的思想是两次贪心

134加油站（?）

  1. 每个加油站的剩余量rest[i]为gas[i] - cost[i]，累加一旦小于0，则从下个区间开始。
  2. 若总剩余量小于0，则返回-1

1005K 次取反后最大化的数组和

  1. 局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。
  2. 先翻转负数，如果k还有剩余并且不为偶数，则翻转当前最小值。

45跳跃游戏II（?）

  1. 当前这一步的最大覆盖和下一步最大覆盖。

55跳跃游戏

  1. 跳几步无所谓，关键在于可跳的覆盖范围！
  2. 问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

122买卖股票的最佳时机II(?)

  1. 局部最优：收集每天的正利润
  2. 全局最优：求得最大利润
  3. 动态规划

53最大子数组和(?)

  1. 贪心贪的是哪里：如果 -2 1 在一起，计算起点的时候，一定是从1开始计算，因为负数只会拉低总和
  2. 局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。
  3. 全局最优：选取最大“连续和”
  4. 第二种方法：动态规划

376摆动序列(?)

  1. 局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
  2. 整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。
  3. 贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点。
  4. 做法：记录前一个差值和当前差值
  5. 思路2---动态规划：

445分发饼干

  1. 排序+贪心（小的优先满足小的，大的优先满足大的）

三、动态规划

1. 寻找最优子结构，避免重复计算
2. 问题建模:最优子结构，边界，状态转移公式
3. 求解问题:
   1.备忘录算法
   2.自底向上求解(从简单问题上升到复杂问题)
   3.简单递归
   4.排列组合
4. 步骤：
   - 确定dp数组（dp table）以及下标的含义
   - 确定递推公式
   - dp数组如何初始化
   - 确定遍历顺序
   - 举例推导dp数组
5. 调试：**找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！**

剑指 Offer 46. 把数字翻译成字符串

  1. 递归方程：f(i)=f(i−1)+f(i−2)[i−1≥0,10≤x≤25]

剑指 Offer 60. n个骰子的点数

  1. 递推方程：tmp[j + k] += dp[j] / 6.0;每个点数，影响到下一个数组的六个值，每次需要扩充数组
  2. 初始化：6长度的数组，值都为1/6

剑指 Offer 49. 丑数（未完成）

  1. 最小堆：首先将最小的丑数 1 加入堆。每次取出堆顶元素 x，则 x 是堆中最小的丑数，将 2x, 3x, 5x 加入堆，使用哈希集合去重避免重复元素
  2. 动态规划：

剑指 Offer 47. 礼物的最大价值

  1. 递推公式：dp[ i j ]=Math.max(dp[ i-1 j ],dp[i j-1 ])+grid[ i j ]

剑指 Offer II 101. 分割等和子集（未完成）

剑指 Offer 42. 连续子数组的最大和

  1. 递推公式：dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);

剑指 Offer 10- II. 青蛙跳台阶问题

  1. 递推公式：dp[i]=dp[i-1]+dp[i-2]；下一级台阶跳一下，下两级台阶跳两下

01背包问题（01背包、完全背包、多重背包、分组背包和混合背包）

  1. dp数组以及下标的含义：

    dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

  2. 递推公式：

    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
//取第i个物品或者不取

  3. dp数组如何初始化：

    dp[i][0]=0;
dp[0][j]=j < weight[0]?0:value[0];

  4. 遍历顺序：先遍历物品，然后遍历背包重量

    // weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

  5. 滚动数组：把二维dp降为一维dp，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

    //dp数组的定义：dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]
//递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
//初始化：初始为0
//一维dp数组遍历顺序:倒叙遍历是为了保证物品i只被放入一次！不可以先遍历背包容量嵌套遍历物品
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

完全背包问题

  1. 问题描述：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大

  2. 问题求解：

    //1.遍历顺序：先遍历物品，再遍历背包
//与01背包不同的是：遍历背包时不反序，即代表完全背包的物品是可以添加多次
//在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！
//题目稍稍有点变化，就会体现在遍历顺序上，此时遍历顺序可能不能改变
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

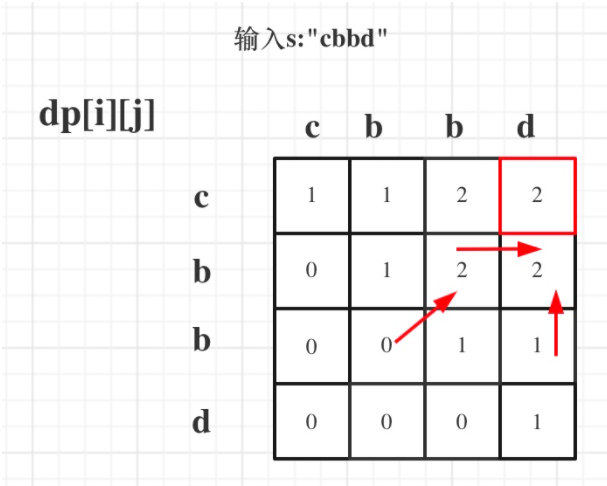
516最长回文子序列

  1. dp含义

    dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

  2. 递推公式：

    if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;
else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

  3. 初始化：

    for (int i = 0; i < s.size(); i++) dp[i][i] = 1;

  4. 遍历顺序： 所以遍历i的时候一定要从下到上遍历，这样才能保证，下一行的数据是经过计算的。

516

647.回文子串（注意遍历顺序？）

  1. 布尔类型的dp[i | j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i | j]为true，否则为false。

  2. 递推公式：

    1.当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。
2.当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况
    -情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
    -情况二：下标i 与 j相差为1，例如aa，也是回文子串
    -情况三：下标i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

  3. 初始化：都初始化为false

  4. 遍历顺序：一定要从下到上，从左到右遍历，这样保证dp[i + 1 | j - 1]都是经过计算的。

  5. 双指针法：中心扩散法（在遍历中心点的时候，要注意中心点有两种情况。一个元素可以作为中心点，两个元素也可以作为中心点。）

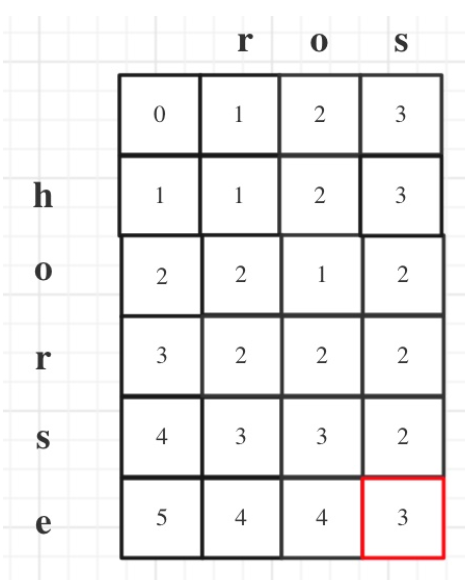
72.编辑距离（?）

  1. dp数组含义：

    dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

  2. 递推公式：

    if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1])，此时就需要编辑了：
    //dp[i][j] = dp[i - 1][j] + 1;
    操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
    //dp[i][j] = dp[i][j - 1] + 1;
    操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
    //word2添加一个元素，相当于word1删除一个元素
    
    //dp[i][j] = dp[i - 1][j - 1] + 1;
    操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。
    
    综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

  3. 初始化：dp[i | 0] = i;同理dp[0 | j] = j;

  4. 遍历顺序：从左到右从上到下去遍历

72

583.两个字符串的删除操作

  1. dp[i | j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。

  2. 递推公式：

    1.当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];
2.当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
    情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
    情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
    情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

  3. 初始化：dp[i | 0] = i；dp[0 | j]=j

  4. 遍历顺序：从上到下，从左到右

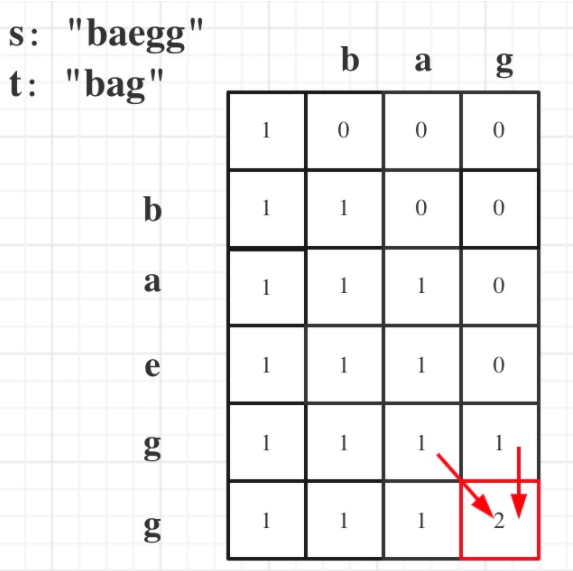
115.不同的子序列（?）

  1. dp[i | j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数。

  2. 递推公式：

    //一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。
当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
//dp[i][j]只有一部分组成，不用s[i - 1]来匹配，即：dp[i - 1][j]
当s[i - 1] 与 t[j - 1]不相等时，dp[i][j] = dp[i - 1][j];

  3. 初始化：dp[i | 0]一定都是1，dp[0 | j]一定都是0

  4. 遍历顺序：从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算

115

392判断子序列

  1. 和1143.最长公共子序列类似
  2. 最后判断结果是否和字符串1的长度相等即可

53最大子序和（?）

  1. dp[i]：包括下标i之前的最大连续子序列和为dp[i]。
  2. 递推公式：dp[i] = max(dp[i - 1] + nums[i], nums[i]);
  3. 初始化：dp[0] = nums[0]
  4. 遍历顺序：递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历
  5. 注意最后的结果可不是dp[nums.size() - 1]！ ，而是最大的result

1035不相交的线

  1. 直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。
  2. 本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

1143.最长公共子序列（?）

  1. dp[ i | j ]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列长度
  2. 递推公式：
    • 如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1|j - 1] + 1;
    • 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大
  3. 初始化：dp[i | 0] = 0;dp[0 | j]也是0
  4. 遍历顺序：从前向后，从上到下来遍历这个矩阵。
  5. 举例推导dp数组

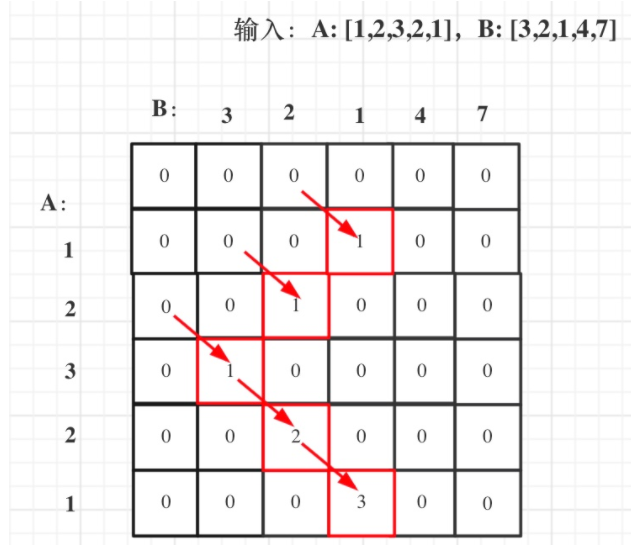
718.最长重复子数组(?)

  1. dp[ i | j ] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度。（若从00开始会比较麻烦）
  2. 递推公式：当A[i - 1] 和B[j - 1]相等的时候，dp[ i j ] = dp[ i - 1 | j - 1] + 1;根据递推公式可以看出，遍历i 和 j 要从1开始
  3. 初始化：dp[i|0] 和dp[0|j]初始化为0
  4. 遍历顺序：外层for循环遍历A，内层for循环遍历B。在遍历的时候顺便把dp[ i | j ]的最大值记录下来。
718

674.最长连续递增序列

  1. dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]。
  2. 递推公式：如果 nums[i + 1] > nums[i]，那么以 i+1 为结尾的数组的连续递增的子序列长度 一定等于 以i为结尾的数组的连续递增的子序列长度 + 1
  3. 初始化：以下标i为结尾的数组的连续递增的子序列长度最少也应该是1，dp[i]应该初始1
  4. 遍历顺序： dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。
  5. 也可以用贪心来做，也就是遇到nums[i + 1] > nums[i]的情况，count就++，否则count为1。记录count的最大值。（若不连续，count从头开始）

300.最长递增子序列

  1. dp含义：dp[i]表示i之前包括i的最长上升子序列的长度。
  2. 状态转移方程：位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
  3. 初始化：每一个i，对应的dp[i]（即最长上升子序列）起始大小至少都是是1
  4. 遍历顺序：dp[i] 是有0到i-1各个位置的最长升序子序列 推导而来，那么遍历i一定是从前向后遍历。
  5. 注意最后的结果不一定是dp[n-1]，应该是dp中的最大值

309最佳买卖股票时机含冷冻期（?）

  1. 四种状态：

    • 状态一：买入股票状态（今天买入股票，或者是之前就买入了股票然后没有操作）
    • 卖出股票状态，这里就有两种卖出股票状态
      • 状态二：两天前就卖出了股票，度过了冷冻期，一直没操作，今天保持卖出股票状态
      • 状态三：今天卖出了股票
    • 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

  2. 递推公式：

    dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];

188.买卖股票的最佳时机IV

  1. 和买卖股票的最佳时机III类似，改成多次买卖，然后用循环计算即可

123买卖股票的最佳时机III(?)

  1. dp数组以及下标的含义：dp[ i ] [ j ]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。

    a.一天一共就有五个状态:0.没有操作 1.第一次买入 2.第一次卖出 3.第二次买入 4.第二次卖出
b.dp[i][1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票

  2. 递推公式：

    dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]); 
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

  3. 初始化：

    dp[0][0] = 0;dp[0][1] = -prices[0];dp[0][2] = 0;dp[0][3] = -prices[0];dp[0][4] = 0;
//第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次

  4. 遍历顺序：一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

122买卖股票的最佳时机II(?)

  1. 和买卖股票的最佳时机的递推公式不同：

            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。
        dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);

121买卖股票的最佳时机(?)

  1. 暴力、贪心（取最左最小值，取最右最大值，那么得到的差值就是最大利润）

  2. 动态规划：（有点没懂）

    1.dp数组：dp[i][0] 表示第i天持有股票所得最多现金；dp[i][1] 表示第i天不持有股票所得最多现金
2.递推公式：
    dp[i][0] = max(dp[i - 1][0], -prices[i]);//选较小的买入
    dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
3.初始化：dp[0][0] -= prices[0];dp[0][1] = 0;
4.从前向后遍历

337.打家劫舍III(?)

  1. 对于树的话，首先就要想到遍历方式，前中后序（深度优先搜索）还是层序遍历（广度优先搜索）

  2. 本题一定是要后序遍历，因为通过递归函数的返回值来做下一步计算。关键是要讨论当前节点抢还是不抢。

  3. 暴力递归、记忆化递推（使用一个map把计算过的结果保存一下）

  4. 动态规划

    • 确定递归函数的参数和返回值：偷与不偷的两个状态所得到的金钱，那么返回值就是一个长度为2的数组（dp数组）
    • 终止条件：空节点的话，很明显，无论偷还是不偷都是0（相当于dp数组的初始化）
    • 遍历顺序：使用后序遍历。 因为通过递归函数的返回值来做下一步计算。
    • 单层递归的逻辑：
      1. 偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0];
      2. 不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1]);
      3. 最后当前节点的状态就是{val2, val1}; 即：

213打家劫舍II（?）

  1. 三种情况：其中情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了
    • 考虑不包含首尾元素
    • 考虑包含首元素，不包含尾元素
    • 考虑包含尾元素，不包含首元素
  2. 对于每种情况就简化为打家劫舍的基本情况，求最大值

198打家劫舍

  1. dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
  2. dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
  3. 初始化：dp[0] = nums[0]; dp[1] = max(nums[0], nums[1]);
  4. 循环：for (int i = 2; i < nums.size(); i++) dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

139单词拆分（?）

  1. dp含义：dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。
  2. 递推公式： if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
  3. 初始化：dp[0]=true，下标非0的dp[i]初始化为false

279完全平方数：完全背包问题，类似322.零钱兑换

322零钱兑换

  1. dp[j]：凑足总额为j所需钱币的最少个数为dp[j]
  2. dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
  3. 初始化：dp[0]=0,dp[i]=Integer.MAX_VALUE；（考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。所以下标非0的元素都是应该是最大值。）
  4. 要求最少硬币数量，硬币是组合数还是排列数都无所谓！所以两个for循环先后顺序怎样都可以！

377组合总和IV：完全背包问题求排列（？）

  1. 遍历顺序：内层for循环遍历物品，外层for遍历背包（计算排列数）

518零钱兑换II（?）

  1. dp[j]：凑成总金额j的货币组合数为dp[j]
  2. 递推公式：dp[j] += dp[j - coins[i]];
  3. 初始化：dp[0] = 1
  4. 遍历顺序：（有待理解）
    • 外层for循环遍历物品（钱币），内层for遍历背包（金钱总额）：dp[j]里计算的是组合数
    • 内层for循环遍历物品（钱币），外层for遍历背包（金钱总额）：dp[j]里计算的是排列数
  5. 本题和纯完全背包不一样，纯完全背包是能否凑成总金额，而本题是要求凑成总金额的个数！
  6. 求装满背包有几种方法，一般公式都是：dp[j] += dp[j - nums[i]];

4740和1

  1. 也是01背包问题，m和n是书包的两个属性，每个字符视作一个物品，字符的0和1 的数量对应物品大小，每个字符价值视作1

  2. dp含义：初始化为1即可

    dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

  3. 递推公式：每次需要统计当前物品的0和1的数量

    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

494.目标和(?)

  1. 转化为01背包问题：加法的总和为x，那么减法对应的总和就是sum - x，由题意x - (sum - x) = S，则x = (S + sum) / 2——问题就转化为，装满容量为x背包，有几种方法。

  2. (S + sum) / 2 计算的过程中向下取整有影响

    if ((S + sum) % 2 == 1) return 0; // 此时没有方案
if (abs(S) > sum) return 0; // 此时没有方案

  3. dp含义：dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

  4. 递推公式：dp[j] += dp[j - nums[i]]，（所以求组合类问题的公式，都是类似这种）

  5. dp初始化：dp[0]=1（装满容量为0的背包，有1种方法，就是装0件物品）

  6. 求组合类问题的公式，都是类似这种：dp[j] += dp[j - nums[i]]

1049.最后一块石头的重量II

  1. 尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了

416分割等和子集(?)

  1. 集合里能否出现总和为 sum / 2 的子集
  2. 转换为01背包问题

96不同的二叉搜索树(?)

  1. dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
  2. 递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量(j为头结点，取值范围为1<=j<=i)
  3. dp[0]：代表空节点，只有一种

343.整数拆分(?)

  1. dp[i] 为正整数 i 拆分后的结果的最大乘积

  2. 递推公式

    dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
//j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了。
//每次计算dp[i]，取最大,所以需要max中加上dp[i]

  3. dp[0] dp[1] 不应该初始化，也就是没有意义的数值，只初始化dp[2] = 1

63.不同路径II（存在障碍物）(?)

  1. 有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）

    dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

  2. dp数组如何初始化

    for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
//一旦遇到障碍，后续都到不了

62.不同路径

  1. 递推公式：

    dp[i][j]=dp[i][j-1]+dp[i-1][j];//边界为1

  2. 初始化：

    for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

746最小花费爬楼梯

  1. dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]
  2. dp[i]的定义：到达第i个台阶所花费的最少体力为dp[i]
  3. 注意这里为什么是加cost[i]，而不是cost[i-1],cost[i-2]之类的，因为题目中说了：每当你爬上一个阶梯你都要花费对应的体力值
  4. 注意最后一步可以理解为不用花费，所以取倒数第一步，第二步的最少值
  5. 可不使用dp，只维护两个数

70爬楼梯

  1. dp[i] = dp[i - 1] + dp[i - 2]
  2. 可以使用完全背包问题求排列的方法

509斐波那契数

  1. 递归
  2. 维护两个数值

5最长回文子串(?)

  1. 对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。

  • 子串长度大于2：P(i,j)=P(i+1,j−1)∧(Si​==Sj​)

  • 子串长度为1或2：P(i,i)=true、P(i,i+1)=(Si​==Si+1​)​

  • 在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

  1. 中心扩展算法

    对边界情况进行枚举，边界情况即为回文中心
    枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度

22括号生成

  1. 回溯法：参数是左右括号个数和最大括号个数，字符串长度达到最大时加入结果集，左括号小于最大时加左括号，右括号小于左括号时，可以加入右括号。

45跳跃游戏 II

  1. 贪心算法：从后往前找，每次找到能够到达该位置并且距离该位置最远的点，步数加一
  2. 贪心算法：正向遍历，每次寻找最大边界，每次到达边界时步数加一
  3. 动态规划：dp[i] 代表到位置i的最少步数，每次遍历i之前的元素得到dp[i]的值

64最小路径和

  1. 动态规划：dp(i,j) 代表到这个点的最小距离，每个位置可以从其上左两个位置的最小值得到，需要初始化边界

91解码方法

  1. 动态规划： 每次判断当前元素是否为0，以及当前元素和前一个元素组合是否在范围内，满足一个条件则加上对应方法数。

95不同的二叉搜索树 II（?）

  1. 回溯法：定义 generateTrees(start, end) 函数表示当前值的集合为 返回序列生成的所有可行的二叉搜索树。先生成左右子树，然后遍历左右子树，每次从中选取左右子树拼接为一棵树

四、数据库

181.超过经理收入的员工

  1. 使用where
  2. join

196.删除重复的电子邮箱

  1. 使用delete和where；将表本身和自己关联起来

五、二叉树

剑指 Offer 07. 重建二叉树（未完成）

  1. 同105.从前序与中序遍历序列构造二叉树

538.把二叉搜索树转换为累加树(?)

  1. 递归：设置一个全局变量
  2. Morris 遍历：（未看）

108.将有序数组转换为二叉搜索树

  1. 递归

669.修剪二叉搜索树

  1. 递归：判断大小关系进行递归
  2. 迭代：设置两个指针分别判断左子树、右子树和low、high的大小关系，不断剪去不符合条件的子树，要注意左子树的右孩子和右子树的左孩子可能符合条件。

450.删除二叉搜索树中的节点

  1. 先定位，再将子树调整，使用左子树最大值或者右子树最小值代替需要删除的节点，再调整删除节点的子树
  2. 迭代：只需将递归改为迭代即可

701.二叉搜索树中的插入操作

  1. 递归

  2. 按搜索方法遍历，找到位置后插入

236二叉树的最近公共祖先(未完成)

  1. 递归：最近公共祖先的情况无外乎三种情况，解答此题最好分别画出三种情况的草图，问题便迎刃而解
  • 树形一：root为p,q中的一个，这时公共祖先为root
    • 树形二：p,q分别在root的左右子树上（p在左子树，q在右子树；还是p在右子树，q在左子树的情况都统一放在一起考虑）这时满足p,q的最近公共祖先的结点也只有root本身
    • 树形三：p和q同时在root的左子树；或者p,q同时在root的右子树，这时确定最近公共祖先需要遍历子树来进行递归求解。

  1. 存储父节点：

    • 可用后序遍历，栈中存储的就是祖先节点，将其中一个遍历的结果放入Set中，然后一次判断另一个结果最先与set中匹配的值
    • 遍历根节点时用哈希集合记录遍历过的值
    • 遍历p节点时，用哈希表记录父节点路径
    • 遍历q节点时，查看哈希记录里面有无同样的值

501.二叉搜索树中的众数（还没看）(?)

530.二叉搜索树的最小绝对差

  1. 中序遍历：有序，只需要比较相邻

98.验证二叉搜索树

  1. 递归：

    //lower和upper为上下界
//遍历左子树设置上界，遍历右子树设置下界
public boolean isValidBST(TreeNode node, long lower, long upper)

  2. 中序遍历：当前的值是否大于上一个值

700.二叉搜索树中的搜索

  1. 递归Or层次遍历

617.合并二叉树

  1. 递归
  2. 迭代：层次遍历，三个队列，依次判断每次遍历的原始树的左右子树

654.最大二叉树(?)

  1. 递归

  2. 单调栈解法：

以测试案例为例，一个输入序列：[3, 2, 1, 6, 0, 5]。 设置一个辅助栈，从大到小存储。 过程如下：

  • 首先入栈3
  • 2 比 3 小，入栈
  • 1 比 2 小，入栈
  • 6 大于1，因此要弹出1，1在2和6之间选择二者之间较小的元素作为父节点，因此选择2。1在2的右侧，使得1作为2的右子节点
  • 弹出1后，6仍然比2大，同理2要在3和6之间选择一个作为父节点。3比6小，因此选择3。2在3的右侧，因此2作为3的右子节点
  • 同理弹出3，让3作为6的左子节点
  • 入栈6
  • 入栈0
  • 入栈5的时候比0大，要弹出0，选择5作为父节点，并且0是5的左孩子
  • 弹出5，左侧是6，作为5的父节点
  • 6最后弹出，就是根节点
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        Stack<TreeNode> stack=new Stack<>();
        TreeNode p=null;
        for(int i=0;i<nums.length;i++){
            p=new TreeNode(nums[i]);
            while(!stack.empty()&&stack.peek().val<p.val){
                TreeNode t=stack.pop();
                if(!stack.empty()&&p.val>stack.peek().val){stack.peek().right=t;
                else p.left=t;
            }
            stack.push(p);
        }

        while(!stack.empty()){
            p=stack.pop();
            if(!stack.empty())stack.peek().right=p;
        }

        return p;
    }
}

105.从前序与中序遍历序列构造二叉树(?)

  1. 递归：和106类似

  2. 迭代：（未理解）

    • 对于前序遍历中的任意两个连续节点 u 和 v，根据前序遍历的流程，我们可以知道 u 和 v 只有两种可能的关系：

    • v 是 u 的左儿子。这是因为在遍历到 u 之后，下一个遍历的节点就是 u 的左儿子，即 v；

    • u 没有左儿子，并且 v 是 u 的某个祖先节点（或者 u 本身）的右儿子。如果 u 没有左儿子，那么下一个遍历的节点就是 u 的右儿子。如果 u 没有右儿子，我们就会向上回溯，直到遇到第一个有右儿子（且 u 不在它的右儿子的子树中）的节点 u_a，那么 v 就是 u_a的右儿子。

106.从中序与后序遍历序列构造二叉树(?)

  1. 递归：定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界，递归入口为helper(0, n - 1) ：（O(n)、O(n)）

    • 如果 in_left > in_right，说明子树为空，返回空节点。
    • 选择后序遍历的最后一个节点作为根节点。
    • 利用哈希表 O(1)O(1) 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树，从 index + 1 到 in_right 属于右子树。
    • 根据后序遍历逻辑，递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)。注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。
    • 返回根节点 root。

  2. 迭代（未理解）

112路径总和

  1. 递归
  2. 广度优先搜索：使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和

513.找树左下角的值

  1. 层次遍历：记录高度

404.左叶子之和

  1. 递归
  2. 迭代：层次遍历（广度优先）

257二叉树的所有路径（未完成）

  1. 递归（深度优先）
  2. 广度优先：
    • 节点队列、路径队列
    • 在每一步迭代中，我们取出队列中的首节点，如果它是叶子节点，则将它对应的路径加入到答案中。如果它不是叶子节点，则将它的所有孩子节点加入到队列的末尾

222完全二叉树的节点个数（未完成）

  1. 二分查找 + 位运算：

    • 对于最大层数为 hh 的完全二叉树，节点个数一定在 [2h,2h+1−1] 的范围内
    • 根据节点个数范围的上下界得到当前需要判断的节点个数 k，如果第 kk个节点存在，则节点个数一定大于或等于 kk，如果第 k 个节点不存在，则节点个数一定小于 k，由此可以将查找的范围缩小一半，直到得到节点个数。
    • 判断第 k 个节点是否存在呢？如果第 k 个节点位于第 h 层，则 k 的二进制表示包含 h+1位，其中最高位是 1，其余各位从高到低表示从根节点到第 k 个节点的路径，0 表示移动到左子节点，1 表示移动到右子节点。通过位运算得到第 k 个节点对应的路径，判断该路径对应的节点是否存在，即可判断第 k 个节点是否存在。
    • 时间复杂度：O(log2n)；空间复杂度：O(1)

  2. 递归

  3. 迭代：层次遍历

559N 叉树的最大深度

  1. 递归
  2. 层次遍历：记录每次每层最后一个节点

104二叉树的最大深度

  1. 递归：深度优先
  2. 迭代：层次遍历

101对称二叉树

  1. 镜像条件---两个树互为镜像：它们的两个根结点具有相同的值；每个树的右子树都与另一个树的左子树镜像对称
  2. 递归：函数----检测两个树是否是镜像
  3. 迭代：使用队列，每次入队需要判定是否是镜像的子树

226.翻转二叉树

  1. 递归
  2. 迭代（未解决）

111二叉树的最小深度

  1. 层次遍历：广度优先
  2. 递归：深度遍历

117填充每个节点的下一个右侧节点指针II

  1. 层次遍历：还是使用栈
  2. 利用已知的next指针：上层建立下层的next指针，用last（上一个节点）和nextStart（下一层的开始节点）进行记录

116填充每个节点的下一个右侧节点指针

  1. 层次遍历
  2. 使用已有的next指针，利用父节点完成子节点的连接

515在每个树行中找最大值

  1. 层次遍历：每次求最大值

429N叉树的前序遍历

  1. 层次遍历（广度优先）
  2. 递归：每次遍历一层

637二叉树的层平均值

  1. 层次遍历（广度优先）
  2. 深度遍历（未看）

199二叉树的右视图

  1. 层次遍历：只是每次只记录每层最后一个节点
  2. 深度优先/广度优先（代码未看）

144二叉树前序遍历、94二叉树中序遍历、145二叉树后序遍历

  1. 递归
  2. 迭代（栈）
  3. Morris遍历（未理解）

102.二叉树的层序遍历

  1. 队列：使用指向每层最后一个的指针；或者记录当前层大小的数据（即当前队列大小）

107二叉树的层序遍历II（自底向上遍历）

  1. 和自顶向下遍历类似；使用list.add（0，level），从前面开始添加每一层即可。

六、栈与队列

剑指 Offer 31. 栈的压入、弹出序列（未完成）

  1. 利用栈进行模拟：模拟进栈与出栈
    • 入栈操作： 按照压栈序列的顺序执行。
    • 出栈操作： 每次入栈后，循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立，将符合弹出序列顺序的栈顶元素全部弹出。
    • 最后查看栈是否为空

385迷你语法分析器（看不懂）

347前K个高频元素（未完成）

  1. 堆：先用HashMap记录次数，然后建立堆，逐次判断每个元素是否被插入。然后维持一个k大小的堆，最后输出该堆

  2. 快速排序：基于快速排序的方法，求出「出现次数数组」的前 kk 大的值。每次分割为两部分，判断前一部分与k的大小。

239滑动窗口最大值（未完成）

  1. 优先队列（堆）：先加入k个数据，然后每次新加入元素，并判断加入后当前最大元素是否已经滑出窗口。将当前最大加入结果数组。
  2. 单调队列
  3. 分块+预处理

150逆波兰表达式求值

  1. 就是后缀表达式求值，用栈，不过要注意类型转换
  2. 可以用数组模拟栈，用top指针

1047删除字符串中的所有相邻重复项

  1. 类似于括号匹配，使用栈

20有效的括号

  1. 使用栈，发现有括号，一旦不匹配或者栈为空，则返回false

232用栈实现队列

  1. 两个栈，一个进入，一个出

225用队列实现栈（未完成）

  1. 两个队列：每次push，先放入q2，然后将q1的元素放入q2，然后交换q1和q2
  2. 一个队列：每次push，先放入元素，然后将其之前的元素先出队然后再入队

七、字符串

剑指 Offer II 032. 有效的变位词（未完成）

  1. 先判断源字符串是否相等，然后排序，判断排序后字符串是否相等
  2. 26长度的数组记录第一个字符串中单词数量，然后遍历第二个字符串

824山羊拉丁文

  1. 遍历+判断+拼接

388文件的最长绝对路径（未完成）

  1. 栈
  2. 遍历

43字符串相乘（未完成）

  1. 做加法：
  2. 做乘法：

821字符的最短距离

  1. 两次遍历：

    • 问题可以转换成，对 s 的每个下标 i，求s[i] 到其左侧最近的字符 c 的距离，s[i] 到其右侧最近的字符 c 的距离

    • 对于前者，我们可以从左往右遍历 s，若 s[i]=c则记录下此时字符 c 的的下标 idx。遍历的同时更新answer[i]=i−idx。

    • 对于后者，我们可以从右往左遍历s，若 s[i]=c 则记录下此时字符 c 的的下标 idx。遍历的同时更新 answer[i]=min(answer[i],idx−i)。

    • 代码实现时，在开始遍历的时候 idx 可能不存在，为了简化逻辑，我们可以用 −n 或 2n 表示，这里 n 是 s 的长度。（之后会被替换）

剑指 Offer 20. 表示数值的字符串（未完成）

  1. 自动机

8字符串转换整数 (atoi)（未完成）

  1. 自动机：从一个状态遇到另一个状态会发生什么操作

796.旋转字符串

  1. 若是源字符串可以旋转得到目标字符串，则两个源字符串拼接起来一定包含目标字符串。

459.重复的子字符串（未完成）

  1. 枚举：

    n 一定是 n ′的倍数；

    s ′ 一定是 s 的前缀；

    对于任意的 ii∈[n ′ ,n)，有 s[i] =s[i−n ′ ]。

  2. 字符串匹配：我们将两个 ss 连在一起，并移除第一个和最后一个字符。如果 s 是该字符串的子串，那么 s 就满足题目要求。

  3. KMP算法：

28.实现strStr()（未完成）

  1. 暴力遍历：设置标志位，每次改变初始位置开始遍历

  2. 常见的字符串匹配算法包括暴力匹配、Knuth-Morris-Pratt 算法、Boyer-Moore 算法、Sunday 算法等，本文将讲解 Knuth-Morris-Pratt 算法。

    • Knuth-Morris-Pratt 算法（KMP）

58.左旋转字符串

  1. substring拼接：切片+拼接
  2. 遍历：遍历字符串，分两段遍历，拼接即可，可采用取模操作简化代码

151.翻转字符串里的单词（未完成）

  1. 字符串特性（利用自带方法）
  2. 不使用java内置方法：

5.替换空格

  1. 将字符串转换为数组

541.反转字符串II

  1. 将字符转换为数组，然后逆转
  2. 翻转的时候取（i+k，n）的最小值，实际值翻转k，只是每次增加2k的步长

八、哈希表

398随机数索引（未完成）

  1. 哈希表：key=target，value是target对于的下标列表，遍历数组
  2. 水塘抽样：遍历 nums，当我们第 i 次遇到值为 target 的元素时，随机选择区间 [0,i) 内的一个整数，如果其等于 0，则将返回值置为该元素的下标，否则返回值不变。

819最常见的单词

  1. 哈希表+计数：麻烦一点的是处理的过程，注意最后一个单词的统计（ 可使用i <= length）

380O(1) 时间插入、删除和获取随机元素（未完成）

  1. 变长数组 + 哈希表：数组记录元素，哈希表记录元素及其在List中的位置；移除则是将List中最后一位补到Map中获取到的位置。

1502判断能否形成等差数列

  1. 先排序，然后遍历
  2. 首先遍历一遍数组找到最大值和最小值，同时将每个数放到一个hashSet中， 计算公差d=（最大值-最小值）/（数组元素个数-1）， 再从最小值开始，每次增加一个公差d，判断hashSet中是否存在，如果不存在则不是等差序列， 如果一直到最后都存在， 则是等差。

804唯一摩尔斯密码词

  1. 使用暴力模拟+哈希表的方法遍历即可

18.四数之和

  1. 在三数之和上再加一层循环

15.三数之和

  1. 双指针法：先排序，然后固定一个指针，其他left和right指针遍历，注意当前sum和target作比较来剪枝

1.两数之和

  1. 哈希表：遍历数组，并查看哈希表中是否有target-num[i]，若无则把当前元素也加入哈希表。

383.赎金信

  1. hashmap
  2. int[26]:感觉两个字符匹配的都可以中数组

454.四数相加II

  1. 前两个数组相加存入HashMap，判断后两个数组相加元素是否与Map中元素相加为0

202.快乐数

  1. 两种可能情况：到1或者进入循环，于是用HashSet判断，如果有重复，则不是快乐数。
  2. 快慢指针：相当于判断链表是否有环，每次生成两个未来的数

349.两个数组的交集

  1. HashSet
  2. 排序+双指针，注意要保存前一个交集中的元素指针，防止重复

242有效的字母异位词

  1. 先排序，后equal
  2. 哈希表
  3. char[26]

九、树

1305两棵二叉搜索树中的所有元素（未完成）

  1. 中序遍历 + 归并：

剑指 Offer 54. 二叉搜索树的第k大节点（未完成）

  1. 中序遍历倒序：先遍历右子树，然后遍历根节点，再遍历左子树，每遍历一个节点K减一，K=0时找到值

429.N 叉树的层序遍历

  1. 采用层序遍历：队列

310.最小高度树（?）

104.二叉树的最大深度

  1. 递归（和深度优先搜索类似）
  2. 广度优先搜索

110.平衡二叉树

  1. 求深度，比较绝对值
  2. 可在求深度过程中判断是否子树是平衡二叉树，如不是，返回-1，避免父节点做多余处理

十、链表

剑指 Offer II 077. 链表排序（未完成）

  1. 排序：用List记录值，然后排序，再写回链表
  2. 自顶向下归并排序
  3. 自底向上归并排序

141环形链表

  1. 同142环形指针

剑指 Offer II 027. 回文链表（未完成）

  1. 将值复制到数组中后用双指针法
  2. 递归：
  3. 快慢指针：找到前半部分链表的尾节点，反转后半部分链表，判断是否回文，恢复链表，返回结果。

剑指 Offer II 024. 反转链表

  1. 同206反转链表

剑指 Offer 52. 两个链表的第一个公共节点

  1. 7链表相交

剑指 Offer 18. 删除链表的节点

  1. 分两步：定位节点、修改引用。

707设计链表（未完成）

  1. 节点类、空头结点、链表大小size

203移除链表元素

  1. 递归or迭代

86分隔链表

  1. 设置两个字链表，分别保存相应链表，最后连接

81删除排序链表中的重复元素

  1. 较为简单，一次遍历，判断，若相等便跳过删除

82删除排序链表中重复出现过的元素

  1. 设置重复值，设置头结点，若出现重复情况，则根据重复值判定删除，删除完毕后，移到下一个节点

61旋转链表：将链表每个节点向右移动 k个位置

  1. 闭合为环：新链表的最后一个节点为原链表的第 (n - 1) - (k mod n)(n−1)−(k mod n) 个节点（从 0 开始计数）
  2. 找到倒数第k个节点，pre+tali

25.k个一组翻转链表

  1. 方法：
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode hair = new ListNode(0);
        hair.next = head;
        ListNode pre = hair;
        
        while (head != null) {
        ListNode tail = pre;
        // 查看剩余部分长度是否大于等于 k
        for (int i = 0; i < k; ++i) {
            tail = tail.next;
            if (tail == null) {
                return hair.next;
            }
        }
        ListNode nex = tail.next;
        ListNode[] reverse = myReverse(head, tail);
        head = reverse[0];
        tail = reverse[1];
        // 把子链表重新接回原链表
        pre.next = head;
        tail.next = nex;
        pre = tail;
        head = tail.next;
        }
        return hair.next;
    }
    public ListNode[] myReverse(ListNode head, ListNode tail) {
        ListNode prev = tail.next;
        ListNode p = head;
        while (prev != tail) {
            ListNode nex = p.next;
            p.next = prev;
            prev = p;
            p = nex;
        }
        return new ListNode[]{tail, head};
    }
}

23合并k个升序列表

  1. 暴力解法：每次合并lists[0]和下一个元素
  2. 归并：（注意递归和迭代两种表示方法）
  3. 优先队列合并：维护当前每个链表没有被合并的元素的最前面一个，k 个链表就最多有 k 个满足这样条件的元素，每次在这些元素里面选取 val 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以用优先队列来优化这个过程。

21合并两个有序链表

  1. 交错判读
  2. 递归:每次比较两个节点，将较小者加入结果，其余递归合并。
  3. 迭代:就是交错

142环形指针II

  1. 哈希表记录已经遍历过的指针，再次遇到便是环入口
  2. 快慢指针：a+(n+1)b+nc=2(a+b)------快指针走过慢指针两倍：O(n)、O(1)
    • 设 环的长度为A,慢指针在入环的时候快指针在环中的位置B(取值范围0到A-1),当快慢指针相遇时 [慢指针在环中走了C] ,有C % A = ( B + 2C) % A,等价于
      An + C = B + 2C,合并得C = An - B，当 n=1 时 , 0 <= C < A，故 慢指针在第一圈必定能和快指针相遇
    • 从相遇点到入环点的距离加上 n-1n−1 圈的环长，恰好等于从链表头部到入环点的距离。
    • 当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

7链表相交

  1. 暴力遍历
  2. 计算长度差值，移到相同位置，开始遍历，只需要两次遍历
  3. 一直遍历，走得快的一定会追上走得慢的
  4. 使用哈希集合，将链表A放入集合，然后遍历链表B
  5. 双指针法：使用两个指针指向两个链表，判断是否相等，若遍历到末尾则指向另一条链表，可以证明方法可行

19删除链表的倒数第n个节点

  1. 暴力解法：先遍历一遍统计个数，然后找到倒数第n个(length-n+1)。

  2. 使用栈

  3. 双指针，指针相差n个位置。可先设置空头结点，最后返回空头结点的下一个位置。

    P.S.链表操作都可设置一个哑结点(类似空头结点)，简化操作。

24两两交换链表中的节点

  1. 递归：先交换后续链表，然后只需要对最前面两个节点进行交换；原始链表的头节点变成新的链表的第二个节点，原始链表的第二个节点变成新的链表的头节点。

    class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = head.next;
        head.next = swapPairs(newHead.next);
        newHead.next = head;
        return newHead;
    }
}

  2. 迭代：采用虚拟头结点进行迭代

707设计链表

206反转链表

十一、数组

剑指 Offer 56 - II. 数组中数字出现的次数 II（未完成）

  1. 暴力破解
  2. 有限状态自动机
  3. 遍历统计

442数组中重复的数据（未完成）

  1. 先排序，然后遍历
  2. 将元素交换到对应的位置：利用nums[i]-1=i的规则,先遍历一次交换，然后遍历一次得到结果
  3. 使用正负号作为标记

剑指 Offer 45. 把数组排成最小的数（未完成）

  1. 排序：自定义排序、内置排序函数，将整数数组转化为字符串数组，然后进行排序，然后拼接起来，注意排序规则

713乘积小于 K 的子数组（未完成）

  1. 二分查找：比较麻烦（未完成）
  2. 连续子数组——滑动窗口：寻找以每个 right 指针为右边界的有效连续子树组的个数（right - left+1），所以不会重复计数

905按奇偶排序数组

  1. 双指针：一次遍历，交换

剑指 Offer 61. 扑克牌中的顺子（未完成）

  1. 此 5 张牌是顺子的 充分条件 如下：

    • 除大小王外，所有牌无重复 ；
    • 设此 5 张牌中最大的牌为 max ，最小的牌为 min （大小王除外），则需满足：max−min<5

  2. 集合 Set + 遍历

  3. 排序 + 遍历

396旋转函数（未完成）

  1. 迭代：当 1≤k<n 时，F(k)=F(k−1)+numSum−n×nums[n−k]

剑指 Offer 39. 数组中出现次数超过一半的数字

  1. 哈希表：存储每个数的个数
  2. Boyer-Moore 投票算法：定义一个计数器，遍历到不同的数减一，相同的数加一
  3. 排序：数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为⌊ n/2 ⌋ 的元素（下标从 0 开始）一定是众数。
  4. 随机化：由于一个给定的下标对应的数字很有可能是众数，我们随机挑选一个下标，检查它是否是众数，如果是就返回，否则继续随机挑选。判断是否大于数组长度一半。
  5. 分治：

剑指 Offer 40. 最小的k个数（未完成）

  1. 普通排序：先排序，然后输出前k个数
  2. 堆排序：
    • 大根堆实时维护数组的前 k小值，使用PriorityQueue，重写compare函数
    • 将前 k 个数插入大根堆中，随后从第 k+1个数开始遍历，如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到的数
    • 最后将大根堆里的数存入数组返回
  3. 快排思想：

剑指 Offer 17. 打印从1到最大的n位数

  1. 计算最大值，然后将数值依次输入数组

  2. 考虑大数问题：递归

    • 表示大数的变量类型：大数的表示应用字符串 String 类型。

    • 生成数字的字符串集：生成的列表实际上是 n 位 0 - 9 的 全排列 ，因此可避开进位操作，通过递归生成数字的 String 列表。

    • 递归生成全排列：基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 n = 2 时（数字范围 1−99 ），固定十位为 0 - 9 ，按顺序依次开启递归，固定个位 0 - 9 ，终止递归并添加数字字符串。

剑指 Offer 29. 顺时针打印矩阵（未完成）

  1. 模拟：int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};每次mod4取出下一个方向
  2. 按层模拟：int left = 0, right = columns - 1, top = 0, bottom = rows - 1;遍历一圈然后往内层遍历

6Z 字形变换（未完成）

  1. 主要是考虑计算二维数组的长度以及何时进行移动

575分糖果

  1. 贪心：取set和n/2的最小值

5螺旋数组（?）

  1. 模拟：主要问题(改变方向)---O(n^2)、O(1)

    int[][] derections={{0,1},{1,0},{0,-1},{-1,0}};

  2. 按层模拟：每个环算作一层，依次遍历四条边：left、right、top、bottom

209长度最小的子数组（?）

  1. 暴力循环：O(n^2)、O(1)

  2. 滑动窗口：定义两个指针 start}和end 分别表示子数组（滑动窗口）的开始位置和结束位置，维护变量sum 存储子数组中的元素和【O(n)、O(1)】

977有序数组的平方

  1. 先平方，再排序
  2. 找到中间边界，再每次比较
  3. 从两边依次找到最大

704二分查找

33搜索旋转排序数组

  1. 二分查找：先分为两部分，判断哪部分有序，再判断target是否在该部分中，否则继续二分查找另一部分，注意判断有序时，直接判断0-mid，该部分无序，则另一部分一定有序。时间复杂度logn

31下一个排列

  1. 先从后往前找反序对，此时后面必定是降序，从降序中找到最小的大于i的数，然后交换，此时i+1后还是降序，使用双指针交换变为升序

27移除元素

  1. 双指针：优化，指针分别指向两端，双向移动，右指针覆盖左指针，重合遍历完

26删除有序数组中的重复项

  1. 双指针

18四数之和

  1. 先排序，然后四重循环
  2. 注意判断重复元素
  3. 还可以进行一些剪枝操作:确定第一个数或者第二个数后判断与target大小

16最接近的三数之和

  1. 三重循环，暴力破解
  2. 排序，三重循环，判断a+b+c与target的大小，移动b和c，需要记录一个最佳答案

15三数之和

  1. 先排序，然后双指针
    • 三重循环，第一层不变，第二层向右，第三层向左(第三层可以通过target减少步骤)
    • 时间:O(n的平方)、空间:O(logn)——排序

11盛水最多的容器

  1. 双指针，每次移动较小的，并记录盛水量。

4两个正序数组中位数

  1. 二分查找:转化成寻找两个有序数组中的第 k 小的数，其中 k为 (m+n)/2或 (m+n)/2+1。

    • 比较 A[k/2-1]和B[k/2-1]
    • 三种情况，舍弃小的那一边，更新k
    • 处理特殊情况:越界，空数组，k为1
    • 边界情况+正常情况

  2. 暴力:合并+排序

2无重复字符的最长子串

  1. 滑动窗口：左右指针判断从每个字符开始的最长无重复子串，判断重复字符:哈希表hashset
  2. 动态规划：dp[ i ]表示以i位置结尾的子串的最长长度

1.二叉树根节点到叶子节点所有路径和

59螺旋矩阵 II（?）

209长度最小的子数组（?）

  1. 滑动窗口：遍历过程找中，循环右边界，当sum大于target时，不断缩小左边界

十二、单调栈

1.使用场景：通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。
2.单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素大的元素，优点是只需要遍历一次。

739.每日温度（未完成）

  1. 单调栈里存放的元素：单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取
  2. 单调栈里元素是递增：注意一下顺序为从栈头到栈底的顺序
  3. 三个判断条件
    • 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况：入栈
    • 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况：入栈
    • 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况：弹出栈顶元素
  4. 使用result数组记录弹出的结果

496.下一个更大元素 I

  1. 暴力求解法
  2. 单调栈：
    • 数组result来存放结果：初始化为-1
    • 没有重复元素，我们就可以用map来做映射了。根据数值快速找到下标，还可以判断nums2[i]是否在nums1中出现过。存放nums1的元素
    • 栈头到栈底的顺序，要从小到大，也就是保持栈里的元素为递增顺序。只要保持递增，才能找到右边第一个比自己大的元素。栈里面存放下标
    • 遍历nums2中的元素。
    • 情况一：当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况：此时满足递增栈（栈头到栈底的顺序），所以直接入栈。
    • 情况二：当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况：如果相等的话，依然直接入栈，因为我们要求的是右边第一个比自己大的元素，而不是大于等于！
    • 情况三：当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况：此时如果入栈就不满足递增栈了，这也是找到右边第一个比自己大的元素的时候。

503.下一个更大元素II

  1. 栈存放nums中元素的下标，result存放结果
  2. 遍历nums中的元素，拼接两个nums，达到496的效果

十三、每日一题

436寻找右区间（未完成）

  1. 看不懂题目

462最少移动次数使数组元素相等 II（未完成）

  1. 排序：先排序数组，需要变成的数字为x = nums[n / 2]
  2. 快速选择：求解数组第 k小元素可以使用快速选择算法，使用该算法求x

668乘法表中第k小的数（未完成）

  1. 二分查找

953验证外星语词典

  1. 同剑指 Offer II 034. 外星语言是否排序

面试题 04.06. 后继者

  1. 中序遍历
  2. 二分搜索的树版本：记录大于target的最小节点

812最大三角形面积（未完成）

  1. 枚举：使用行列式计算三角形面积，每次取三个点需要三重循环
  2. 凸包：

面试题 01.05. 一次编辑（未完成）

  1. 分情况讨论：
    • first 和 second 需要一次编辑：|m-n|1,且下标不相等位置之差小于等于1，或者mn,且只有一个字符不同
    • first 和 second 需要零次编辑：m=n 且 first 和 second 相等

944删列造序

  1. 直接遍历即可

626换座位（未完成）

449序列化和反序列化二叉搜索树（未完成）

  1. 后序遍历：
    • 序列化时，只需要对二叉搜索树进行后序遍历，再将数组编码成字符串即可。
    • 反序列化时，需要先将字符串解码成后序遍历的数组，将后序遍历的数组恢复成二叉搜索树（利用性质）

433最小基因变化（未完成）

  1. 广度优先搜索
    • 相当于遍历，每此可能的变化种类是树的一层，使用层次遍历，每次记录当前字符下次可能变化的种类，并记录步数（层数）
    • 数据结构：两个哈希集合记录bank中数据和已经变化的种类，一个队列进行遍历
  2. 预处理优化

1823找出游戏的获胜者

  1. 同约瑟夫环

868二进制间距

  1. 位运算：用一个变量 last 记录上一个找到的 1 的位置；n = n >> 1，这样在第 i 步时，n & 1 （获取 n的最低位）得到的就是初始 n 的第 i个二进制位

479最大回文数乘积

  1. 从大到小枚举回文数，由于确定了回文数的左半部分，其右半部分也就确定了，因此我们只需要枚举左半部分。
  2. 将数字翻转到其右半部分，构造回文数
  3. 然后判断n范围内有无其因子

969.煎饼排序

  1. 设一个元素的下标是 index，我们可以通过两次煎饼排序将它放到尾部：
    • 第一步选择 k = index+1，然后反转子数组 arr[0...k−1]，此时该元素已经被放到首部。
    • 第二步选择 k = n，其中 n 是数组 arr 的长度，然后反转整个数组，此时该元素已经被放到尾部。
  2. 将当前数组的最大值放到尾部，然后处理新数组，直到原数组已经完成排序，总操作数是 2×(n−1)。

838.推多米诺

  1. 广度优先搜索：用一个队列 qq 模拟搜索的顺序；数组 \textit{time}time 记录骨牌翻倒或者确定不翻倒的时间，翻倒的骨牌不会对正在翻倒或者已经翻倒的骨牌施加力；数组 \textit{force}force 记录骨牌受到的力，骨牌仅在受到单侧的力时会翻倒。

  2. 模拟：枚举所有连续的没有被推动的骨牌，根据这段骨牌的两边骨牌（如果有的话）的推倒方向决定这段骨牌的最终状态

    • 如果两边的骨牌同向，那么这段连续的竖立骨牌会倒向同一方向。

    • 如果两边的骨牌相对，那么这段骨牌会向中间倒。

    • 如果两边的骨牌相反，那么这段骨牌会保持竖立。

    • 特别地，如果左侧没有被推倒的骨牌，则假设存在一块向左倒的骨牌；如果右侧没有被推倒的骨牌，则假设存在一块向右倒的骨牌。这样的假设不会破坏骨牌的最终状态，并且边界情况也可以落入到上述三种情况中。

十四、剑指offer

剑指 Offer II 011. 0 和 1 个数相同的子数组（未完成）

  1. 前缀和 + 哈希表：
    • 将0视作-1
    • 遍历数组，计算每个下标的前缀和

剑指 Offer 33. 二叉搜索树的后序遍历序列（未完成）

剑指 Offer 34. 二叉树中和为某一值的路径

  1. 深度优先搜索
  2. 广度优先搜索

剑指 Offer II 010. 和为 k 的子数组（未完成）

  1. 枚举
  2. 前缀和 + 哈希表优化：

剑指 Offer II 116. 省份数量（未完成）

  1. 深度优先搜索
  2. 广度优先搜索
  3. 并查集

剑指 Offer 59 - II. 队列的最大值

  1. 暴力遍历
  2. 维护一个单调双端队列：
    • 当一个元素进入队列的时候，它前面所有比它小的元素就不会再对答案产生影响。
    • 从队列尾部插入元素时，提前取出队列中所有比这个元素小的元素，使得队列中只保留对结果有影响的数字。

剑指 Offer 66. 构建乘积数组（未完成）

  1. 左右乘积列表：计算每个数字的左右元素的乘积，相邻乘积之间有递推关系
  2. 可改进空间复杂度

剑指 Offer 36. 二叉搜索树与双向链表（未完成）

  1. 使用中序遍历访问树的各节点 cur ；并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向；中序遍历完成后，最后构建头节点和尾节点的引用指向

剑指 Offer II 079. 所有子集

  1. 同78子集

剑指 Offer II 113. 课程顺序—拓扑排序（未完成）

  1. 深度优先搜索
  2. 广度优先搜素

剑指 Offer 56 - I. 数组中数字出现的次数（未完成）

  1. 暴力遍历
  2. 分组异或：任选一个不为 0 的 x_i ，按照第 i 位给原来的序列分组

剑指 Offer II 085. 生成匹配的括号

  1. 同22括号生成

剑指 Offer 48. 最长不含重复字符的子字符串

  1. 同2最长不含重复字符的子字符串

剑指 Offer 44. 数字序列中某一位的数字（未完成）

  1. 找规律

剑指 Offer 64. 求1+2+…+n（未完成）

  1. 递归：利用逻辑运算符&&的短路性质
  2. 快速乘：

剑指 Offer II 021. 删除链表的倒数第 n 个结点

  1. 同19删除链表的倒数第n个节点

剑指 Offer II 041. 滑动窗口的平均值

  1. 队列：使用队列作为数据结构，记录队列长度

剑指 Offer II 075. 数组相对排序（未完成）

剑指 Offer II 072. 求平方根（未完成）

  1. 袖珍计算器算法
  2. 二分查找
  3. 牛顿迭代

剑指 Offer II 069. 山峰数组的顶部（未完成）

  1. 枚举遍历
  2. 二分查找

剑指 Offer II 068. 查找插入位置

  1. 二分查找：最后未找到就返回low的位置

剑指 Offer II 059. 数据流的第 K 大数值（未完成）

  1. 优先队列：PriorityQueue

剑指 Offer II 056. 二叉搜索树中两个节点之和（未完成）

  1. 深度优先搜索 + 哈希表
  2. 广度优先搜索 + 哈希表
  3. 深度优先搜索 + 中序遍历 + 双指针
  4. 迭代 + 中序遍历 + 双指针

剑指 Offer II 052. 展平二叉搜索树

  1. 中序遍历之后生成新的树
  2. 在中序遍历的过程中改变节点指向（未完成）

剑指 Offer II 042. 最近请求次数

  1. 使用队列作为数据结构

剑指 Offer II 034. 外星语言是否排序

  1. 记录字符顺序中字母位置，每次判断相邻的word是否符合要求

剑指 Offer II 023. 两个链表的第一个重合节点

  1. 同7链表相交

剑指 Offer II 012. 左右两边子数组的和相等

  1. 记数组的全部元素之和为 total，当遍历到第 i 个元素时，设其左侧元素之和为 sum，则其右侧元素之和为 total−nums[i]−sum。
  2. 左右侧元素相等即为 sum=total−nums[ i ] −sum，即 2×sum+nums[ i ]=total

剑指 Offer II 088. 爬楼梯的最少成本

  1. 746最小花费爬楼梯

剑指 Offer II 001. 整数除法（未完成）

剑指 Offer 68 - II. 二叉树的最近公共祖先

  1. 同236二叉树的最近公共祖先

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先（未完成）

  1. 两次遍历：获取节点路径，依次比较路径中节点，到“分叉点”的时候即为最近公共祖先
  2. 一次遍历：
    • 如果当前节点的值大于 p 和 q 的值，说明 p 和 q 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；
    • 如果当前节点的值小于 p 和 q 的值，说明 p 和 q 应该在当前节点的右子树，因此将当前节点移动到它的右子节点；
    • 如果当前节点的值不满足上述两条要求，那么说明当前节点就是「分岔点」

883三维形体投影面积

  1. 高处看是数组元素个数，侧面看是每行最大值，正面看是每列最大值

剑指 Offer 55 - II. 平衡二叉树

  1. 自顶向下的递归：从根节点起，先求深度，然后判断平衡
  2. 自底向上的递归：求深度的时候就判断平衡

剑指 Offer 58 - I. 翻转单词顺序

  1. ​ 使用split切割，然后使用StringBuilder拼接

剑指 Offer 55 - I. 二叉树的深度

  1. 递归
  2. 层序遍历

剑指 Offer 57 - II. 和为s的连续正数序列

  1. 回溯法：注意使用已经遍历的数组，要求结果连续
  2. 双指针：left和right区间遍历

剑指 Offer 10- I. 斐波那契数列

  1. 迭代或者递归

剑指 Offer 62. 圆圈中最后剩下的数字（未完成）

  1. 数学 + 递归：最终会留下第几个元素，设为 x = f(n - 1, m)；n==1时，返回0
  2. 数学 + 迭代

剑指 Offer 65. 不用加减乘除做加法（未完成）

  1. 位运算：无进位和 与 异或运算 规律相同，进位 和 与运算 规律相同（并需左移一位）；（和 s ）==（非进位和 n ）++（进位 c ）；循环求 n 和c ，直至进位 c=0 ；此时 s=n ，返回 n 即可。

剑指 Offer 16. 数值的整数次方

  1. 快速幂 + 递归：
    • 当我们要计算 x^n时，我们可以先递归地计算出 y = x^⌊n/2⌋；
    • 根据递归计算的结果，如果 n 为偶数，那么 x^n = y^2 ；如果 n 为奇数，那么 x^n = y^2×x
    • 递归的边界为 n = 0，任意数的 0 次方均为 1。
  2. 快速幂 + 迭代：
    • 贡献的指数部分：恰好就对应了 7777 的二进制表示 (1001101)_2(1001101)2 中的每个 11！
    • 如果 N 二进制表示的最低位为 1，那么需要计入贡献
    • 每次到1就把累计的贡献乘入

剑指 Offer 15. 二进制中1的个数（未完成）

  1. 循环检查二进制位：当检查第 i位时，我们可以让 n 与 2^i进行与运算，当且仅当 n的第 i位为 1 时，运算结果不为 0。（n & (1 << i)）
  2. 位运算优化：n & (n−1)，其预算结果恰为把 n 的二进制位中的最低位的 1 变为 0 之后的结果

剑指 Offer 13. 机器人的运动范围（未完成）

  1. 广度优先搜索：每次向下或者向右进行，遍历过的点需要标记
  2. 递推：

剑指 Offer 12. 矩阵中的路径（未完成）

  1. 深度优先搜索（DFS）+ 剪枝：
    • 递归参数： 当前元素在矩阵 board 中的行列索引 i 和 j ，当前目标字符在 word 中的索引 k 。
    • 终止条件：
      1. 返回 false ： (1) 行或列索引越界 或 (2) 当前矩阵元素与目标字符不同 或 (3) 当前矩阵元素已访问过 （ (3) 可合并至 (2) ） 。
      2. 返回 true ： k = len(word) - 1 ，即字符串 word 已全部匹配。
    • 递推工作
      1. 标记当前矩阵元素： 将 board[i][j] 修改为 空字符 '' ，代表此元素已访问过，防止之后搜索时重复访问。
      2. 搜索下一单元格： 朝当前元素的 上、下、左、右四个方向开启下层递归，使用或连接 （代表只需找到一条可行路径就直接返回，不再做后续 DFS ），并记录结果至 res 。
      3. 还原当前矩阵元素： 将 board[i][j] 元素还原至初始值，即 word[k] 。

剑指 Offer 09. 用两个栈实现队列

  1. 两个栈s1和s2
  2. 入队：直接压入s1
  3. 出队：若s2不空，直接s2出栈；否则若s1不空，将s1元素压入s2，再从s2出栈；否则返回-1

剑指 Offer 30. 包含min函数的栈

  1. 数据栈 A ： 栈 A 用于存储所有元素，保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。
  2. 辅助栈 B ： 栈 B 中存储栈 A 中所有 非严格降序 的元素，则栈 A 中的最小元素始终对应栈 B 的栈顶元素，即 min() 函数只需返回栈 B 的栈顶元素即可。
  3. 只需设法维护好 栈 B 的元素，使其保持非严格降序，即可实现 min() 函数的 O(1) 复杂度

剑指 Offer 06. 从尾到头打印链表

  1. 使用栈，然后逆向输出

剑指 Offer 24. 反转链表

  1. 头插法，先建立空头结点

剑指 Offer 35. 复杂链表的复制（深拷贝）

  1. 方法一：回溯 + 哈希表：利用回溯的方式，让每个节点的拷贝操作相互独立。
    • 对于当前节点，首先要进行拷贝；
    • 然后我们进行「当前节点的后继节点」和「当前节点的随机指针指向的节点」拷贝；
    • 拷贝完成后将创建的新节点的指针返回，即可完成当前节点的两指针的赋值。
  2. 方法二：迭代 + 节点拆分
    • 对于链表 A→B→C，我们可以将其拆分为 A→A ′→B→B ′→C→C ′ 。
    • 找到每一个拷贝节点 S' 的随机指针应当指向的节点，即为其原节点 S 的随机指针指向的节点 T 的后继节点 T' 。需要注意原节点的随机指针可能为空。
    • 将这个链表按照原节点与拷贝节点的种类进行拆分，只需要遍历一次。同样需要注意最后一个拷贝节点的后继节点为空。

剑指 Offer 05. 替换空格

剑指 Offer 53 - I. 在排序数组中查找数字

  1. 第一个等于 target 的位置leftIdx，第一个大于 target 的位置减一rightIdx，当target 在数组中存在时，target 在数组中出现的次数为rightIdx−leftIdx+1。
  2. 寻找 leftIdx 即为在数组中寻找第一个大于等于 target 的下标，寻找rightIdx 即为在数组中寻找第一个大于 target 的下标
  3. 暴力解法：遍历

剑指 Offer 53 - II. 0～n-1中缺失的数字

  1. 计算中点 m = (i + j) // 2 ，其中 "//" 为向下取整除法；

  2. 若 nums[m]=m ，则 “右子数组的首位元素” 一定在闭区间 [m + 1, j] 中，因此执行 i = m + 1；

  3. 若 nums[m] =m ，则 “左子数组的末位元素” 一定在闭区间 [i, m - 1] 中，因此执行 j = m - 1；

剑指 Offer 04. 二维数组中的查找

  1. 从二维数组的右上角开始查找
  2. 如果当前元素等于目标值，则返回 true
  3. 如果当前元素大于目标值，则移到左边一列
  4. 如果当前元素小于目标值，则移到下边一行

剑指 Offer 11. 旋转数组的最小数字

  1. 考虑数组中的最后一个元素 x：在最小值右侧的元素，它们的值一定都小于等于 x；而在最小值左侧的元素，它们的值一定都大于等于 x
  2. numbers[pivot]<numbers[high]。这说明 numbers[pivot] 是最小值右侧的元素，忽略二分查找区间的右半部分。
  3. numbers[pivot]>numbers[high]。这说明 numbers[pivot] 是最小值左侧的元素，忽略二分查找区间的左半部分。
  4. numbers[pivot]==numbers[high]，由于重复元素的存在，我们并不能确定numbers[pivot] 究竟在最小值的左侧还是右侧，唯一可以知道的是，由于它们的值相同，所以无论 numbers[high] 是不是最小值，都有一个它的「替代品」numbers[pivot]，因此可以忽略二分查找区间的右端点。
  5. 二分查找：int pivot = low + (high - low) / 2;防止high + low)直接溢出了

剑指 Offer 50. 第一个只出现一次的字符

  1. 方法一：使用哈希表存储频数：对字符串进行两次遍历。在第一次遍历时，使用哈希映射统计出字符串中每个字符出现的次数。在第二次遍历时，只要遍历到了一个只出现一次的字符，那么就返回该字符，否则在遍历结束后返回空格。
  2. 方法二：使用哈希表存储索引：
    • 哈希映射中，键表示一个字符，值表示它的首次出现的索引（如果该字符只出现一次）或者 -1（如果该字符出现多次）。
    • 第一次遍历字符串，c 不在哈希映射中，将 它的索引作为一个键值对加入哈希映射中，否则我们将 c在哈希映射中对应的值修改为 -1。
    • 再遍历一次哈希映射中的所有值，找出其中不为 -1 的最小值，如果哈希映射中的所有值均为 -1，返回空格。
  3. 方法三：队列：
    • 使用与方法二相同的哈希映射，并且使用一个额外的队列
    • 设当前遍历到的字符为 c，如果 c不在哈希映射中，我们就将 c 与它的索引作为一个二元组放入队尾
    • 否则就需要检查队列中的元素是否都满足「只出现一次」的要求，即我们不断地根据哈希映射中存储的值（是否为 -1）选择弹出队首的元素，直到队首元素「真的」只出现了一次或者队列为空。

面试题32 - I. 从上到下打印二叉树

  1. 层序遍历

剑指 Offer 32 - II. 从上到下打印二叉树 II

  1. 层序遍历

剑指 Offer 32 - III. 从上到下打印二叉树 III

  1. 方法一：层序遍历 + 双端队列：使用LinkList双端队列，根据结果List的size判断层数
    • 奇数层 则添加至 tmp 尾部 ，tmp.addLast(node.val)
    • 偶数层 则添加至 tmp 头部 ，tmp.addFirst(node.val)
  2. 方法二：层序遍历 + 双端队列（奇偶层逻辑分离）：将奇偶层逻辑拆分，可以消除冗余的判断，每次处理一个奇一个偶
  3. 方法三：层序遍历 + 倒序：Collections.reverse(tmp);倒序函数

剑指 Offer 26. 树的子结构

  1. 先序遍历树 A 中的每个节点，对应函数 isSubStructure(A, B)

    • 特例处理： 当 树 A 为空 或 树 B 为空 时，直接返回 false ；
    • 返回值： 若树 B 是树 A 的子结构，则必满足以下三种情况之一，因此用或 || 连接；
      以 节点 A 为根节点的子树 包含树 B ，对应 recur(A, B)；
      树 B 是 树 A 左子树 的子结构，对应 isSubStructure(A.left, B)；
      树 B 是 树 A 右子树 的子结构，对应 isSubStructure(A.right, B)；

  2. 判断树A中 以每个节点为根节点的子树是否包含树B ，对应函数 recur(A, B)

    • 终止条件：
      当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true ；
      当节点 A 为空：说明已经越过树 A 叶子节点，即匹配失败，返回 false ；
      当节点 A 和 B 的值不同：说明匹配失败，返回 false ；

    • 返回值：
      判断 A 和 B 的左子节点是否相等，即 recur(A.left, B.left) ；
      判断 A 和 B 的右子节点是否相等，即 recur(A.right, B.right) ；

剑指 Offer 27. 二叉树的镜像

  1. 递归：先镜像左右子树，然后交换左右子树。
  2. 辅助栈（或队列）：广度优先遍历树，每次交换遍历到的节点的左右子树。

面试题28. 对称的二叉树

  1. 递归：节点的左子树与右子树对称

十五、双指针

剑指 Offer II 018. 有效的回文

  1. 双指针：遍历+判断
  2. 筛选 + 判断：
    • 对字符串 s 进行一次遍历，并将其中的字母和数字字符进行保留
    • 判断：逆序、双指针

剑指 Offer II 006. 排序数组中两个数字之和

  1. 双指针：left和right，计算和与target比较，然后移动指针
  2. 二分查找：在数组中找到两个数，使得它们的和等于目标值，可以首先固定第一个数，然后寻找第二个数

剑指 Offer 57. 和为s的两个数字

  1. 两个指针分别前后遍历，符合要求就返回，否则返回空数组

剑指 Offer 22. 链表中倒数第k个节点

  1. 双指针：先前进k个，然后两个指针一起前进，直到最后

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

  1. 双指针：注意循环条件为low<high；类似一轮快速排序

34在排序数组中查找元素的第一个和最后一个位置

  1. 二分查找：查找大于等于target的第一个位置作为left，大于target的第一个位置作为right，然后减一，最后验证两个值是否符合要求。

剑指 Offer 25. 合并两个排序的链表

  1. 采用两个指针遍历两个链表，逐个比较大小，然后连接到新链表上

142环形链表 II

  1. 设置fast和slow指针，若存在环，则两个指针会在环中相遇，此时从头节点到环入口的距离等于相遇点到环入口的距离。
  2. 哈希表：遍历链表中的每个节点，并将它记录下来；一旦遇到了此前遍历过的节点，就可以判定链表中存在环。

面试题 02.07. 链表相交

  1. 设置两个指针，根据长度需要抵达同一出发点，然后一起前进，若两个指针相同了，则可求出相交点的位置。

19删除链表的倒数第 N 个结点

  1. 一个指针先前进n个，然后第二个指针一起前进，若第一个指针到达最后，则第二个指针的位置就是所求的位置

206反转链表

  1. 头插法实现

151颠倒字符串中的单词（未完成）

  1. 使用split函数划分，然后倒序组合

剑指 Offer 05替换空格

  1. 设置原数组长度三倍长的数组，两个数组依次遍历，遇到空格则替换

344反转字符串

  1. 一个前指针，一个后指针，两个互相交换

27移除元素

  1. 一个指针指向遍历的元素，一个指向当前可插入的位置

十六、BFS+DFS

386字典序排数（未完成）

  1. 深度优先搜索：
    • 尝试在 \number 后面附加一个零，即number×10，如果 number×10≤n，那么说明 umber×10 是下一个字典序整数；
    • 如果 numbermod10=9 或 number+1>n，那么说明末尾的数位已经搜索完成，退回上一位，即number/10向下取整，然后继续判断直到number mod 10!=9 且 number+1≤n 为止，那么number+1 是下一个字典序整数。

207课程表（未完成）

  1. BFS
  2. DFS

每日一题

744寻找比目标字母大的最小字母：二分查找。

307区域和检索 - 数组可修改（未完成）：分块处理、线段树、树状数组。

357统计各位数字都不同的数字个数：排列组合，每一位数字是除去前几位已经出现的数字的可能选择。

806写字符串需要的行数：遍历计算

780到达终点（未完成）：困难题

954二倍数对数组（未完成）：采用哈希表+按绝对值排序的排序算法

4两个正序数组的中位数（未完成）：

面试题

  1. 有一个大文件，存了很多ip，怎么找到数量第K多的ip？
    • 先哈希分片，用一个map去统计每一个分片中相同IP的数量，再转成数组，找第K大的数。
    • 算法题：给一个hashmap（key：ip；value：数量），找到数量第K多的ip。
  2. 字符串规则：空格，大小写字母。 有字符串a和字符串b，在去掉空格和忽略大小写之后，判断两个字符串是否相等。
  3. 中文拼音数字串和英文数字串互相转换，其中Double后面只能跟英文数字，如果是跟中文数字返回Err。
  4. .一个无序数组，你怎么判断这个数组的元素是连续不重复的
  5. 人狼羊过河问题
  6. 给定二维数组，按照主对角线输出元素
  7. 三门问题：山羊和汽车

进度：第二遍

  1. 动态规划完成
  2. 贪心算法完成
  3. 数组完成
  4. 链表完成
  5. 开始哈希表：3
posted @ 2021-12-20 13:04  汤十五  阅读(152)  评论(0)    收藏  举报