CF1266F

来一个 $O(nlogn)$ 做法，跑得挺快。

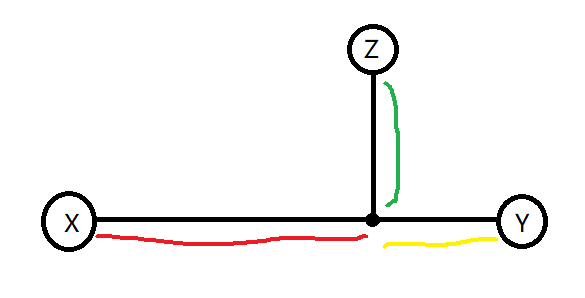
假设点集 $S$ 包含点 $X,Y,Z$ ，红色链长度为 $a$ ，黄色链长度为 $b$ ，绿色链长度为 $c$ 。

如果 $|a-b|>1$ ，那么有 $|dis(X,Z)-dis(Y,Z)|=|(a+c)-(b+c)|=|a-b|>1$ ，不符合题目要求。

所以 $a=b$ 或 $|a-b|=1$ 。所以存在一个点 $A$ ，到 $S$ 中每一个点的距离都为 $p$ 或 $p+1(0<2p<n)$ 。

接着发现一定是一下两种情况之一（证明留给读者自行思考）：

情况1： $S$ 中任两点到点 $A$ 的链没有公共边。

情况2： $S$ 中任意一点 $P$ 满足 $\text{min}(dis(P,A),dis(P,A'))=p$ （ $A'$ 为一个与 $A$ 相邻的点）。

于是， $S$ 中的点便是由 $A$ 点或者 $A$ 点及 $A'$ 点伸出来的若干条“长度相近”链的另一端点组成（如图）。

其中“长度相近”指长度均为 $p$ 或 $p+1$ ，且长度为 $p$ 的链只有一条或长度为 $p+1$ 的链只有一条。

预处理出每一个点连出所有边引出链的最大长度，对于一个点 $P$ ，设其引出第 $k$ 长的链长度为 $len(p,k)$ ，则$ans_{len(p,k)} \geq k$。

又因为 $ans_x \geq ans_{x+2}$ ，所以可以先对于每个 $k$ ，求出最大的 $x$ 使 $ans_x \geq k$ ，再做一边后缀最大值。

先枚举其中一个中心点，再枚举其引出的一条边，设k为这条边引出链的最大长度，一共可以引出 $d$ 条长度为 $k$ 的链。

那么执行 $ans[k]=max(ans[k],d)$ 。对每个点，将其引出链按最大长度排序即可求得 $d$ 和 $k$ 。

这样一个中心点的情况就搞定了。

对于点 $i$ ，设集合 $S_i$ 中有 $deg_i$ 个元素，分别为 $i$ 引出 $deg_i$ 条边所引出链长度的最大值。

枚举其中一个中心点 $P$ ，设另一个为 $Q$ ，则 $P,Q$ 相邻。我们只需要对于每一个 $S_{P,j}(0 \leq j<deg_P)$ ，找到点 $Q$ ，使集合 $S_P,S_Q$ 中大于 $S_{P,j}$ 的数最多。因为每个数相当于一条链的长度。把问题离线下来（按照 $S_{P,j}$ 从大到小排序），用bfs序把与 $P$ 相邻的点转化为一段区间以及 $fa_P$ ，然后写一个支持单点加，区间最大值的线段树即可。具体见代码吧。

#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n,cnt=-1,temp,qcnt=0;
int deg[500000],l1[500000],l2[500000];
int fir[500000],to[1000000],nxt[1000000];
int fa[500000],ans[500000],f[500000];
int id[500000],mx[2000000],o[500000];
vector<int> len[500000];
struct query{
    int x,val,o;
}qu[1000000];
inline bool comp(query q1,query q2)
{
    return q1.val>q2.val;
}
inline void Add(int a,int b,int c)
{
    qu[qcnt].x=a;
    qu[qcnt].val=c;
    qu[qcnt++].o=b;
    return;
}
inline void add(int a,int b)
{
    to[++cnt]=b;
    nxt[cnt]=fir[a];
    fir[a]=cnt;
    deg[b]++;
    return;
}

void dfs1(int i,int f)
{
    fa[i]=f;
    for(int j=fir[i];j!=-1;j=nxt[j]){
        if(to[j]==f)
            continue;
        dfs1(to[j],i);
        l1[i]=max(l1[i],l1[to[j]]);
    }
    l1[i]++;
    return;
}
void dfs2(int i,int l)
{
    l2[i]=l;
    int mx1=0,mx2=0;
    for(int j=fir[i];j!=-1;j=nxt[j]){
        temp=to[j];
        if(temp==fa[i])
            continue;
        if(mx1<l1[temp]){
            mx2=mx1; mx1=l1[temp];
        }
        else if(mx2<l1[temp])
            mx2=l1[temp];
    }
    for(int j=fir[i];j!=-1;j=nxt[j]){
        temp=to[j];
        if(temp==fa[i])
            continue;
        if(mx1==l1[temp])
            dfs2(temp,max(mx2,l2[i])+1);
        else dfs2(temp,max(mx1,l2[i])+1);
    }
    return;
}

int t1,t2;
void upd(int i,int l,int r)
{
    if(l==r){
        mx[i]++;
        return;
    }
    int mid=(l+r)>>1;
    if(t1<=mid) upd(i<<1,l,mid);
    else upd(i<<1|1,mid+1,r);
    mx[i]=max(mx[i<<1],mx[i<<1|1]);
    return;
}
inline void update(int x)
{
    t1=x; upd(1,0,n-1); f[x]++;
    return;
}
int qry(int i,int l,int r)
{
    if(t1<=l&&r<=t2)
        return mx[i];
    int mid=(l+r)>>1,res=0;
    if(t1<=mid) res=qry(i<<1,l,mid);
    if(mid<t2) res=max(res,qry(i<<1|1,mid+1,r));
    return res;
}
inline int querymax(int x,int y)
{
    t1=x; t2=y;
    return qry(1,0,n-1);
}

void bfs(void)
{
    cnt=0;
    id[0]=cnt++;
    queue<int> q;
    q.push(0);
    while(q.size()>0){
        int i=q.front();
        q.pop();
        o[i]=cnt-1;
        for(int j=fir[i];j!=-1;j=nxt[j])
            if(to[j]!=fa[i]){
                id[to[j]]=cnt++;
                q.push(to[j]);
            }
    }
    return;
}
void solve(void)
{
    for(int i=2;i<n;i++)
        ans[i]=1;
    for(int i=0;i<n;i++){
        int s=deg[i];
        for(int d=1;d<=s;d++){
            temp=len[i][s-d]*2;
            if(temp<n) ans[temp]=max(ans[temp],d);
            if(temp<=n) ans[temp-1]=max(ans[temp-1],d);
            if(temp+1<n&&d>1&&len[i][s-d+1]>len[i][s-d])
                ans[temp+1]=max(ans[temp+1],d);
        }
    }
    
    for(int i=0;i<n;i++)
        for(int d=1;d<=deg[i];d++)
            Add(i,d,len[i][deg[i]-d]);
    sort(qu,qu+qcnt,comp);
    int pos=0;
    for(int i=0;i<qcnt;i++){
        while(pos<qcnt&&qu[pos].val>=qu[i].val)
            update(id[qu[pos++].x]);
        int X=qu[i].x,D=2*qu[i].val;
        temp=querymax(o[X]+1,o[X]+deg[X]-1);
        if(X!=0) temp=max(temp,f[id[fa[X]]]);
        ans[D]=max(ans[D],temp+qu[i].o-2);
    }
    return;
}

int main(void)
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        fir[i]=-1;
    int a,b;
    for(int i=1;i<n;i++){
        scanf("%d%d",&a,&b);
        add(a-1,b-1); add(b-1,a-1);
    }
    dfs1(0,-1); dfs2(0,0); bfs();
    for(int i=1;i<n;i++){
        len[fa[i]].push_back(l1[i]);
        len[i].push_back(l2[i]);
    }
    for(int i=0;i<n;i++){
        sort(len[i].begin(),len[i].end());
        ans[1]=max(ans[1],deg[i]+1);
    }
    solve();
    for(int i=n-3;i>0;i--)
        ans[i]=max(ans[i],ans[i+2]);
    for(int i=1;i<n;i++)
        printf("%d ",ans[i]);
    printf("1\n");
    return 0;
}