实验3作业

task1.c

include <stdio.h>

char score_to_grade(int score); // 函数声明

int main() {
int score;
char grade;

while(scanf_s("%d", &score) != EOF) {
    grade = score_to_grade(score);  // 函数调用
    printf("分数: %d, 等级: %c\n\n", score, grade);
}

return 0;

}

// 函数定义
char score_to_grade(int score) {
char ans;

switch(score/10) {
case 10:
case 9:   ans = 'A'; break;
case 8:   ans = 'B'; break;
case 7:   ans = 'C'; break;
case 6:   ans = 'D'; break;
default:  ans = 'E';
}

return ans;

}

问题1：score_to_grade的功能是根据输入的分数将其转化为对应的字符
问题2：源代码中ans与char匹配，改变后ans=“A”应该是ans=‘A’

task2.c
方法1：#include <stdio.h>

int sum_digits(int n); // 函数声明

int main() {
int n;
int ans;

while(printf("Enter n: "), scanf("%d", &n) != EOF) {
    ans = sum_digits(n);    // 函数调用
    printf("n = %d, ans = %d\n\n", n, ans);
}

return 0;

}

// 函数定义
int sum_digits(int n) {
int ans = 0;

while(n != 0) {
    ans += n % 10;
    n /= 10;
}

return ans;

}
方法2：#include <stdio.h>

int sum_digits(int n); // 函数声明

int main() {
int n;
int ans;

while (printf("Enter n: "), scanf_s("%d", &n) != EOF) {
    ans = sum_digits(n);    // 函数调用
    printf("n = %d, ans = %d\n\n", n, ans);
}

return 0;

}

// 函数定义
int sum_digits(int n) {
if (n < 10)
return 0;

return sum_digits(n / 10) + n % 10;

}

问题1：sum_digits的功能是计算输入整数n的各位数字之和，通过循环取出整数个各位数字累加到ans中，直到数字变为0
问题2：能实现；原方式是迭代的算法思维，新方式是递归的算法思维

task3.c

include <stdio.h>

int power(int x, int n); // 函数声明

int main() {
int x, n;
int ans;

while(printf("Enter x and n: "), scanf("%d%d", &x, &n) != EOF) {
    ans = power(x, n);  // 函数调用
    printf("n = %d, ans = %d\n\n", n, ans);
}

return 0;

}

// 函数定义
int power(int x, int n) {
int t;

if(n == 0)
    return 1;
else if(n % 2)
    return x * power(x, n-1);
else {
    t = power(x, n/2);
    return t*t;
}

}

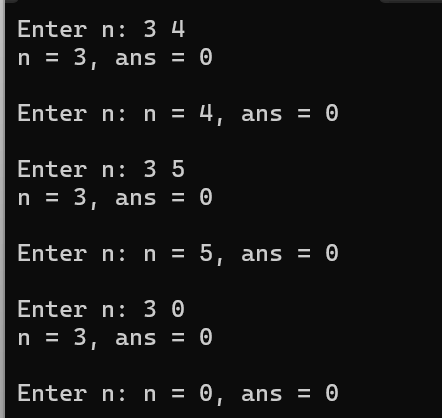
问题1：power的功能是计算x的n次幂
问题2：是递归函数；
递归模式：当n == 0时， power(x, n) = 1，递归终止。
当n % 2 != 0（n为奇数）时，power(x, n) = x * power(x, n - 1)，即将求x的n次幂转化为求x乘以x的n - 1次幂 。
当n % 2 == 0（n为偶数）时，power(x, n) = power(x, n / 2) * power(x, n / 2)，即把求x的n次幂转化为求x的n / 2次幂并将其结果平方。
数学公式模型：

task4.c

include <stdio.h>

int is_prime(int n) {
if (n <= 1) {
return 0;
}
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
return 0;
}
}
return 1;
}

int main() {
int count = 0;
printf("100以内的孪生素数有：\n");
for (int i = 3; i + 2 <= 100; i += 2) {
if (is_prime(i) && is_prime(i + 2)) {
printf("%d %d\n", i, i + 2);
count++;
}
}
printf("孪生素数的总数为：%d\n", count);
return 0;
}

task5.c

include <stdio.h>

int count = 0;

void hanoi(int n, char from, char mid, char to) {
if (n == 1) {
printf("%d: %c --> %c\n", 1, from, to);
count++;
}
else {
hanoi(n - 1, from, to, mid);
printf("%d: %c --> %c\n", n, from, to);
count++;
hanoi(n - 1, mid, from, to);
}
}

int main() {
int n;
while (scanf_s("%d", &n) != EOF) {
count = 0;
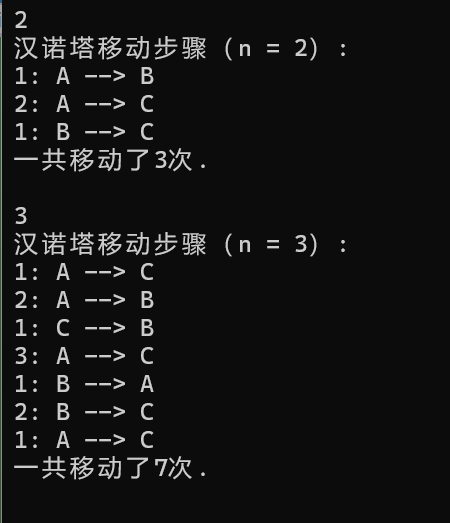
printf("汉诺塔移动步骤（n = %d）:\n", n);
hanoi(n, 'A', 'B', 'C');
printf("一共移动了%d次.\n\n", count);
}
return 0;
}

task6.c
迭代方式：

include <stdio.h>

int func(int n, int m); // 函数声明

int main() {
int n, m;
int ans;

while(scanf_s("%d%d", &n, &m) != EOF) {
    ans = func(n, m);   // 函数调用
    printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
}
    
return 0;

}
int func(int n, int m) {
if (m > n) {
return 0;
}
if (m == 0 || m == n) {
return 1;
}
int numerator = 1;
int denominator = 1;
for (int i = 1; i <= m; i++) {
numerator *= (n - (m - i));
denominator *= i;
}
return numerator / denominator;
}
递归函数：

include <stdio.h>

int func(int n, int m); // 函数声明

int main() {
int n, m;
int ans;

while(scanf_s("%d%d", &n, &m) != EOF) {
    ans = func(n, m);   // 函数调用
    printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
}
    
return 0;

}
int func(int n, int m) {
if (m > n) {
return 0;
}
if (m == 0 || m == n) {
return 1;
}
return func(n - 1, m) + func(n - 1, m - 1);
}

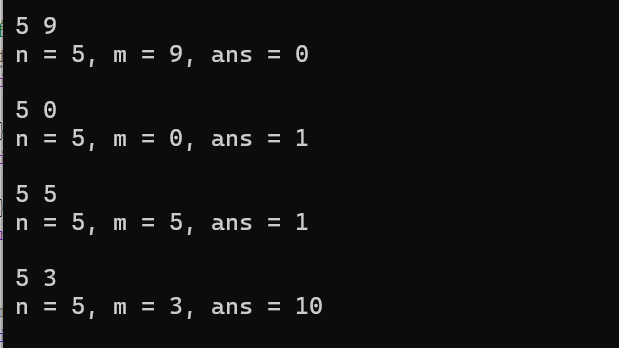
task7.c

include <stdio.h>

// 函数声明
int gcd(int a, int b, int c);

int main() {
int a, b, c;
int ans;
while (scanf_s("%d%d%d", &a, &b, &c) != EOF) {
ans = gcd(a, b, c); // 函数调用
printf("最大公约数: %d\n\n", ans);
}
return 0;
}

// 函数定义
int gcd(int a, int b, int c) {
int min_num = a;
if (b < min_num) {
min_num = b;
}
if (c < min_num) {
min_num = c;
}
for (int i = min_num; i >= 1; i--) {
if (a % i == 0 && b % i == 0 && c % i == 0) {
return i;
}
}
return 1;
}

实验总结：
在本次实验中，深入理解了函数声明、定义和调用的流程，明确函数声明要在调用前。掌握了迭代和递归两种重要的算法思维。