并查集

例题一：合并集合：

 

 

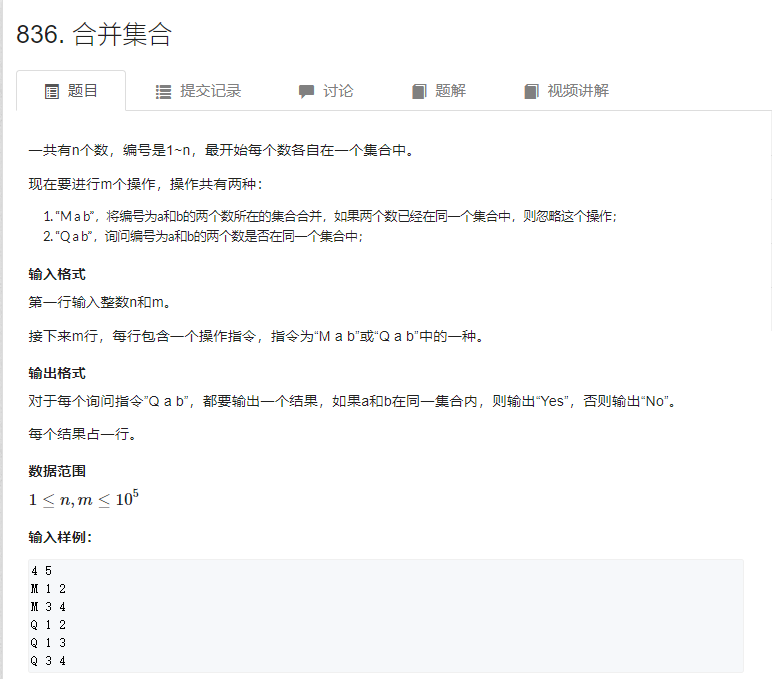
#include<iostream>

using namespace std;

const int N=100010;

int a[N],p[N];
int n,m;

int find(int x)
{
    if(p[x]!=x) p[x]=find(p[x]);
    
    return p[x];
}
f
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        p[i]=i;
    }
    while(m--)
    {
        char op;
        cin>>op;
        if(op=='M')
        {
            int x,y;
            cin>>x>>y;
            if(find(x)!=find(y)) p[find(x)]=find(y);
            
        }
        else
        {
            int x,y;
            cin>>x>>y;
            if(find(x)==find(y))
                puts("Yes");
            else
                puts("No");
        }
    }
    
    return 0;
}

 

 

 

例题二：用并查集维护信息

 

 

只要我们知道每个点和根节点的关系，就知道任意俩个点之间的关系。

可以用每个点到根节点的距离来表示关系： 1 （吃根节点） 2（吃1  被根节点吃） 3 （同类） mod 3  余1（吃根节点，吃余0） 余2（被根节点吃，吃余1）  余0（和根节点同类，吃余2）

 

 

 

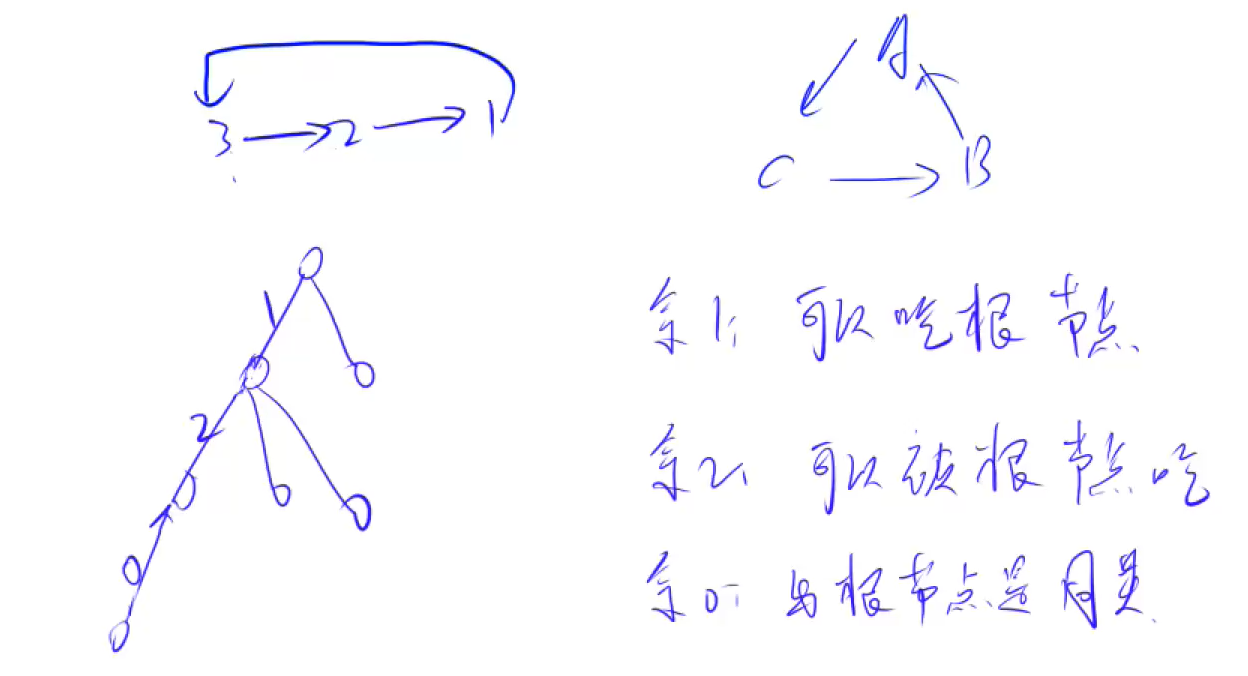
距离的含义： x吃y （y到x的距离为1）

 我们只能记录每一个点到根节点的距离（每次求完一次并查集都会做路劲压缩，将到父节点的距离改成到根节点的距离）

 

这就好比公司里每个人的等级：要判断每个人直接的等级，只需要记录每个人与领袖之间的等级就可以知道各个人直接的关系。

 

#include <iostream>

using namespace std;
const int N=500010;
int p[N],d[N];
int n,m;


//并查集
int find(int x)
{
    if(p[x]!=x)
    {
        int t=find(p[x]);
        d[x]+=d[p[x]];
        p[x]=t;
    }
    return p[x];
}



int main()
{
    cin>>n>>m;
    
    for(int i=1;i<=n;i++) p[i]=i;
    
    int res=0;
    
    while(m--){
        int t,x,y;
        cin>>t>>x>>y;
        
        if(x>n || y>n)
        {
            res++;
        }
        else{
            int px=find(x),py=find(y);  //px==x的根节点 py==y的根节点
            if(t==1)
            {
                if(px==py && (d[x]-d[y])%3) res++;   //如果在同一颗树上且mod3余数不为0
                else if(px!=py)            //不在同一棵树上
                {
                    p[px]=py;           //将x连到y树上
                    d[px]=d[y]-d[x];    
                }
                
            }
            else{
                if(px==py && (d[x]-d[y]-1)%3) res++;     //xy在同一颗树上，且x-y%3==1 不成立
                else if(px!=py)
                {
                    p[px]=py;
                    d[px]=d[y]+1-d[x];    //(d[x]+？-d[y])%3==1   
                }
            }
        }
        
    }
    
    cout<<res<<endl;
    
    return 0;
    
    
}