数据结构:跳跃链表
关注公众号,一起交流,微信搜一搜: 潜行前行
什么是跳跃链表
开发时经常使用的平衡数据结构有B数、红黑数,AVL数。但是如果让你实现其中一种,很难,实现起来费时间。而跳跃链表一种基于链表数组实现的快速查找数据结构,目前开源软件 Redis 和 LevelDB 都有用到它。它的效率和红黑树以及 AVL 树不相上下
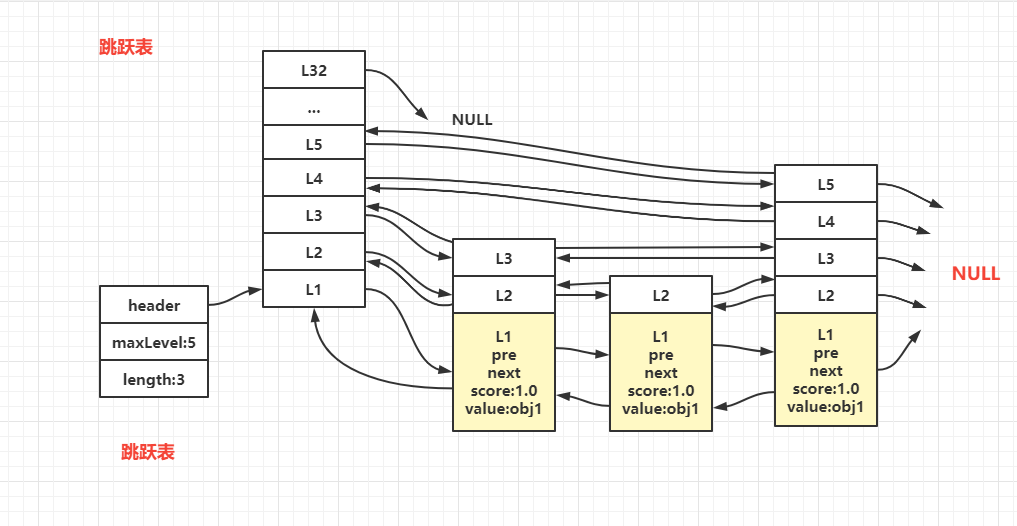
跳跃链表结构
结构
public class SkipList<T> {
//跳跃表的头尾
private SkipListNode<T> head;
//跳跃表含的元素长度
private int length;
//跳表的层数 的历史最大层数
public int maxLevel;
public SecureRandom random;
private static final int MAX_LEVEL = 31;
public SkipList() {
//初始化头尾节点及两者的关系
head = new SkipListNode<>(SkipListNode.HEAD_SCORE, null, MAX_LEVEL);
//初始化大小,层,随机
length = 0;
maxLevel = 0; // 层数从零开始计算
random = new SecureRandom();
}
...
- header:指向跳跃表的头节点
- maxLevel:记录目前跳跃表,层数最大节点的层数
- length:链表存在的元素长度
节点
跳跃链表节点的组成:前节点、后节点、分值(map的key值)、及存储对象 value
public class SkipListNode<T> {
//在跳表中排序的 分数值
public double score;
public T value;
public int level;
// 前后节点
public SkipListNode<T> next,pre;
//上下节点形成的层
public SkipListNode<T>[] levelNode;
private SkipListNode(double score, int level){
this.score = score;
this.level = level;
}
public SkipListNode(double score, T value, int level) {
this.score = score;
this.value = value;
this.level = level;
this.levelNode = new SkipListNode[level+1];
//初始化 SkipListNode 及 每一层的 node
for (int i = level; i > 0; --i) {
levelNode[i] = new SkipListNode<T>(score, level);
levelNode[i].levelNode = levelNode;
}
this.levelNode[0] = this;
}
@Override
public String toString() { return "Node[score=" + score + ", value=" + value + "]"; }
}
跳表是用空间来换时间
- 在我实现的跳跃链表节点,包括一个 levelNode 成员属性。它就是节点层。跳跃链表能实现快速访问的关键点就是它
- 平时访问一个数组,我们是顺序遍历的,而跳跃链表效率比数组链表高,是因为它使用节点层存储多级索引,形成一个稀疏索引,所以需要的更多的内存空间
跳跃链表有多快
- 如果一个链表有 n 个结点,每两个结点抽取出一个结点建立索引的话,那么第一层索引的结点数大约就是 n/2,第二层索引的结点数大约为 n/4,以此类推第 m 层索引的节点数大约为 n/(2^m)
- 访问数据时可以从 m 层索引查询定位到 m-1 层索引数据。而 m-1 大约是 m 层的1/2。也就是说最优的时间复杂度为O(log/N)
- 最差情况。在实际实现中,每一层索引是无法每次以数据数量对折一次实现一层索引。因此折中的方式,每一层的索引是随机用全量数据建一条。也就是说最差情况时间复杂度为O(N),但最优时间复杂度不变
查询
- 查询一开始是遍历最高层 maxLevel 的索引 m。按照以下步骤查询出等于 score 或者最接近 score 的左节点
- 1:如果同层索引的 next 节点分值小于查询分值,则跳到 next 节点。cur = next
- 2:如果 next 为空。或者next节点分值大于查询分值。则跳到下一层 m-1 索引,循环 2
- 循环 1、2 步骤直到访问到节点分值和查询分值一致,或者索引层为零
// SkipList
private SkipListNode<T> findNearestNode(double score) {
int curLevel = maxLevel;
SkipListNode<T> cur = head.levelNode[curLevel];
SkipListNode<T> next = cur.next;
// 和当前节点分数相同 或者 next 为 null
while (score != cur.score && curLevel > 0) {
// 1 向右 next 遍历
if (next != null && score >= next.levelNode[0].score) {
cur = next;
}
next = cur.levelNode[curLevel].next;
// 2 向下遍历,层数减1
while ((next == null || score < next.levelNode[0].score) && curLevel > 0) {
next = cur.levelNode[--curLevel].next;
}
}
// 最底层的 node。
return cur.levelNode[0];
}
public SkipListNode<T> get(double score) {
//返回跳表最底层中,最接近这个 score 的node
SkipListNode<T> p = findNearestNode(score);
//score 相同,返回这个node
return p.score == score ? p : null;
}
插入
- 如果分值存在则替换 value
- 如果分值对应节点不存在,则随机一个索引层数 level (取值 0~31)。然后依靠节点属性 levelNode 加入 0 到 level 层的索引
//SkipList
public T put(double score, T value) {
//首先得到跳表最底层中,最接近这个key的node
SkipListNode<T> p = findNearestNode(score);
if (p.score == score) {
// 在跳表中,只有最底层的node才有真正的value,只需修改最底层的value就行
T old = p.value;
p.value = value;
return old;
}
// nowNode 为新建的最底层的node。索引层数 0 到 31
int nodeLevel = (int) Math.round(random.nextDouble() * 32);
SkipListNode<T> nowNode = new SkipListNode<T>(score, value, nodeLevel);
//初始化每一层,并连接每一层前后节点
int level = 0;
while (nodeLevel >= p.level) {
for (; level <= p.level; level++) {
insertNodeHorizontally(p.levelNode[level], nowNode.levelNode[level]);
}
p = p.pre;
}
// 此时 p 的层数大于 nowNode 的层数才进入循环
for (; level <= nodeLevel; level++) {
insertNodeHorizontally(p.levelNode[level], nowNode.levelNode[level]);
}
this.length ++ ;
if (this.maxLevel < nodeLevel) {
maxLevel = nodeLevel;
}
return value;
}
private void insertNodeHorizontally(SkipListNode<T> pre, SkipListNode<T> now) {
//先考虑now
now.next = pre.next;
now.pre = pre;
//再考虑pre的next节点
if (pre.next != null) {
pre.next.pre = now;
}
//最后考虑pre
pre.next = now;
}
删除
- 使用 get 方法找到元素,然后解除节点属性 levelNode 在每一层索引的前后引用关系即可
//SkipList
public T remove(double score){
//在底层找到对应这个key的节点
SkipListNode<T> now = get(score);
if (now == null) {
return null;
}
SkipListNode<T> curNode, next;
//解除节点属性 levelNode 在每一层索引的前后引用关系
for (int i = 0; i <= now.level; i++){
curNode = now.levelNode[i];
next = curNode.next;
if (next != null) {
next.pre = curNode.pre;
}
curNode.pre.next = curNode.next;
}
this.length--; //更新size,返回旧值
return now.value;
}
使用示例
public static void main(String[] args) {
SkipList<String> list=new SkipList<>();
list.printSkipList();
list.put(1, "csc");
list.printSkipList();
list.put(3, "lwl");
list.printSkipList();
list.put(2, "hello world!");
list.printSkipList();
System.out.println(list.get(2));
System.out.println(list.get(4));
list.remove(2);
list.printSkipList();
}
欢迎指正文中错误
参考文章
- redis设计与实现
- 跳表(跳跃表,skipList)总结-java版
- 数据结构与算法——跳表


 浙公网安备 33010602011771号
浙公网安备 33010602011771号