习题解析之:计算圆周率——无穷级数法
【问题描述】
π是个超越数,圆周率的超越性否定了化圆为方这种尺规作图精确求解问题的可能性。有趣的是,π可以用无穷级数表示:
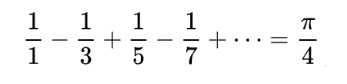
左边的展式是一个无穷级数,被称为莱布尼茨级数(Leibniz),这个级数收敛到π/4,它通常也被称为格雷戈里-莱布尼茨级数,用以纪念莱布尼茨同时代的天文学家兼数学家詹姆斯·格雷戈里。
编程用这个公式计算π值,输入一个浮点数作为阈值,当第n+1项的绝对值不大于给定阈值时停止,计算前n项的累加值,并输出得到的π值。
输入格式
一个正浮点数threshold,限定级数法求解pi值时,迭代累加时只加绝对值大于threshold的项。
输出格式
输出为一个浮点数,是程序使用级数法求解的pi值,要求保留小数点后八位。
示例
输入:
0.000002
输出:
3.14158865
【编程思路】
观察格雷戈里-莱布尼茨级数可知,级数中各项的分子恒为 1,分母是一个连续的正奇数序列。用变量 item 来保存级数的当前项的分母,初值为 1。每次循环后,item 加 2 即可。
由于级数中各项是正负交错的,为此设置一个符号位 sign,初值为 1,表示第 1 项是相加,每次循环后,sign = - sign,则 sign 的值正好按 1,-1,1,-1,…进行切换。实现级数各项正负交错的处理。
由于循环的重复次数是未知的,采用 while 循环进行处理。循环结束条件为当前项的绝对值不大于给定阈值。
按上面的思路,编写源程序如下:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号