习题解析之：二分法求函数的零点

【问题描述】

现有方程：f(x)=x⁵ − 15x⁴ + 85x³ − 225x² + 274x − 121。已知f(x)在[1.5,2.4]区间单调下降，且在该区间f(x)==0有且只有一个根，用二分法求解该根。

输入格式

输入一个正整数n，当f(x)绝对值小于10 −n时认为函数值为0

输出格式

输出方程在[1.5,2.4]区间的根，精确到小数点后第6位

示例

输入：

9

输出：

1.849016

 

【二分法的基本思想】

        二分法是一个非常高效的算法，它常常用于计算机的查找过程中。

        先玩一个小游戏。预先给定一个小于100的正整数x，让你猜，猜测过程中给予大小判断的提示，问你怎样快速地猜出来？

        这样猜测最快，先猜50，如果猜对了，结束；如果猜大了，往小的方向猜，再猜25；如果猜小了，往大的方向猜，再猜75；…，每猜测1次就去掉一半的数，就这样可以逐步逼近预先给定的数字。这种思想就是二分法。

        在用二分法进行查找时，查找对象的序列必须是有序的，即待查序列中各元素的次序是按其值的大小顺序存储的。其基本思想是先确定待查序列的范围（可用 [left,right] 区间表示），然后逐步缩小范围直到找到或找不到该记录为止。

        具体做法是：先取待查序列中间位置（mid=(left+right)/2）的数据元素与给定值比较。若相等，则查找成功；否则，若给定值比该数据元素的值小（或大），则给定值必在待查序列的前半部分[left,mid-1]（或后半部分[mid+1,right]），然后在新的查找范围内进行同样的查找。如此反复进行，直到找到数据元素值与给定值相等的元素或确定序列中没有待查找的数据为止。因此，二分查找每查找一次，或成功，或使待查找序列中元素的个数减少一半，当待查找序列中不再有数据元素时，查找失败。

      二分法查找是一种非常高效的搜索方法，主要原理是每次搜索可以抛弃一半的数据元素来缩小范围。其时间复杂度是O(log₂n)，一般用于对普通搜索方法的优化。

【本题的解题思路】

        因为在 x∈[1.5,2.4]的范围内， f(x) 随着 x的增大而减小的（单调递增）且存在零点，这就给二分法创造了条件。注意：f(1.5) > 0 且 f(2.4) < 0 。

        首先，令浮点型 left 和 right 的初值分别为1.5和2.45，然后通过比较 left 和 right 的中点 mid 处  f(x) 的数值的正负来选择子区间进行逼近。有以下两种情况：

        1）如果  f(mid) > 0，说明当前 f(mid) 与 f(left) 同号（都在 x 轴上方），此时应当在 [mid, right]的范围内继续逼近，故令   left=mid；

        2）如果 f(mid) < 0，说明当前 f(mid) 与 f(right) 同号（都在 x 轴下方），此时应当在 [left,mid] 的范围内继续逼近，故令 right=mid。

        当  f(mid) < 10⁻ⁿ 时结束，此时已经满足精度要求，即为所求的方程的根。

【源程序】

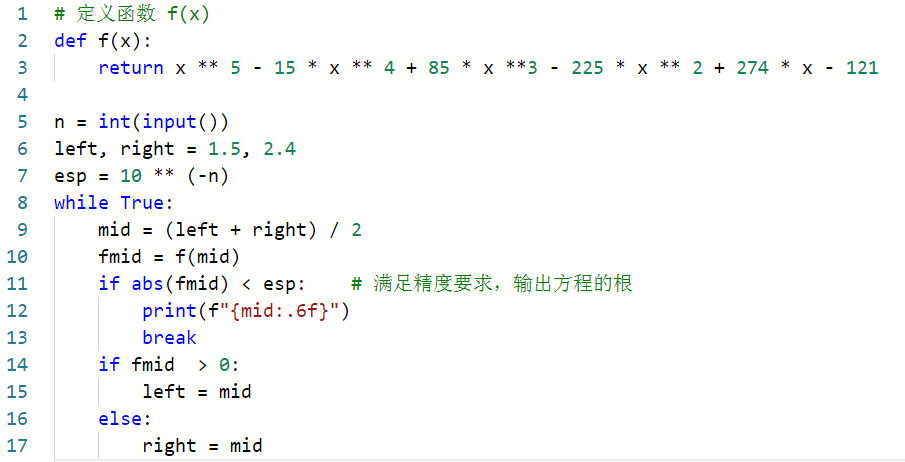
        按上述编程思路，编写源程序如下：