第六章图(6.6.2-6.6.4)
6.6.2最短路径
1.从某个源点到其余各顶点的最短路径
1.1迪杰斯特拉算法的求解过程
对于网 N=(V,E), 将 N中的顶点分成两组:
第一 组S: 已求出的最短路径的终点集合(初始时只包含源点Vo)。
第二组 V-S: 尚未求出的最短路径的顶点集合(初始时为 V- {vo})
算法将按各顶点与Vo间最短路径长度递增的次序,逐个将集合 v-s 中的顶点加入到集合S中去。在这个过程中,总保持从Vo到集合S中各顶点的路径长度始终不大千到集合 v-s 中各顶点的路径长度。
1.2迪杰斯特拉算法的实现
假设用带权的邻接矩阵arcs来表示带权有向网G,Garcs[i]Ij]表示弧<vi,vj>上的权值。若<vi,Vj>不存在,则置Garcs[i]Ij]为无穷, 源点为V0.
算法的实现要引入以下辅助的数据结构。
- 一维数组S[i]: 记录从源点Vo到终点V;是否已被确定最短路径长度, true表示确定,false表示尚未确定。
- 一维数组 Path[i]:记录从源点 Vo到终点 V;的当前最短路径上 V;的直接前驱顶点序号。其初值为:如果从 Vo到 V; 有弧,则 Path [i]为 V0;否则为— 1。
- 一维数组 D[i]: 记录从源点 Vo到终点 V;的当前最短路径长度。其初值为:如果从 V0到 Vi有弧,则 D[i)为弧上的权值;否则为 无穷。
显然,长度最短的一条最短路径必为(V0,Vk),满足以下条件: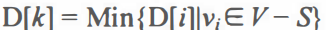
求得顶点 Vk的最短路径后,将其加入到第一组顶点集S中。
每当加入一个新的顶点到顶点集 s, 对第二组剩余的各个顶点而言,多了一个 “中转" 顶点,从而多了一个 “中转' 路径,所以要对第二组剩余的各个顶点的最短路径长度进行更新。
原来 v0到 Vi的最短路径长度为 D[i], 加进 VR之后,以Vk作为中间顶点的 "中转“ 路径长度为:D[k] + Garcs[k)[i), 若D[k] + Garcsk<D[z], 则用 D[k] + Garcsk取代 D[i]。
更新后,再选择数组D中值最小的顶点加入到第一
组顶点集S中,如此进行下去,直到图中所有顶点都加入到第一组顶点集S中为止。
1.3 算法6.10 迪杰斯特拉算法
算法步骤
1.初始化:
- 将源点 Vo加到S中,即S[v0] = true ;
- 将 v。到各个终点的最短路径长度初始化为权值,即 D[i] = Garcsv0, (vi属于V-S);
- 如果 v。和顶点v之间 有弧,则将 Vi的前驱置为 Vo, 即 Path[i] = v0 , 否则 Path[i] = -1。
2.循环n-1次,执行以下操作:
- 选择下一条最短路径的终点 Vk, 使得:D[k] = Min
- 将 Vk加到S中,即S[vk] =true;
- 根据条件更新从 v0出发到集合 v-s 上任一顶点的最短路径的长度,若条件D[k] + Gares [k] [i]<D[i]成立,则更新 D[i] = D[k] +Garcs[k] [i], 同时更改 Vi的前驱为vk; Path [i] = k。
算法描述
void ShortestPath_DIJ(AMGraph G, int vO)
{//用Dijkstra算法求有向网G的vO顶点到其余顶点的最短路径
n=G.vexnum; //n为G 中顶点的个数
for (v= O;v<n; ++v) //n个顶点依次初始化
{S[v]=false; //S初始为空集
D[v]=G.arcs[vO][v];//将vO到各个终点的最短路径长度初始化为弧上的权值
if(D[v]<Maxlnt) Path[v]=vO; //如果V0和V之间有弧,则将V的前驱置为V0
else Path[v]=-1 / /如果vO 和v之间无弧, 则将v的前驱置为一1
}
S[vO] = true; //将V0加入S
D[vO]=0;//源点到源点的距离为0
/*-----初始化结束, 开始主循环, 每次求得vO到某个顶点v的最短路径, 将v加到s集----*/
for( i=l; i<n;++i) //对其余 n-1个顶点,依次进行计算
{
min= Maxlnt;
for(w= O;w<n;++w)
if (! S [w] &&D [w] <min)
{v=w;min=D[w];}//选择一条当前的最短路径,终点为v
S[v]=true;//将v加入S
for(w=O;w<n;++w) //更新从v。出发到集合v-s上所有顶点的最短路径长度
if (! S [w) && (D [v) +G. arcs [v) [w) <D [w]))
{
D[w] =D [v] +G.arcs[v][w]; //更新 D[w]
Path[w]=v; //更改w的前驱为v
}
}
}
2.每一对顶点之间的最短路径
求解每一对顶点之间的最短路径有两种方法:其一是分别以图中的每个顶点为源点共调用n次 迪杰斯特拉算法;其二是采用下面介绍的弗洛伊德(Floyd)算法。 两种算法的时间复杂度均为O(n3 ), 但后者形式上较简单。
弗洛伊德算法仍然使用带权的邻接矩阵 arcs 来表示有向网G,求从顶点V; 到VJ的最短路径。算法的实现要引入以 下辅助的数据结构。
(1) 二维数组 Path[i] [j]:最短路径上顶点 VJ 的前一顶点的序号。
(2)二维数组D[i] [j]:记录顶点 Vi和vj之间的最短路径长度。
算法6.11费罗伊德算法
算法步骤
算法描述
void ShortestPath_Floyd(AMGraph G)
{//用Floyd算法求有向网G中各对顶点1和)之间的最短路径
for (i=O; i < G. vexnum; ++i) //各对结点之间初始已知路径及距离
for(j=O;j <G.vexnum;++j)
{
D[i][j] =G.arcs [i][j];
if(D[i] [j]<Maxint) Path[i] [j]=i; //如果i和j之间有弧,则将j的前驱置为1.
else Path[i] [j]=-1; //如果i和j之间无弧,则将j的前驱置为-1
}
for (k=O; k < G. vexnum; ++k)
for (i=O; i <G.vexnum;++i)
for(j=O;j <G.vexnum;++j)
if(D[i] [k]+D[k][j] <D[i][j])//从i经k到j的一条路径更短
{
D[i][j]=D[i][k]+D[k][j];//更新D[i][j]
Path[i][j]=Path[k][j];//更改j的前驱为K
}
}
6.6.3拓扑排序
1.AOV-网
一个无环的有向图称作有向无环图( DirectedAcycline Graph), 简称DAG图。有向无环图是描述一项工程或系统的进行过程的有效工具。通常把计划、 施工过程、 生产流程、 程序流程等都当成一个工程。除了很小的工程外,一般的工程都可分为若干个称做活动(Activity)的子工程,而这些子工程之间, 通常受着一定条件的约束, 如其中某些子工程的开始必须在另一些子工程完成之后。
2.拓扑排序的过程
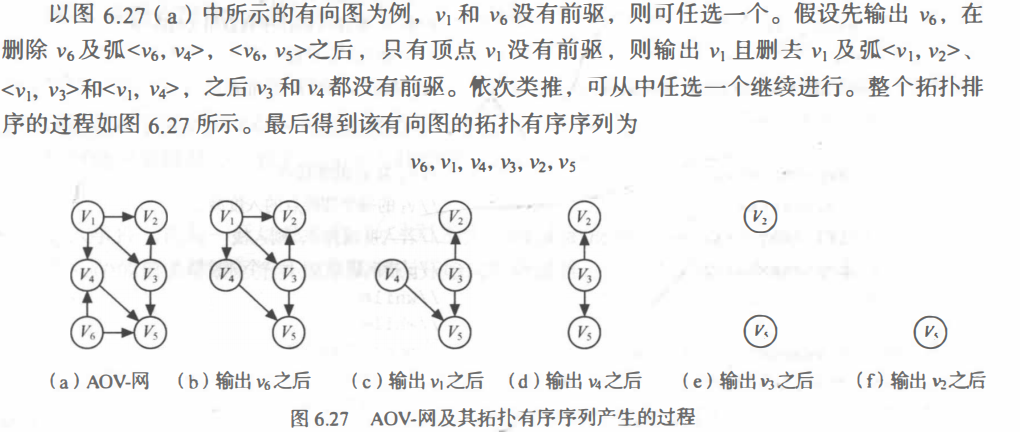
(1) 在有向图中选一个无前驱的顶点且输出它。
(2)从图中删除该顶点和所有以它为尾的弧。
(3) 重复 (1) 和 (2), 直至不存在无前驱的顶点。
(4)若此时输出的顶点数小千有向图中的顶点数,则说明有向图中存在环, 否则输出的顶点序列即为一个拓扑序列。
3.拓扑排序的实现
(1)一维数组 indegree[i]: 存放各顶点入度,没有前驱的顶点就是入度为零的顶点。 删除顶点及以它为尾的弧的操作,可不必真正对图的存储结构进行改变,可用弧头顶点的入度减l的办法来实现。
(2)栈S: 暂存所有入度为零的顶点,这样可以避免重复扫描数组indegree检测入度为0的顶点, 提高算法的效率。
(3)一维数组topo(i]: 记录拓扑序列的顶点序号。
算法6.12 拓扑排序
算法步骤
- 求出各顶点的入度存入数组 indegree[i]中, 并将入度为0 的顶点入栈。
- 只要栈不空, 则重复以下操作:
-
将栈顶顶点 vi出栈并保存在拓扑序列数组 topo 中;
-
对顶点 V;的每个邻接点 Vk的入度减1, 如果 Vk的入度变为0, 则将 Vk入栈。
3.如果输出顶点个数少于AOV-网的顶点个数, 则网中存在有向环, 无法进行拓扑排序, 否则拓扑排序成功。
算法描述
Status TopologicalSort(ALGraph G,int topo[])
{//有向图G采用邻接表存储结构
//若 G 无回路,则生成 G 的一个拓扑序列 topo []并返回 OK, 否则 ERROR
FindinDegree(G,indegree); //求出各顶点的入度存入数组 indegree中
InitStack(S)//栈 s初始化为空
for(i=O;i<G.vexnum;++i)
if (! indegree [i)) Push (S, i); //入度为0者进栈
m=O; //对输出顶点计数,初始为0
while (! StackEmpty (S)) //栈s非空
{
Pop (S, i); //将栈顶顶点Vi出栈
topo[m)=i; //将Vi保存在拓扑序列数组 topo中
++m; //对输出顶点计数
p=G.vertices[i) .firstarc; //p指向Vi的第一个邻接点
while (p!=NULL)
{
k=p->adjvex;//vk为 m 的邻接点
--indegree[k]; //vi的每个邻接点的入度减1
if(indegree[k)==O) Push(S,k); //若入度减为0, 则入栈
p=p->nextarc; //vi的每个邻接点的入度减1
}
}
if(m<G.vexnum) return ERROR; //该有向图有回路
else return OK;
}
6.6.4关键路径
1.AOE-网
与AOV-网相对应的是AOE-网 (Activity On Edge) , 即以边表示活动的网。 AOE-网是一个带权的有向无环图, 其中, 顶点表示事件, 弧表示活动, 权表示活动持续的时间。 通常, AOE-网可用来估算工程的完成时间。
2.关键路径求解的过程
(1)对图中顶点进行排序, 在排序过程中按拓扑序列求出每个事件的最早发生时间ve(i)。
( 2 )按逆拓扑序列求出每个事件的最迟发生时间vl(i)。
(3) 求出每个活动 a;的最早开始时间e(i)。
(4) 求出每个活动 a;的最晚开始时间l(i)-
( 5 )找出 e(i)= l(i)的活动a;, 即为关键活动。由关键活动形成的 由源点到汇点 的每一条路径就是关键路径, 关键路径有可能不止一条 。
3.关键路径算法的实现
算法步骤
算法描述
Status CriticalPath(ALGraph G)
{//G为邻接表存储的有向网,输出G的各项关键活动
if(!TopologicalOrder(G,topo)) return ERROR;
//调用拓扑排序算法,使拓扑序列保存在topo中,若调用失败, 则存在有向环, 返回ERROR
n=G. vexnum; //n为顶点个数
for(i=O;i<n; i++)//给每个事件的最早发生时间置初值0
/*- - - ----- -- - 按拓扑次序求每个事件的最早发生时间 - - - - - - ----*/
for (i=O; i<n; i++)
{
k=topo[i]; //取得拓扑序列中的顶点序号K
p=G.vertices[k].firstarc; //p指向k的第一个邻接顶点
while(p!=NULL);
{//依次更新k的所有邻接顶点的最早发生时间
j=p->adjvex;//j为邻接顶点的序号
if(ve[j]<ve[k]+p->weight)//更新顶点j的最早发生时间 ve[j]
ve[j]=ve[k]+p->weight;
p=p->nextarc;//p指向k的下一个邻接顶点
}
}
for(i=O;i<n;i++) //给每个事件的最迟发生时间置初值 ve[n-1]
vl[i]=ve[n-1];
/*-------------按逆拓扑次序求每个事件的最迟发生时间--- ----- ------*/
for(i=n-l;i>=O;i--)
{
k=topo[i];//取得拓扑序列中的顶点序号K
p=G.vertices[k) .firstarc;//p指向k的第一个邻接顶点
while(p!=NULL) //根据k的邻接点,更新k的最迟发生时间
{
j=p->adjvex; //j为邻接顶点的序号
if(vl[k]>vl[j)-p->weight) //更新顶点 K 的最迟发生时间 vl [k]
vl[k)=vl[j)-p->weight;
p=p->nextarc; //p指向k的下一个邻接顶点
}
}
/*---------- - - - -- -判断每一活动是否为关键活动-------*/
for(i=O;i<n;i++)//每次循环针对m为活动开始点的所有活动
{
p=G.vertices[i) .firsarc;//p指向1的第一个邻接项点
while (p ! =NULL)
{
j=p->adjvex; //j为i的邻接顶点的序号
e=ve[i]; //计算活动<Vi, Vj>的最早开始时间
l=vl[j)-p->weight; //计算活动<Vi, Vj>的最迟开始时间
if (e==l) //若为关键活动,则输出<vi, Vj>
cout<<G.vertices[i] .data <<G.vertices[j] .data;
p=p->nextarc; //p指向 i 的下一个邻接顶点
}
}
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号