10.18闲话
今天没模拟赛，爽爽爽🥰🥰🥰
上午看了看 nfls 的题，妈的 T1 怎么是大模拟啊😨😨😨，还是儒略日同等类型的大模拟，我儒略日还没写呢😭😭😭，于是摆了。去口胡 T2 口胡了俩小时没胡出来，上午感觉不能太摆，就去整理了整理板子，准备考完 csp 再打🤗🤗🤗。
后天就要去秦皇岛了！大后天就能开音趴了！现在开摆开摆开摆！！！🤤🤤🤤
感觉没有模拟赛的一天有点无趣捏😓，但是现在天天都能和初中组聊天，也是挺好的🤗。但是总感觉自己给初二的同学留下的印象不太好😨😨。反正他们不在我考试的时候在那吵就行😓😓😓，别的时候我可不管。
下午于是把儒略日看了看，发现确实不算太难写，只要想到二分就很好写了🤗🤗🤗。然后又看了看 csp 的 dp 题，发现自己一如既往的菜🤣🤣🤣。
昨天有人问断句相关，这里放下原版圣经，昨天那个是在这个基础上扩展的。
求你了别发了我音游打得再菜我都不会觉得难过只有你们发这种成绩图的时候我的心里像刀割一样地痛着打着字泪水就忍不住地往下流
最近又开始看音游区的抽象视频了，也想起来了经典圣经：
对一位非说话人和被说话人的男性使用的人称代词 五月第二个星期日中人们所感恩的对象 用在定语后名词前的助词，世界上最动听的语言 现代一种与电子产品密不可分的娱乐形式 在平面内到定点的距离等于定长的点的集合 对某个现象或某件事的原因进行发问的疑问词 事物不再是原先的状态 与“那”相对的指示代词 可用于修饰无专用量词的名词的量词 事物展现出的状态。
我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗我现在就要打Lost Emotion🥵😨😭🤗
感觉 arc 版本的 Lost Emotion 多了一些节奏，对于原版刻进 DNA 的有点不太适应，但是很适合音游就对了。
考完 csp 的晚上我要和庭哥睡一张床😍😍😍，我在他床上直接开始打交玩蛇😍😍😍
我闲话怎么全是在发电啊也没啥有意思的东西咋。
有个问题，这个图的作者是谁（）
推歌：［X］ -Blacklolita
搬运自 二多龙_
- 前言
这个应该挺典的，可能有人听说过。这个名字是我起的，可能不太恰当，但是说得高端一点比较吓人。反正是整活，叫 Top Tree 也行。
有看这篇文章的时间不如多写几道题（
- \(\text{mex}\) 反演能做什么
\(\text{mex}\) 反演提供了一种 \(O(n)-O(1)\) 求静态区间 \(\text{mex}\) 的算法。
- \(\text{mex}\) 反演是什么
从我们需要解决的静态区间 \(\text{mex}\) 问题引出该算法。
众所周知，使用四毛子算法，可以做到 \(O(n)-O(1)\) 求静态区间 \(\min\)。
显然，区间 \(\min\times\text{mex}\) 也是可以 \(O(1)\) 求出的，这一算法日益普及。
既然我们已经可以迅速求出区间 \(\min\) 以及区间 \(\min\times\text{mex}\)，有什么方法能将二者联系起来呢？人教版二年级小学数学课本给了我们启示。
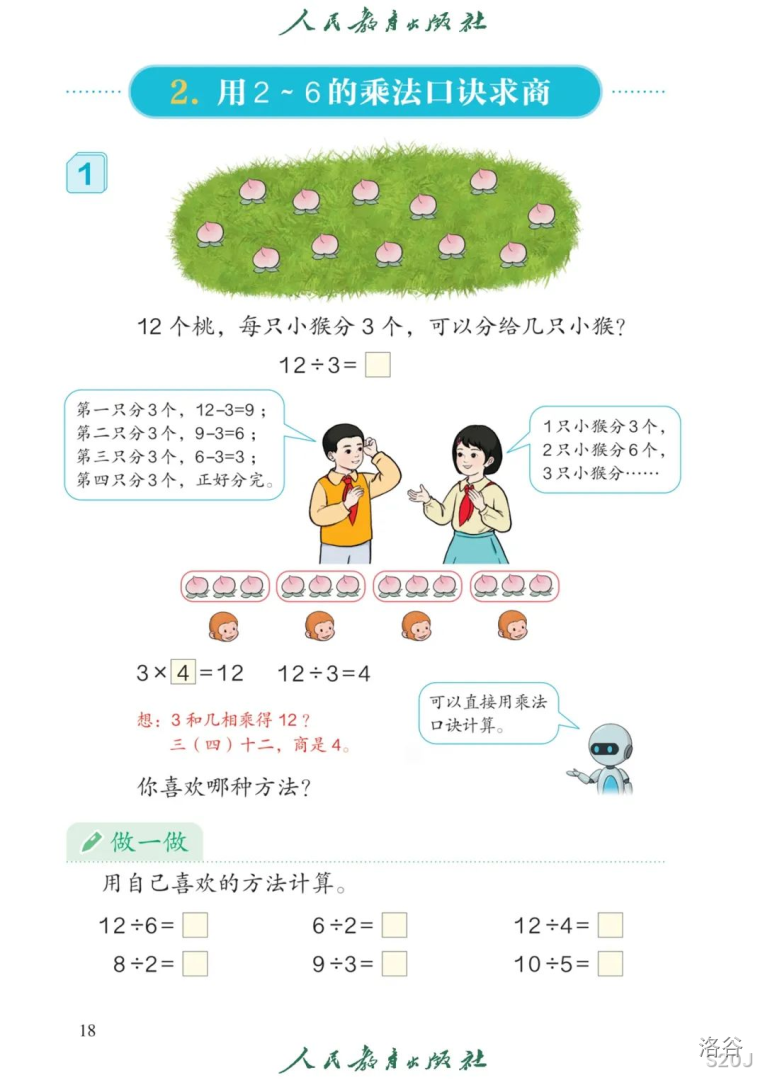
由此可见：
将 \(\min\) 代入 \(a\)，\(\text{mex}\) 代入 \(b\)，可得：
这一等式即为 \(\text{mex}\) 反演。
- 习题
给定长为 \(n\) 的自然数序列 \(a\) 和 \(q\) 次询问，每次询问给定 \(l,r\)，你需要求出
\(\text{mex}\{a_l,a_{l+1},\dots,a_{r-1},a_r\}\)。
- 输入格式
为了避免输入量过大，你只需读入一行四个整数 \(s,m,n,q\)，序列及询问将使用如下代码生成。
const int N=50000005;
unsigned s,m,n,q,a[N],l[N],r[N],t1,t2;
unsigned nrd(){return s^=s<<13,s^=s>>17,s^=s<<5,s;}
void geta(){a[++t1]=nrd()%m+1;}
void getq(){
++t2,l[t2]=nrd()%n+1,r[t2]=nrd()%n+1;
if(l[t2]>r[t2]) l[t2]^=r[t2]^=l[t2]^=r[t2];
}
void gen(){//shin
for(unsigned i=1;i<=n;++i) geta();
for(unsigned i=1;i<=q;++i) getq();
}
您需要在读取 \(s,m,n,q\) 后调用一次 gen 函数，然后对于 \(1\le i\le n\)， \(a_i\) 将被保存在 a[i] 中；对于 \(1\le i\le q\)，\(l_i\) 将被保存在 l[i] 中，\(r_i\) 将被保存在 r[i] 中。
- 输出格式
为了避免输出量过大，设第 \(i\) 次询问的答案为 \(b_i\)，你只需输出一个整数，表示对于 \(1\le i\le q\)，\(i\times b_i\) 的异或和。
- 数据范围
\(1\le s,m\le 10^9,1\le n,q\le 5\times 10^7\)。
标准程序
#include<cstdio>
int main(){return putchar(48),0;}
