9.18闲话

勿忘国耻。

今天返校了😓

早晨 5 点 50 起的，困死了。赶的火车来的，到机房已经 9 点了。因此模拟赛摆了。T1 火车上就切了。T2 火车上也切了。T3 不会，T4 看上去不太可做。只肝 T3 没干出来。最终 \(100+30+0+20=150pts\)，rk7。

上面都是赛时想法。下面是赛后：

什么几把逆天题目啊我草，这是我这辈子见过除了 9.15 那次比赛外最逆天的比赛之一了。T1 考 whk 是吧，我初三做了他妈一堆这题了，T2 造数据人不会造数据可以不造，连个区间不重叠都造不出来也真是难绷。T3 什么逆天 spj 啊，一个概率期望还带取模的用你妈的 spj，搬错 spj 了就直说。T4 没啥好说的，还行。

突然感觉去掉日常聊天逆天记录会不会不太好呢。

但是有好玩的东西时大概率也还是会分享出来吧。

最近虫子好多，原来潘队葡萄忘封口了😥😥😥，还是搞了搞卫生/qd

在家真舒服，昨天闲话忘写了，ptt+0.01 喽。AC 真好嫖 ptt🥰🥰🥰，但是被色号、蛋挞、绿魔王暴打了😨😨😨

在家还把洞、璋的 E 难度通了😋😋😋，舒服。

园神，琦洞！

东方兽王园 东方神灵庙 东方心绮楼 东方虹龙洞

---

有人能再推点歌吗啊啊啊

---

今天模拟赛 T3 题解捏。

我们先把问题转化为求所有序列的可以获得个数之和 \(ans\)，那么答案即为 \(\frac{ans}{A^n}\)。

我们考虑求出 \(ans\)。我们要求的是对于所有序列，它所能选的牌数之和。我们转化为对于所有牌数 \(d\)，选的牌数为 \(d\) 的序列乘上 \(d\) 之和。

设 \(g_{i, j, k}\) 为 \(i\) 个数，且这 \(i\) 个数都不超过 \(j\)，并且它们的和小于等于 \(k\) 的方案数。我们考虑我们把序列排序之后的样子：

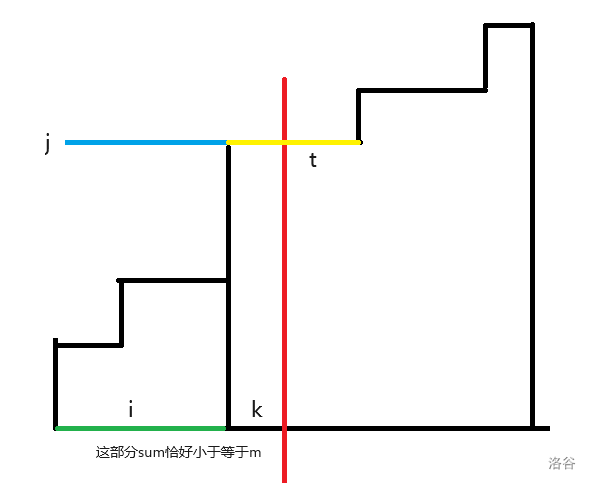
我们枚举图中的 \(i, j, k, t\)，然后再让它们插入到序列中，我们就能得到下面的式子：

\[ans=\sum_{i=0}^{n}\sum_{j=1}^A\sum_{k=1}^{n-i}g_{i, j-1, m-j\times k}\dbinom{n}{i}\sum_{t=k}^{n-i}\dbinom{n-i}{t}(A-j)^{n-t-i} \]

而这里没有乘以牌数的原因是因为：我们会在每一个放置新数的位置都对这个序列记一次数，也就达到了上面乘以牌数的效果。

而对于 \(g_{i, j, k}\) 的求法，我们可以用二项式反演来求：

简单地说，我们要求的简化版为下面这个式子：

\[x_1+x_2+\cdots +x_n=k\ \ x_i\le r \]

设 \(f_j\) 为恰好 \(j\) 个条件不满足，\(g_j\) 至少 \(j\) 个不满足，二项式反演可得：

\[f_i=\sum _{j=i}^n(-1)^{j-i}\dbinom{j}{i}g_j \]

先从 \(n\) 个限制选 \(j\) 个不满足，让这 \(j\) 个变为 \(x_i>r\)。然后再减去这 \(j\times r\)，变为 \(x_i>0\)。因为 \(x_i>0\)，所以直接变为 \(k-r\times j\) 个小球放 \(n\) 个盒子，盒子非空的模型：

\[g_j=\dbinom{n}{j}\dbinom{k-r\times j-1}{n-1} \]

因此 \(f_i=\sum _{j=i}^n(-1)^{j-i}\dbinom{j}{i}\dbinom{n}{j}\dbinom{k-r\times j-1}{n-1}\)，\(f_0=\sum _{j=0}^n(-1)^{j}\dbinom{n}{j}\dbinom{k-r\times j-1}{n-1}\)

而要求的 \(g_{n, r, x}\) 为和小于等于 \(x\) 的方案数，可以在前面再加个 \(\sum\)。

\[\begin{aligned} g_{n, r, x}&=\sum_{k=1}^{x}\sum _{j=0}^n(-1)^{j}\dbinom{n}{j}\dbinom{k-r\times j-1}{n-1}\\ &=\sum _{j=0}^n(-1)^{j}\dbinom{n}{j}\sum_{k=1}^{x}\dbinom{k-r\times j-1}{n-1}\\ &=\sum _{j=0}^n(-1)^{j}\dbinom{n}{j}\sum_{k=1-r\times j-1}^{x-r\times j-1}\dbinom{k}{n-1}\\ &=\sum _{j=i}^n(-1)^{j}\dbinom{n}{j}\sum_{k=0}^{x-r\times j-1}\dbinom{k}{n-1}\\ \end{aligned} \]

由于 \(\sum _{i=0}^n\dbinom{i}{m}=\dbinom{n+1}{m+1}\)，所以 \(g_{n, r, x}=\sum _{j=0}^n(-1)^{j}\dbinom{n}{j}\dbinom{x-r\times j}{n}\)。

这样我们就求出来了 \(g\)。

前面那一坨为 \(0\) 时可以跳过，那么复杂度可能是 \(O(n^2m\log m)\) 的，我也不会算。

我不知道我为什么要写这么详细（，可能我看到的绝大多数题解都说根据容斥就能算出这个 \(g\)，但是我总感觉一句容斥考场上用的时候真的会心慌/qd，所以我还是觉得二项式反演比较可依靠。

---

重要通知:近期接到举报，大量新生被诈骗网站https://toho-vote.info坑骗，如果误入请不要慌张，在人物投票界面给古明地恋投一票即可安全退出，请各位增强网络安全意识，避免上当受骗