感知机模型

模型概念

输入空间和输出空间

• \(\mathbf X \subseteq \mathbb R^n\)
• \(\mathbf Y = \{+1, -1\}\)
• \(\mathbf x \in \mathbf X\)
• \(y \in \mathbf Y\)

假设空间

\[f(\mathbf x) = sign(\mathbf w \cdot \mathbf x + b) \]

\(w\)和\(b\)是感知机的模型参数，\(\mathbf w \subseteq \mathbb R^n\)叫做权重向量，\(b \in \mathbb R\)叫做偏置。\(\mathbf w \cdot \mathbf x\)表示\(w\)和\(x\)的内积，\(sign\)是符号函数，即

\[sign(x) =\begin{cases} +1& x \geq 0 \\ -1& x < 0 \end{cases} \]

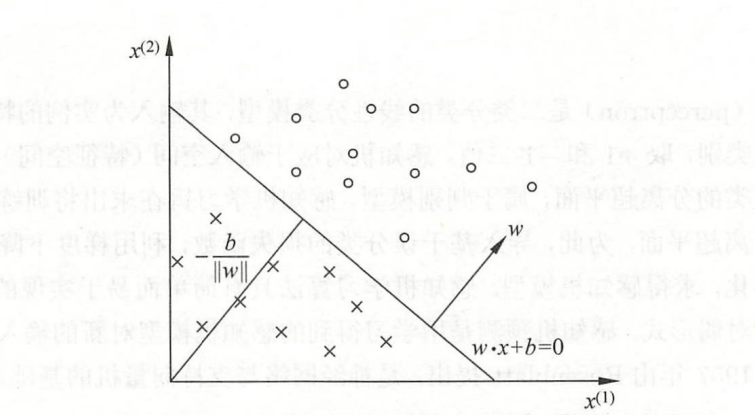
学习策略

点\(\mathbf x_0\)到直线\(y = \mathbf w \cdot \mathbf x + b\)的距离

\[distance = \frac{1}{||\mathbf w||}|\mathbf w \cdot \mathbf x_0 + b| \]

对于误分类点\((x_i,y_i)\)，如果\(\mathbf w \cdot \mathbf x_i + b < 0\)，那么\(y_i= +1\)；反之，如果\(\mathbf w \cdot \mathbf x_i + b > 0\)，那么\(y_i=-1\)。所以，将距离公式去掉绝对值，误分类点到超平面的距离可以表示为

\[-\frac{1}{||\mathbf w||}y_i(\mathbf w \cdot \mathbf x_i + b) \]

损失函数的定义：误分类点到超平面的总距离

\[L(\mathbf w,b) = - \sum_{x_i \in M} \frac{1}{||\mathbf w||}y_i(\mathbf w \cdot \mathbf x_i + b) \]

其中\(M\)为误分类点的集合

对于感知机算法使用梯度下降法求解

\[\frac{\partial L}{\partial \mathbf w} = - \sum_{x_i \in M}y_ix_i\\ \frac{\partial L}{\partial b} = - \sum_{x_i \in M}y_i \]

在训练过程中，使用随机梯度下降法，随机选取一个误分类点，对\(w\)，\(b\)更新

\[\mathbf w = \mathbf w + \eta y_ix_i\\ b = b + \eta y_y \]

问题：为什么参数更新的时候不需要考虑\(\frac{1}{||w||}\)?

分离超平面通过\(w\)和\(b\)确定，\(\frac{1}{||w||}\)对\(w\)的方向没有影响，可以固定\(w\)的大小为1。

从上述学习过程中可以看出来，假如\(w\)和\(b\)的初始值都设为\(0\)，\(\eta\)的初始值设为\(1\)，那么\(w\)在误分类点\((x_i,y_i)\)的驱动下的增量为\(y_ix_i\)，\(b\)的增量为\(y_i\)。设误分类点\((x_i,y_i)\)对\(w\)和\(b\)的修正次数为\(a_i\),那么最终\(w=\sum_{i=1}^{N}a_iy_ix_i\)，\(b = \sum_{i=1}^{N}a_iy_i\)。

此时的模型可以表示为

\[f(\mathbf x) = sign(\sum_{j=1}^{N}a_jy_jx_j \cdot x + b) \]

算法

感知机学习算法的原始形式

class Perceptron:
    def __init__(self, alpha=0.1):
        self.alpha = alpha
        self.w = None
        self.b = None

    def fit(self, X, y):
        self.w = np.ones_like(X[0])
        self.b = 0.0
        flag = 1
        while flag:
            flag = 0
            for xi, yi in zip(X, y):
                if yi * (np.dot(self.w, xi) + self.b) <= 0:
                    self.w += self.alpha * yi * xi
                    self.b += self.alpha * yi
                    flag = 1

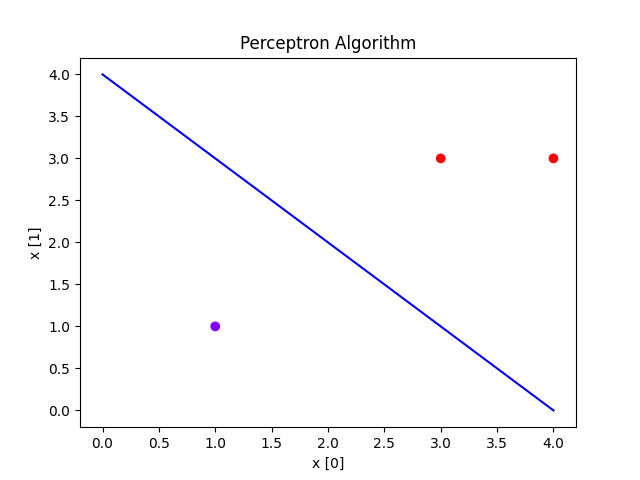
可视化结果

def plot(X, y, model):
    w = model.w
    b = model.b
    print(w, b)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow')
    plt.plot(range(5), [-w[0] / w[1] * x - model.b / w[0] for x in range(5)], c="b")
    plt.xlabel("x [0]")
    plt.ylabel("x [1]")
    plt.title("Perceptron Algorithm")
    plt.show()


def main():
    model = Perceptron(alpha=1)
    X = np.array([[3., 3.], [4., 3.], [1., 1.]])
    y = np.array([1., 1., -1.])
    model.fit(X, y)
    plot(X, y, model)

感知机学习算法的对偶形式

class Perceptron:
    def __init__(self, alpha=0.1):
        self.alpha = alpha
        self.a = None
        self.b = None

    def fit(self, X, y):
        self.a = np.zeros(X.shape[0])
        self.b = 0.0
        flag = 1
        while flag:
            flag = 0
            for i, (xi, yi) in enumerate(zip(X, y)):
                if yi * (sum([self.a[j] * y[j] * np.dot(x, xi) for j, x in enumerate(X)]) + self.b) <= 0:
                    self.a[i] += self.alpha
                    self.b += self.alpha * yi
                    flag = 1

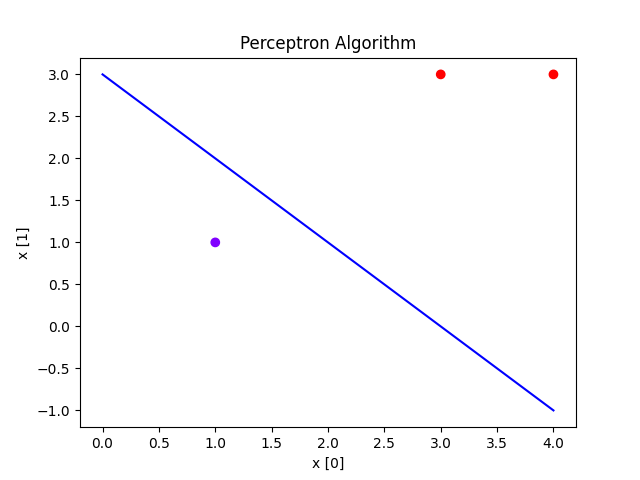
可视化结果

def plot(X, y, model):
    w = np.sum(np.array([model.a[i] * y[i] * x for i, x in enumerate(X)]), axis=0)
    b = np.sum(np.array([model.a[i] * y[i] for i, x in enumerate(X)]), axis=0)
    print(w, b)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow')
    plt.plot(range(5), [-w[0] / w[1] * x - model.b / w[0] for x in range(5)], c="b")
    plt.xlabel("x [0]")
    plt.ylabel("x [1]")
    plt.title("Perceptron Algorithm")
    plt.show()


def main():
    model = Perceptron(alpha=1)
    X = np.array([[3., 3.], [4., 3.], [1., 1.]])
    y = np.array([1., 1., -1.])
    model.fit(X, y)
    plot(X, y, model)

算法的收敛性

详细证明过程参照李航老师《统计学习方法》

算法的收敛性证明表明，在数据集线性可分的情况下，搜索次数\(k\)是有上界的，经过有限次搜索可以找到将训练数据完全正确分开的超平面。