模型评估与选择

混淆矩阵#

对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为真正例($true$ $positive$) 、假正例 ($false$ $positive$) 、真反例($true$ $negative$) 假反例 ($false$ $negative$) 四种情形，用$TP、FP、TN、FN$分别表示其对应的样例数。

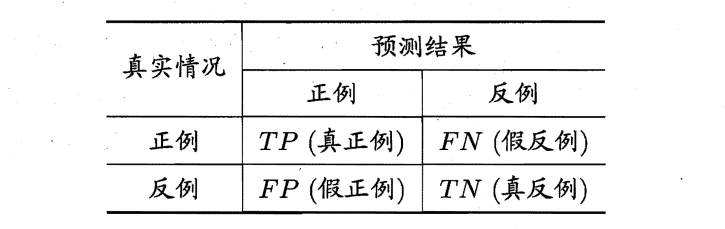
查全率、查准率和$F1$#

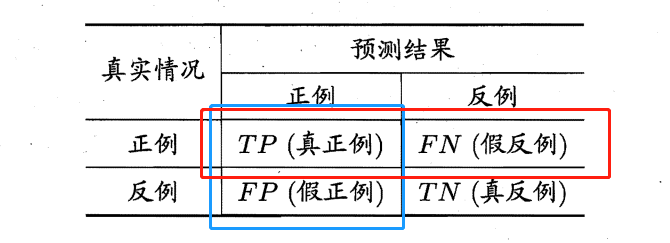
查全率

红框中$TP$的比例

$$R = \frac{TP}{TP+FN}$$

查准率

蓝框中$TP$的比例

$$P = \frac{TP}{TP + FP}$$

查准率和查全率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

例如，若希望将好瓜尽可能多地选出来， 则可通过增加选瓜的数量来实现，如果将所有西瓜都选上，那么所有的好瓜也必然都被选上了，但这样查准率就会较低；若希望选的瓜中好瓜比例尽可能高，则可只挑选最有把握的瓜 但这样就难免会漏掉不少好瓜，使得查全率较低。

$F1$​

$F1$值综合考虑查准率和查全率的性能

$$F1 = \frac{2 \times P \times R}{P + R}$$

$PR$曲线#

根据学习器的预测结果对样例进行排序，排在前面的是学习器认为"最可能 "是正例的样本，排在最后的则是学习器认为"最不可能"是正例的样本。按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、 查准率。以信息检索应用为例，逐条向用户反馈其可能感兴趣的信息，即可计算出查全率、查准率。

以查准率为纵轴、查全率为横轴作图 ，就得到了查准率查全率曲线，亦称$PR$曲线或$PR$图。

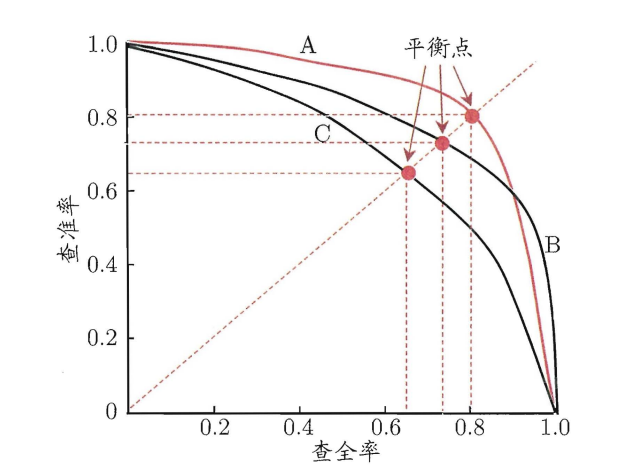
PR 曲线直观地显示出学习器在样本总体上的查全率、 查准率。在进行比较时，若一个学习器的 PR 曲线被另一个学习器的曲线完全"包住，则可断言后者的性能优于前者。如图，学习器$A$的性能优学习器$C$。

如果两个学习器$PR$曲线发生了交叉，例如图中的$A$与$B$ ，则难以一般性地断言两者孰优孰劣，只能在具体的查准率或查全率条件下进行比较。然而，在很多情形下，人们往往仍希望把学习器比出个高低，这时一个比较合理的判据是比较$PR$曲积的大小，它在一定程度上表征了学习器在查准率和查全率上取得相对"双高"的比例，但这个值不太容易估算， 因此人们设计了一些综合考虑查准和查全率的性能度量。

"平衡点“($Break-Event Point $，简称$BEP$)就是这样一个度量，它是" 查准率=查全率"时的取值。基于$BEP$的比较，可认为学习器$A$优于$B$。

$ROC$和$AUC$#

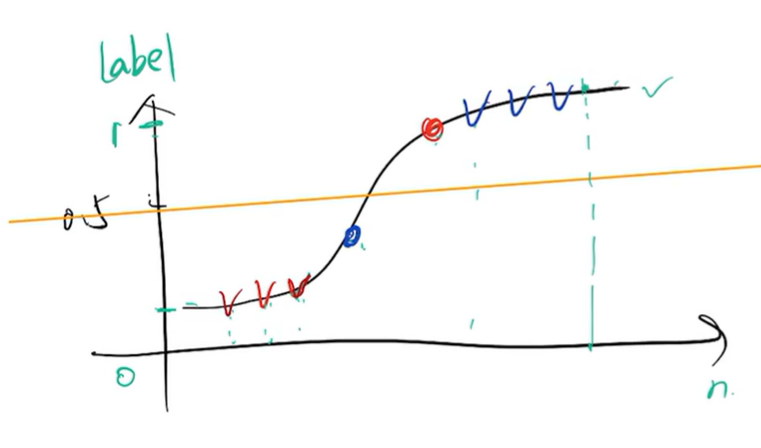
很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阔值($threshold$) 进行比较，若大于阈值则分为正类，否则为反类。

如图所示，阈值选为0.5，则TP=3、FP=1、FN=1、TN=3。当阈值发生变化时，在每一个阈值下都会对应一个混淆矩阵。

$TPR$

真阳性率

$$TPR = \frac{TP}{TP + FN}$$

$FPR$

假阳性率

$$FPR = \frac{FP}{FP + TN}$$

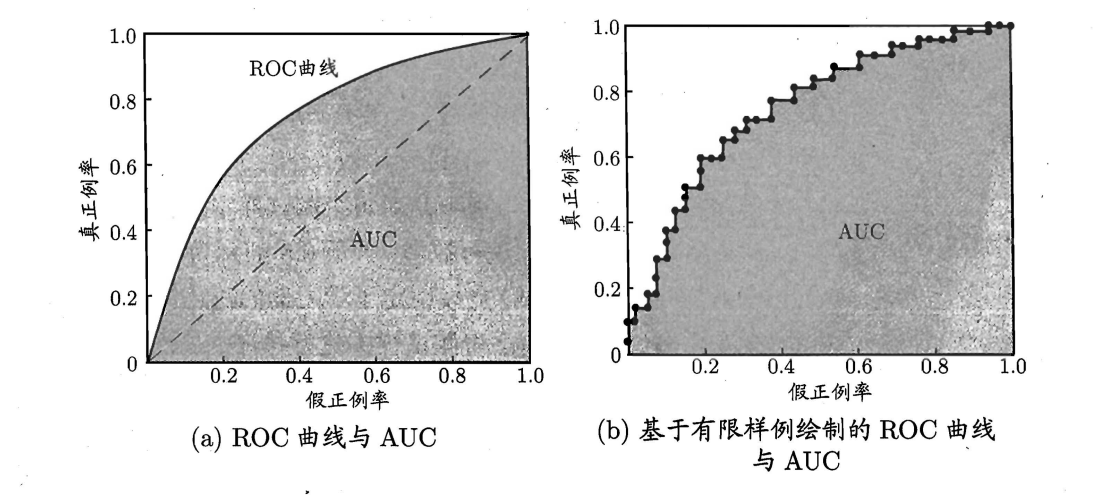
$ROC$($Receiver$ $Operating$ $Characteristic$)：我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出$TPR$和$FPR$的值，以$TPR$为纵轴，以$FPR$为横轴作图就得到了$ROC$曲线。

$AUC$($Area$ $Under$ $ROC$ $Curve$) ：一个学习器的$ROC$曲线被另学习器的曲线完全"包住"，则可断言后者的性能优于前者；若两个学习器$ROC$曲线发生交叉，则难以一般性地断言两者孰优孰，此时如果一定要进行比较则较为合理的判据是比较$ROC$线下的面积$AUC$。