数据结构与算法(周鹏-未出版)-第六章 树-6.1 树的定义及基本术语

第六章 树

目录

6.1 树的定义及基本术语

6.2 二叉树

6.3 二叉树基本操作的实现

6.4 树、森林

6.5 Huffman 树

 

前面我们介绍了线性表、栈和队列，这些数据结构都是线性结构，在本章中我们介绍一种重要的非线性结构——树。在第二章曾经介绍，在树结构中数据元素之间的逻辑关系是前驱唯一而后续不唯一，即数据元素之间是一对多的关系。如果直观的观察，树结构是具有分支的层次结构。树结构在客观世界中广泛存在，如行政区划、社会组织机构、家族世系等都

可以抽象为树结构。树结构在计算机科学领域也有非常广泛的应用，例如文件系统、编译系统、数据库系统、域名系统等领域。

本章重点讨论二叉树的存储表示及其各种运算，并研究一般树和森林与二叉树的转换关系，最后介绍树的应用实例。从本章开始逐渐将注意力转向算法，对于抽象数据类型的完整封装实现可以通过本书提供的源代码获得。

 

6.1 树的定义及基本术语

树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或简称为树根。我们可以形式地给出树的递归定义如下：

 

树（ tree） 是 n（ n ≥ 0）个结点的有限集。它

1) 或者是一棵空树（ n = 0），空树中不包含任何结点。

2) 或者是一棵非空树（ n > 0），此时有且仅有一个特定的称为根（ root） 的结点；

当n > 1 时，其余结点可分为m（ m > 0）个互不相交的有限集T1， T2， …， Tm，

其中每一个本身又是一棵树，并且称为根的子树（ sub tree）。

 

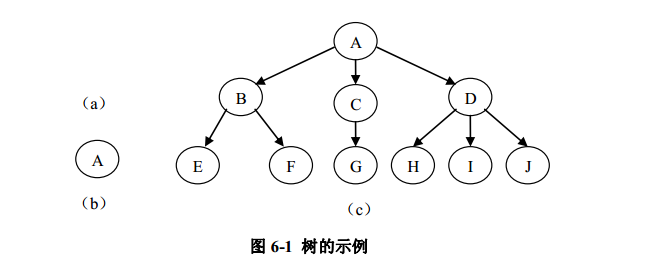
例如图 6-1（ a）是一棵空树、 6-1 （ b）是只有一个根节点的树、 6-1 （ c）是一棵有 10个结点的树，其中 A是根，其余的结点分成 3 个不相交的集合： T1={B,E,F} 、 T2={C,G} 、T3={D,H,I,J}，每个集合都构成一棵树，且都是根A的子树。例如T1是一棵树，其中B是根，其余结点构成 2 个不相交的集合： T11={E}、 T12={F}是B的子树，并且都是只有一个根结点

的树。

 

下面给出树结构中的一些基本术语：

 

1.@结点的层次和树的深度

树的结点包含一个数据元素及若干指向其子树的若干分支。结点的层次（ level） 从根开始定义，层次数为 0 的结点是根结点，其子树的根的层次数为 1。若结点在 L 层，其子树的根就在 L+1 层。对于层次为 k（ k > 0）的每个结点 c，都有且仅有一个层次为 k-1 的结点 p与之对应， p 称为 c 的父亲（ parent） 或父结点。若 p 是 c 的父亲，则 c 称为 p 的孩子（ child）。

父子之间的连线是树的一条边。在树中根结点没有父亲，其余结点只有一个父结点，但是却

可能有多个孩子，同一结点的孩子相互称为兄弟（ sibling）。

树中结点的最大层次数称为树的深度（ Depth） 或高度。树中结点也有高度，其高度是

以该结点为根的树的高度。

 

例如，在图 6-1（ c）中，结点 A 在第 0 层，结点 B、 C、 D 在第 1 层，结点 E、 F、 G、H、 I、 J 在第 2 层。结点 A 是结点 B、 C、 D 的父亲，结点 B、 C、 D 是结点 A 的孩子。由于结点 H、 I、 J 有同一个父结点 D，因此它们互为兄弟。以 A 为根的树的高度为 2，结点 A 的高度也就为 2。

 

2.@结点的度与树的度

 

结点拥有的子树的数目称为结点的度（ Degree）。度为 0 的结点称为叶子（ leaf） 或终

端结点。度不为 0 的结点称为非终端结点或分支结点。除根之外的分支结点也称为内部结点。

在这里需要注意的是结点的直接前驱结点，即它的父结点不计入其度数。

 

例如，在图 6-1（ c）中，结点 A、 D 的度为 3，结点 E、 F、 G、 H、 I、 J 的度均为 0，是叶子。

 

3.@在树结构中有一个重要的性质如下：

 

性质 6.1 树中的结点数等于树的边数加 1，也等于所有结点的度数之和加 1。

 

这是因为除根结点以外每个结点都与指向它的一条边对应，所以除根结点以外的结点数等于树中边数之和。因此树中的结点数等于树的边数加 1。而边数之和就是所有结点的度数之和，因此树中的结点数也等于所有结点的度数之和加 1。

 

性质 6.1 说明在树中结点总数与边的总数是相当的，基于这一事实，在对涉及树结构的算法复杂性进行分析时，可以用结点的数目作为规模的度量。

 

4.@路径

在树中k+1 个结点通过k条边连接构成的序列{（ v0,v1） ,（ v1,v2） , … ,（ vk-1,vk） | k ≥ 0}，称为长度为k的路径（ path）。注意，此时忽略了树中边的方向。由单个结点， 0 条边构成的是长度为 0 的路径。

 

例如，在图 6-1（ c）中， {（ F,B） ,（ B,A） , （ A,C） ,（ C,G） }构成了一条连接结点 F、G 长度为 4 的路径。

 

通过观察，不难得到如下观察结论：树中任意两个结点之间都存在唯一的路径。这意味着树既是连通的，同时又不会出现环路。从根结点开始，存在到其他任意结点的一条唯一路径，根到某个结点路径的长度，恰好是该结点的层次数。

 

5.@祖先、子孙、堂兄弟

 

将父子关系进行扩展，就可以得到祖先、子孙、堂兄弟等关系。结点的祖先是从根到该结点路径上的所有结点。以某结点为根的树中的任一结点都称为该结点的子孙。父亲在同一层次的结点互为堂兄弟。

例如，在图 6-1（ c）中，结点 H 的祖先为结点 A、 D。结点 B 的子孙有结点 E、 F。结点 E、 F 与结点 G、 H、 I、 J 互为堂兄弟。

 

6.@有序树、m 叉树、森林

如果将树中结点的各子树看成是从左至右是有次序的，则称该树为有序树；若不考虑子

树的顺序则称为无序树。对于有序树，我们可以明确的定义每个结点的第一个孩子、第二个

孩子等，直到最后一个孩子。若不特别指明，一般讨论的树都是有序树。

 

树中所有结点最大度数为 m 的有序树称为 m 叉树。

 

森林（ forest） 是 m（ m ≥ 0 ）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。树和森林的概念相近。删去一棵树的根，就得到一个森林；反之，加上一个结点作树根，森林就变为一棵树。例如，在图 6-1（ c）中，以结点 A 为根的树就是一棵 3 叉树。结点 A 的所有子树可以

组成一个森林。

 

下面给出树的抽象数据类型的定义。

ADT Tree{

数据对象 D： D 是具有相同性质的数据元素的集合。

数据关系 R： 若 D=Φ 则 R =Φ； 若 D≠Φ，则 R = {H}， H 是如下二元关系：

① 在 D 中存在一个唯一的称为根的元素 root，它在 H 下无前驱；

② 除 root 以外， D 中每个结点在 H 下都有且仅有一个前驱。

 

基本操作：

 

 

}ADT Tree

 

 

---