神经网络

模型表示

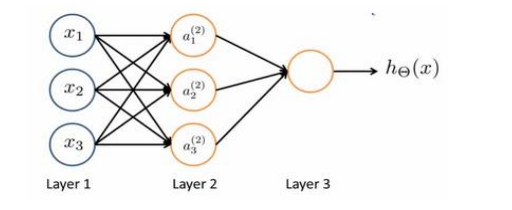
如上图，x123作为输入单元（input units),传入原始数据

a123是中间单元，处理数据并传递到下一层

最后为输出单元，负责计算\(h_\theta(x)\)

神经网络模型由许多逻辑单元按照不同层级组织起来的网络，每一层都是下一层的输入变量如图第一层为输入层

最后一层是输出层，中间的为隐藏层，为每一层增加一个偏差单位（bias unit）

以上，\(a_i^{(j)}\)是第j层的第i个激活单元。\(\theta^{(j)}\) 表示从j层到j+1层的权重的矩阵，例如\(\theta^{(1)}\)代表1到2层的权重的矩阵，尺寸为：以j+1层的激活单元数量为行数，j层的激活单元为列数的矩阵，上图中的第1层的权重的矩阵就为3*4（输入层还包含x0未显示）

又如图，激活单元和输出的表达分别如下

\(\alpha_1^{(2)} = g(\theta_{10}^{(1)}x_0 + \theta_{11}^{(1)}x_1 + \theta_{12}^{(1)}x_2 + \theta_{13}^{(1)}x_3)\)

\(\alpha_2^{(2)} = g(\theta_{20}^{(1)}x_0 + \theta_{21}^{(1)}x_1 + \theta_{22}^{(1)}x_2 + \theta_{23}^{(1)}x_3)\)

\(\alpha_3^{(2)} = g(\theta_{30}^{(1)}x_0 + \theta_{31}^{(1)}x_1 + \theta_{32}^{(1)}x_2 + \theta_{33}^{(1)}x_3)\)

\(h_\theta(x) = g(\theta_{10}^{(2)}a_0^{(2)}+\theta_{11}^{(2)}a_1^{(2)}+\theta_{12}^{(2)}a_2^{(2)}+\theta_{13}^{(2)}a_3^{(2)})\)

上述表达只是将一个训练实例送入神经网络中， 我们要做的是将整个训练集都送入神经网络算法来训练模型

实际展开来看就是

\(x = \begin{bmatrix} x_0\\x_1 \\x_2 \\ x_3\end{bmatrix}\) \(z^{(2)} = \begin{bmatrix}z_1^{(2)} \\z_2^{(2)}\\z_3^{(2)} \end{bmatrix}\)

\(z^{(2)} = \theta^{(1)}x \\a^{(2)} = g(z^{(2)})\)

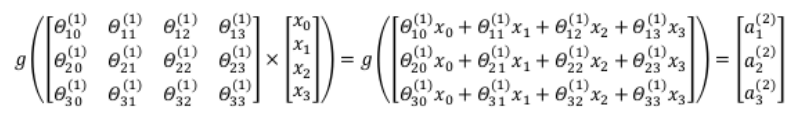
\(z^{(2) } = \theta^{(1)}x\) 即第二层的神经元数据为\(a^{(2)} = g(z^{(2)})\) ,得到第二层向量之后，添加偏移量\(a_0^{(2)}=1\),输入到下一层中，不妨假设下一层即为输出层，得到的就是

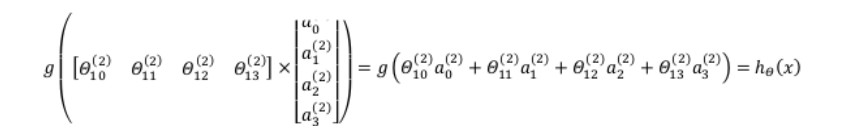
使\(z^{(3)} = \theta^{(2)}a^{(2)} 即h_\theta(x) = a^{(3)} = g(z^{(3)})\)

相对于逻辑回归和线性回归，神经网络经过了输入层和隐藏层的多此进化，可以简单的将中间的隐藏层看作原始输入数据的进化体，因为是由初始的x向量决定的，所以是梯度下降的，相比起来也下降的更加快速，所以中间的隐藏层特征值的效果也比x次方更加高效。

特征和直观理解

神经网络中单层神经元（无中间层）的计算可以用来表示逻辑运算例如逻辑与/或

举例说明

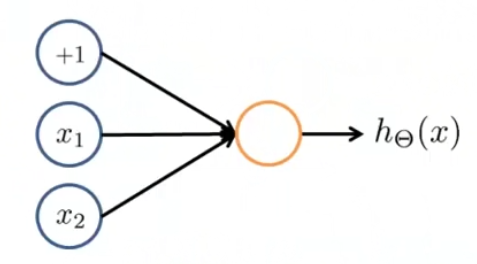
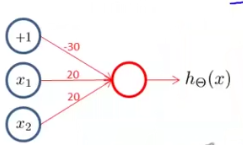
对于上图，我们首先需要在x12的基础上添加一个偏执单元，并为其分配一定的权重，例如-30，20，20，意味着x012的权重依次为上述三个值，我们可以得到\(h_{\theta}(x) = g(-30+20x_1+20x_2)\)

对于sigmoid函数 是一个x轴上从-∞到+∞，y值从0->1的激活函数图像，所以，对于h(x)有

即说明\(h_{\theta}(x) = x_1\quad AND\quad x_2\)

样本和直观理解

我们尝试使用神经元来组件神经网络实现运算功能，以下以异或功能为例

XNOR = \((x_1 \ and \ x_2) \ or \ ((not \ x_1) \ and \ (not \ x_2))\)

所以第一步我们需要构建表达\((not \ x_1) \ and \ (not \ x_2)\)的神经元\(g(10*1+-20*x_1+-20*x_2)\)

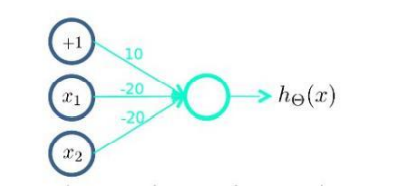
再表示出\((x_1 \ and \ x_2)\) \(g(-30 + 20 x_1 + 20 x_2)\)

将以上两个神经元并列后得到第二层神经元(hidden layer)，并得到最后的输出假设函数h(x)

由数据表示可以设计为

其中 \(a_1^{(2)} 神经元为和运算，a_2^{(2)}神经元为\)\((not \ x_1) \ and \ (not \ x_2)\)运算

\(x_1\)	\(x_2\)	\(a_1^{(2)}\)	\(a_2^{(2)}\)	\(h_\theta(x)\)
0	0	0	1	1
0	1	0	0	0
1	0	0	0	0
1	1	1	0	1

由上可得一个由一层输入一层隐藏层的神经网络，实现异或的功能

这样的方式可以构造出非常复杂的神经网络，可以挖掘到更加细致的特征值，这就是神经网络的优势所在

多类分类

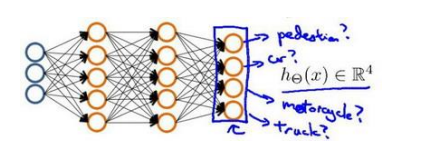
通常情况下，我们会遇到不止两种分类的问题，例如我们使用神经网络算法来识别四类图片，并输出一个四维向量来实现，例如[a,b,c,d],abcd中的任意一个为1，其余三个为0，表示图片为值为1的那类。对于神经网络的结构，可能如下图