正则化

过拟合

在建立模型的过程中，可能因为特征过多等问题出现过拟合

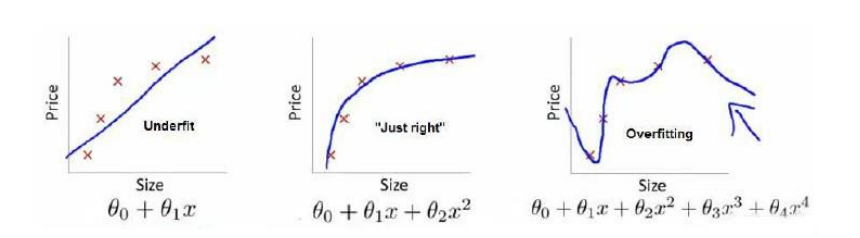
如上图在回归问题上，左图欠拟合，右图为过拟合， 中间的模型拟合效果最佳

又如下图的分类问题上存在同样的问题

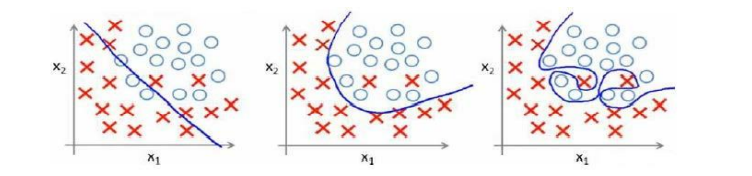
对此我们可以理解为，以多项式为模型基础的情况，变量次数越高，个数越多，拟合程度越好，但是更容易过拟合，影响预测的效果

改进建议

1、舍弃部分不重要的特征值，手工选择或借助模型选择的算法（如PCA）

2、正则化。保留所有的特征值但是修改参数的权重（原视频为大小，个人认为理解为权重合理些）。

代价函数

以回归为例，在模型\(h_\theta(x)= \theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+\theta_4x_4^4\)

是因为高次项导致了过拟合的出现，所以需要力求降低高次项对拟合过程的影响，正则化要做的就是努力减小高次项对模型整体的影响因子，对高次项的参数进行惩罚例如修改模型如下

\({min}_\theta \frac{1}{2m}[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2+1000 \theta^2_3+10000\theta_4^2]\)

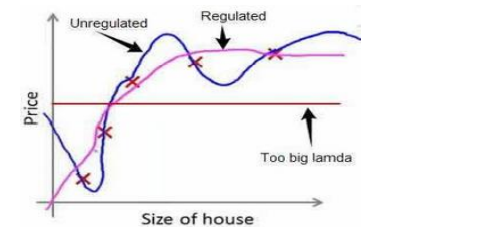
如上采取惩罚措施之后的得到了比原来更好的拟合效果，采用这样的思路，我们可以得出一个防止因为高次项导致的过拟合的假设模型

\(J(\theta) = \frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)})^2 + \lambda\sum^n_{j=1}\theta^2_j]\)

对于上述假设，我们称\(\lambda\) 为正则化参数，如果出现\(\lambda\) 过大，则会导致所有\(\theta\)值减小，导致\(h_\theta(x)=\theta_0\),出现欠拟合情况

正则化线性回归

此时我们要使用梯队下降使得这个代价函数最小化，在未实现正则化的前提下，梯度下降有以下两种情况

\(\theta_0 = \theta_0 - \alpha \frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}\)

\(\theta_j = \theta_j - \alpha [\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j\)

调整j=123.n可得

\(\theta_j = \theta_j(1-\alpha \frac{\lambda}{m} )-\alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}\)

可以看出正则化实际上是在原有更新的基础上让\(\theta\)值减少了一些

正则化逻辑回归

给代价函数增加一个正则化表达式，适用于逻辑回归，得到代价函数如下

\(J(\theta) = \frac{1}{m} \sum^m_{i=1}[-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum^n_{j=1}\theta_j^2\)

求导可得梯度下降算法为

\(\theta_0 = \theta_0 - \alpha \frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}\)

\(\theta_j = \theta_j - \alpha [\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j\)

形式上和线性回归相同，但是实际上\(h_\theta(x) = g(\theta^TX)\),(g函数可能为sigmoid等和函数)，所以实质上不同

注意：

1、正则化的逻辑回归的梯度下降和正则化的线性回归只是表达式相同，但是两者的h(x)假设完全不同

2、\(\theta_0\)并不参与正则化，即便是直接使用标准方程计算，后面的\(\theta_0\)在矩阵中也需要设置为0