逻辑回归(logistic Regression)

分类问题

在分类中，如果要预测的变量y的离散的，我们将这一学习过程称之为逻辑回归，可以判断的二元以至多元问题

二元分类

两个类分别为正向、负向类，因变量y={0，1}，0为负向类，1为正向类，预测过程中，我们设置一个阈值，例如$h(\theta) > 0.5 \ y=1 \ \\h(\theta)<=0.5 \ y=0$

对于逻辑回归算法，我们要做到的是，将输出值控制在0-1之间

假说表示

要实现因变量y的值在0-1之间， 我们要引入逻辑回归模型，回归模型的假设是 $h_\theta(x) \;=\; g(\theta^TX)$

X为特征向量，g表示的是逻辑函数，假设中$\theta^TX$即为求得的y，经过g逻辑函数变换之后得到0-1之间的值

常用的g函数有sigmoid函数 $g(z) = \frac{1}{1+e^{-z}}$

$h_\theta(x)$的作用就是给出输入变量为正向类的几率，比如$h_\theta(x) = 0.7$表明有70%的几率使y为正向类（y=1），那么

P(y=0|x;$\theta$) = 1 - $h_\theta(x)$ = 0.3

判断边界

逻辑回归时

当$h_\theta(x)>=0.5$，也就是$g(\theta^TX)>=0.5$ 预测y = 1

当$h_\theta(x)<0.5$，也就是$g(\theta^TX)<0.5$预测y = 0

反映在坐标轴上就是（x轴表示正负向）

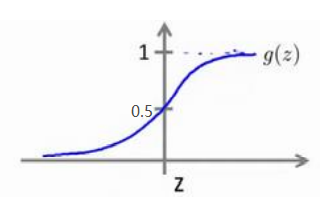
代价函数

对于线性回归模型的损失(代价)函数，使用的是所有实例（模型）的误差的平方和，代价函数是光滑的如下图

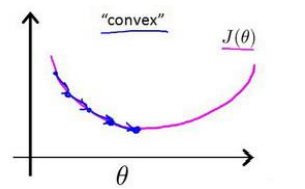
但是对于例如逻辑回归模型中用的$h_\theta(x) = \frac{1}{1+e^{-\theta^TX}}$是非线性的，表现在坐标轴上是一个非凸函数，例如下图

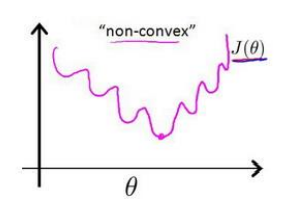
也就意味着损失（代价）函数存在很多的局部最优解（极小值），会影响梯度下降算法寻找最小值

面对这种情况我们要做的是找到一种损失（代价）函数的构造方法使得其为凸函数（convex），

损失函数$J(\theta) = \frac{1}{m} \sum^m_{i=1}Cost(h_\theta(x^{(i)}),y^{(i)})$

其中$Cost(h_\theta(x),y) = \left\{ \begin{aligned} -log(h_\theta(x)) \quad if \ y = 1 \\-log(1-h_\theta(x)) \quad if \ y = 0\end{aligned} \right.$

上述损失函数的图像如下

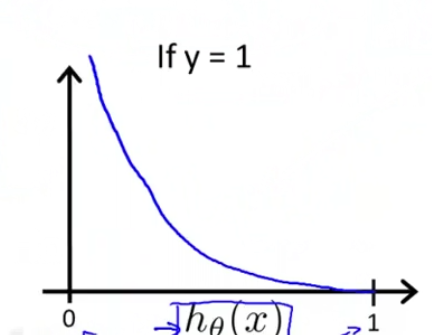
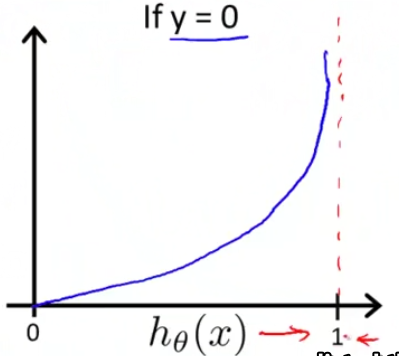
当y=1的时候，如果预测值h=0，那么损失函数肯定趋于无穷大，反之y=0，预测值=1同理

简化的成本函数和梯度下降

以上损失函数公式可以化简为

$Cost(h_\theta(x),y) = -y*log(h_\theta(x))-(1-y)*log(1-h_\theta(x))$

代价函数也就是$J(\theta) = \frac{1}{m} \sum_{i=1}^mCost(H_\theta(x),y)$

有上面这样一个代价函数之后，我们就可以使用梯度下降

$\theta_j = \theta_j - \alpha \frac{\partial}{ \partial \theta_j}J(\theta)$

也就是 $\theta_j = \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$

上述式子需要注意的是，逻辑回归的预测值函数与线性回归的不同，使用的是sigmoid函数，而不是直接计算$\theta^TX$，所以与线性回归并不相同

高级优化

与梯度下降不同，我们也有一些更高级、复杂的算法，类似共轭梯度法BFGS，L-BFGS（限制变尺度法）

以上几种高级方法的有点是，不需要手动设置 $\alpha$值且往往比梯度下降法更加快速，但是更加复杂

多类别分类：一对多

简单的举例：要将病人当前的状态分类，y=0表示没生病 y=1表示感冒，y=2表示流感

相当于有三块聚集的类别且各不相同，这种一对多的分类问题又被称之为一对余的方法，也就是先选定一个类别作为正向类1，其余的类别相当于反向类0，如下图所示

。

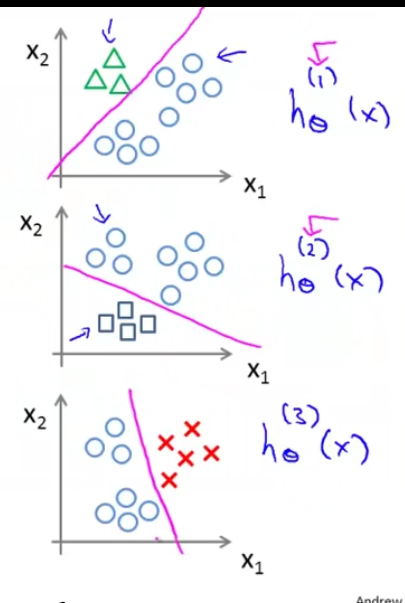
也就相当于我们得到了三个分类器分别将这类1，2，3分为 类1&&其他，类2&&其他，类3&&其他

记录为$h^{(i)}_\theta(x)$ ,其中类i为正向类，其余为负向类， 且$h^{(i)}_\theta (x)= p(y=i|x;\theta) (i=1,2,3...k)$，在预测时，将自变量x带入每一个预测模型中，选择P最大的模型，找出相应的类别