[luogu p5658] 括号树

传送门

括号树

题目背景

本题中合法括号串的定义如下：

() 是合法括号串。
如果 A 是合法括号串，则 (A) 是合法括号串。
如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 \(l\) 与终止位置 \(r\) 来表示，记为 \(S (l, r)\)（\(1 \leq l \leq r \leq |S |\)，\(|S |\) 表示 S 的长度）。
S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 \(l\) 不同或 \(r\) 不同。

题目描述

一个大小为 \(n\) 的树包含 \(n\) 个结点和 \(n − 1\) 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 \(n\) 的树，树上结点从 \(1\) ∼ \(n\) 编号，\(1\) 号结点为树的根。除 \(1\) 号结点外，每个结点有一个父亲结点，\(u\)（\(2 \leq u \leq n\)）号结点的父亲为 \(f_u\)（\(1 ≤ f_u < u\)）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 \(s_i\) 为：将根结点到 \(i\) 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 \(s_i\) 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 \(i\)（\(1\leq i\leq n\)）求出，\(s_i\) 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 \(s_i\) 共有 \(k_i\) 个不同子串是合法括号串，你只需要告诉小 Q 所有 \(i \times k_i\) 的异或和，即：

\[(1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n) \]

其中 \(xor\) 是位异或运算。

输入输出格式

输入格式

第一行一个整数 \(n\)，表示树的大小。

第二行一个长为 \(n\) 的由( 与) 组成的括号串，第 \(i\) 个括号表示 \(i\) 号结点上的括号。

第三行包含 \(n − 1\) 个整数，第 \(i\)（\(1 \leq i \lt n\)）个整数表示 \(i + 1\) 号结点的父亲编号 \(f_{i+1}\)。

输出格式

仅一行一个整数表示答案。

输入输出样例

输入样例 #1

5
(()()
1 1 2 2

输出样例 #1

说明

【样例解释1】

树的形态如下图：

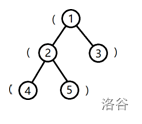
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 \(0\)。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 \(0\)。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 \(1\)。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 \(0\)。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 \(1\)。

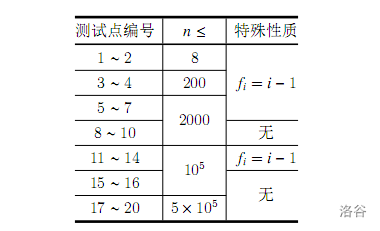
【数据范围】

CSP 2019 D1T2

分析

刷基础数学题单刷累了，来水水去年提高D1T2。

去年我还是一个菜鸡，连暴力都不会，但现在的我，哼哼，~~啊啊啊啊啊啊啊啊啊~~早已不是当年那个菜鸡了，~~是比当年还菜的菜鸡~~，再看到这道题我就有思路了。

做这种题，如果不是一眼正解的，一定要从部分分出发，慢慢向满分进军。

纯链暴力

观察到数据范围中有一个 \(f_i = i - 1\)。这是什么意思呢？也就是说这棵树是一条链。

问题就可以转化为，给你一个括号串 \(S\)，对于每一个 \(S(1, i)\)，求该子串的合法括号子串数量，并进行一些奇怪的运算（就是那个什么xor的）。

奇怪的运算不是重点，重点是我们怎么求重点加粗的内容。

显然我们可以暴力：枚举 \(i\) 从 \(1 \rightarrow n\)，用来锁定 \(S(1, i)\)，然后再在该子串中枚举左边界和右边界 \(l\) 和 \(r\)，锁定 \(S(l, r)\) 这个子串，接着再判断这个字符串是否是合法括号串。核心就是以上，至于计算什么的就略了。

\(i, l, r\) 三重循环，里面再套一个判断合法括号串，时间复杂度为 \(\operatorname{O}(n ^ 4)\)。来看看这个时间复杂度能过多少数据：

\(n \le 8\) 的肯定有戏。能通过1，2数据。

\(n \le 200\) 的话……如果是严格 \(n ^ 4\) 应该会T的，但是实际上算法跑不满 \(n ^ 4\)，所以有望能通过，但不知可否。

\(n \le 2000\) 及更高的就洗洗睡吧。这个 \(n ^2\) 都悬。

在CSP考场上，你就可以这样估分了。该算法最低10pts，最高20pts。当然前提是不写挂。

但是既然我们不在CSP考场，那咱们不妨试一试能得多少分：

（dbxxx花了5分钟打暴力，20分钟调bug后）

R39230100

真不戳，得到了20pts，是我们的期望最高值。

但是咱们肯定不能满足在20pts停滞不前呀！继续！

纯链算法优化

如果你是一个细心的孩子，你会发现纯链的数据点有 \(11\) 个，而我们通过了其中的 \(4\) 个，如果我们能再拿下剩下那 \(7\) 个，能得到 \(55 pts\)。这是非常友好的一个分了。

怎么优化呢？

观察数据范围是 \(5 \times 10 ^ 5\)，要不然 \(n \log n\)，要不然 \(n\)。

发现每次暴力算 \(k_i\) 时间复杂度无法承受，思考用递推求 \(k_i\)。

来举几个例子：

例子1

()()()

定义 \(con_i\) 为 \(i\) 对 \(k_i\) 的贡献值。

显然，当 \(i \le j\) 时，\(k_i \le k_j\)，说明我们应该从前往后推。

当 \(i = 1\) 时，只有一个左括号，没有办法形成合法括号序列。因此 \(con_1 = 0\)。
当 \(i = 2\) 时，发现了一个新合法括号序列 \(S(1, 2)\)，\(con_2 = 1\)。
当 \(i = 3\) 时，没有发现新的合法括号序列。\(con_3 = 0\)。
当 \(i = 4\) 时，发现了两个新合法括号序列 \(S(1, 4)\) 和 \(S(3, 4)\)。因此 \(con_4 = 2\)。
当 \(i = 5\) 时，没有发现新的合法括号序列。\(con_5 = 0\)。
当 \(i = 6\) 时，发现了三个新合法括号序列 \(S(1, 6)\)、\(S(3, 6)\) 和 \(S(5, 6)\)。因此 \(con_6 = 3\)。

\(con\) 数组的值为：
\(0, 1, 0, 2, 0, 3\)。

根据 \(k_i = \sum _{i = 1} ^ kcon_i\)，可得 \(k\) 数组的值为：\(0, 1, 1, 3, 3, 6\)。

另外我们还发现，\(S_i =\)（的时候，\(con_i = 0\)。原因很简单，在后面插一个左括号，不可能让合法括号序列的数量增加。

因此此后的举例中，将略过这些左括号的 \(con\) 值计算。

例子2

这次我们来在中间插个障碍吧：

())()

当 \(i = 2\) 时，发现了一个新合法括号序列 \(S(1, 2)\)，\(con_2 = 1\)。
当 \(i = 3\) 时，没有发现新的合法括号序列。\(con_3 = 0\)。
当 \(i = 5\) 时，发现了一个新合法括号序列 \(S(4, 5)\)，\(con_5 = 1\)。

你会发现，因为中间那个突兀的右括号存在，\(S(1, 5)\) 不再是一个合法括号序列了。

记住这个例子哦。

\(con\) 数组的值为：\(0, 1, 0, 0, 1\)；

\(k\) 数组的值为：\(0, 1, 1, 1, 2\)。

例子3

这次我们在中间插个反的：

()(()

当 \(i = 2\) 时，发现了一个新合法括号序列 \(S(1, 2)\)，\(con_2 = 1\)。
当 \(i = 5\) 时，发现了一个新合法括号序列 \(S(4, 5)\)，\(con_5 = 1\)。

\(con\) 数组的值为：\(0, 1, 0, 0, 1\)；

\(k\) 数组的值为：\(0, 1, 1, 1, 2\)。

和上面那个差不多，只是中间那个括号反了而已，省了一个计算 \(con\)。

例子4

合法括号串还可以嵌套，我们来看看嵌套的情况如何。

()(())

当 \(i = 2\) 时，发现了一个新合法括号序列 \(S(1, 2)\)，\(con_2 = 1\)。
当 \(i = 5\) 时，发现了一个新合法括号序列 \(S(4, 5)\)，\(con_5 = 1\)。

在 \(i = 5\) 前，你会发现这就是例子3。但是到 \(i = 6\) 呢？

当 \(i = 6\) 时，发现了两个新合法括号序列 \(S(1, 6)\) 和 \(S(3, 6)\)，\(con_6 = 2\)。

\(con\) 数组的值为：\(0, 1, 0, 0, 1, 2\)；

\(k\) 数组的值为：\(0, 1, 1, 1, 2, 4\)。

好了，例子都举完了，你发现什么规律了吗？

对于一个匹配了的右括号 \(R_1\)，如果这个匹配的括号的左括号 \(L_1\) 的左边，还有一个匹配了的右括号 \(R_2\)（这句话有点绕，稍微理解下），那么 \(R_1\) 的 \(con\) 值，等于 \(R_2\) 的 \(con\) 值 \(+1\)（即 \(con_{R_1} = con_{R_2} + 1\)）。

如何理解这个规律呢？

来看看合法括号串的第三条性质（就在题面的最上面）：

如果 A，B 是合法括号串，则 AB 是合法括号串。

\(L_1 \sim R_1\) 代表的这个括号串就相当于性质中的 \(B\) 串；\(L_2 \sim R_2\) 代表的括号串就相当于性质中的 \(A\) 串。如果 \(R_2\) 在 \(L_1\) 的左边且位置是挨着的，那么 \(AB\) 是合法括号串，因此 \(R_1\) 的贡献值还得多加一个 \(AB\) 这个串。

此处请一定要理解透彻，再慢理解也一定要理解透彻，因为这个规律对递推出结果非常重要，可以说是该算法的心脏。

好了，现在所有的问题都被解决了。就差一个问题：

我找到 \(R_1\) 了，我怎么找 \(L_1\)？压入栈的是括号，也没法找位置啊？

少年，思想别那么固执。既然要找位置，那么就把压括号改成压位置不就完了吗？

核心代码如下：

for (int i = 1; i <= n; ++i) {
    if (str[i] == '(')
        bra.push(i);
    else if (!bra.empty()){
        num = bra.top();
        bra.pop();
        con[i] = con[num - 1] + 1;
    }

    k[i] = k[i - 1] + con[i];
}

时间复杂度 \(\operatorname{O}(n)\)。

和预期一样，能获得 \(55pts\) 的友好分。评测记录

正解

接下来我们就来进军正解吧。

从链变到树，con[i] = con[num - 1] + 1; 这个递推式就有问题了。因为在链中，编号是连续的，因此我们可以直接num - 1。但是树的编号可就不连续了。

那么怎么改递推式呢？其实非常简单，把num - 1改成fa[num]就可以了。

很好理解，因为括号树是从根不断往下的，因此如果想找一个节点的上一个，显然就是其父亲节点。链中的num - 1其实就相当于fa[num]嘛！

当然了，\(k_i\) 的递推式也得改了，k[i] = k[i - 1] + con[i] 应该变为 k[i] = k[fa[i]] + con[i]。

但是这样就结束了吗？

链的遍历直接从 \(1 \rightarrow n\) 就可以了，但是树的遍历有回溯。那么在进行dfs的过程中，栈也得复原。

这样，我们就能拿到 \(100pts\) 的满分了！

核心代码如下：

void dfs(int u) {
    int num = 0;
    if (str[u] == '(')
        bra.push(u);
    else if (!bra.empty()){
        num = bra.top();
        bra.pop();
        con[u] = con[fa[num]] + 1;
    }

    k[u] = k[fa[u]] + con[u];
    for (int i = 0; i < G[u].size(); ++i)
        dfs(G[u][i]);
    
    if (num != 0)
        bra.push(num);
    else if (!bra.empty())
        bra.pop();
    //复原
    //就是上边栈的操作反过来就可以了
    return ;
}

最后的最后，别忘了，不开longlong见祖宗！！！！！！！

好了，接下来我们来上一下三种方法的整体代码，供大家参考。

代码

\(\operatorname{O}(n ^ 4)\)，仅支持链算法代码

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2020-10-04 12:10:42 
 * @Last Modified by: crab-in-the-northeast
 * @Last Modified time: 2020-10-04 13:35:50
 */
#include <iostream>
#include <cstdio>
#include <string>

typedef long long ll;

const int maxn = 500005;//尽管我们知道该算法通过不了500005数量级的，但maxn建议还是开到最大值。万一能通过比200大的数据，但是因为开的不够大挂了，那就很可惜了。
int fa[maxn];
ll k[maxn];

bool check(std :: string str) {
    //std :: cout << str << std :: endl;
    int status = 0;
    for (int i = 0; i < str.length(); ++i) {
        if (str[i] == '(') ++status;
        else --status;
        if (status < 0) return false;
    }
    if (status == 0) return true;
    return false;
}//判断合法括号串可以看P1739。

int main() {
    int n;
    std :: string str;
    std :: scanf("%d", &n);
    std :: cin >> str;
    str = ' ' + str;
    for (int i = 2; i <= n; ++i)
        std :: scanf("%d", &fa[i]);
    
    for (int i = 1; i <= n; ++i)
        for (int l = 1; l <= i; ++l)
            for (int r = l; r <= i; ++r)
                if (check(str.substr(l, r - l + 1)))
                    ++k[i];
    
    //for (int i = 1; i <= n; ++i)
        //std :: printf("%lld ", k[i]);
    
    ll ans = 0;
    for (int i = 1; i <= n; ++i)
        ans ^= k[i] * ll(i);
    
    std :: printf("%lld\n", ans);
    return 0;
}

\(\operatorname{O}(n)\)，仅支持链算法代码

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2020-10-04 12:10:42 
 * @Last Modified by: crab-in-the-northeast
 * @Last Modified time: 2020-10-04 12:32:26
 */
#include <iostream>
#include <cstdio>
#include <string>
#include <stack>

typedef long long ll;

const int maxn = 500005;
int fa[maxn];
ll k[maxn], con[maxn];

std :: stack <int> bra;

int main() {
    int n;
    std :: string str;
    std :: scanf("%d", &n);
    std :: cin >> str;
    str = ' ' + str;
    for (int i = 2; i <= n; ++i)
        std :: scanf("%d", &fa[i]);
    
    for (int i = 1; i <= n; ++i) {
        if (str[i] == '(')
            bra.push(i);
        else if (!bra.empty()){
            int num = bra.top();
            bra.pop();
            con[i] = con[num - 1] + 1;
        }

        k[i] = k[i - 1] + con[i];
    }
    
    //for (int i = 1; i <= n; ++i)
        //std :: printf("%lld ", k[i]);
    
    ll ans = 0;
    for (int i = 1; i <= n; ++i)
        ans ^= k[i] * ll(i);
    
    std :: printf("%lld\n", ans);
    return 0;
}

\(\operatorname{O}(n)\)，满分算法

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2020-10-04 10:27:40 
 * @Last Modified by: crab-in-the-northeast
 * @Last Modified time: 2020-10-04 11:53:50
 */
#include <iostream>
#include <cstdio>
#include <vector>
#include <stack>

typedef long long ll;
const int maxn = 500005;

std :: vector <int> G[maxn];
std :: stack <int> bra;

char str[maxn];
int fa[maxn];
ll con[maxn], k[maxn];

void dfs(int u) {
    int num = 0;
    if (str[u] == '(')
        bra.push(u);
    else if (!bra.empty()){
        num = bra.top();
        bra.pop();
        con[u] = con[fa[num]] + 1;
    }

    k[u] = k[fa[u]] + con[u];
    for (int i = 0; i < G[u].size(); ++i)
        dfs(G[u][i]);
    
    if (num != 0)
        bra.push(num);
    else if (!bra.empty())
        bra.pop();
    return ;
}

int main() {
    int n;
    std :: scanf("%d", &n);
    std :: scanf("%s", str + 1);
    for (int i = 2; i <= n; ++i) {
        std :: scanf("%d", &fa[i]);
        G[fa[i]].push_back(i);
    }
    ll ans = 0;
    dfs(1);
    for (int i = 1; i <= n; ++i)
        ans ^= k[i] * (ll)i;
    std :: printf("%lld\n", ans);
    return 0;
}

评测记录

后记 & 有感

遇到这种一眼没正解的题目，不要慌，

一定要从部分分入手，逐渐进军，

比如本题就是从链暴力->链优化->正解逐一击破的

最后，在CSP的考场上，一定别轻言放弃

CSP给的时间是足够的，

所以一开始直接想满分的，是非常愚蠢的做法，除非一眼正解。

另外，注意数据范围是不是要开longlong，

最后CSP临近，东北小蟹蟹祝大家\(CSP_{2020}++\)！

本篇题解花了我两个小时的时间，是我写过的最详细的一篇题解了吧。233

posted @ 2020-10-04 14:08 dbxxx 阅读(179) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

dbxxx

你好！欢迎来访我的博客。