计算机组成原理 I 学习笔记（大一第二学期）

学习资料：Noam Nisan vs Shimon Schocken, The Elements of Computing Systems Building a Modern Computer from First Principles / nand2tetris

完成进度：10%

本文为第一部分，对应 nand2tetris 课程设置的硬件部分．

导引

用高级语言写成的再简单的代码，如 Hello World, 在机器的眼中也只是一串陌生而不可读的文本．执行该程序前，必须先解析这些高级的字符串，揭示其语义（semantics），即理解程序期望实现的功能，然后根据目标计算机的机器语言，生成能重新表达该语义的低级代码．这个复杂的翻译过程称作编译，其产物将是一串可执行的机器语言指令序列．

机器语言一般是一组计算机能理解的二进制代码，但其本身也是一种抽象．如果再向具体的方向走就来到了硬件．计算机通过硬件体系理解二进制代码．硬件体系由芯片组构成，包含寄存器（register）、内存单元、算术逻辑单元（Arithmetic Logic Unit, ALU）等．其中的每个芯片由基本逻辑门构成．基本逻辑门又由 nand 这样的原始门构成．原始门由若干个转换设备构成，通常是用晶体管实现的．到这里就是计算机组成原理下沉研究的尽头了，因为晶体管具体的构成已经属于物理方向了．

• 所有的逻辑门都可以只用 nand 门来构建．
• 在软件层次，所有高级语言都依赖一套翻译工具（编译器/解释器 complier / interpreter、虚拟机、汇编器 assembler），将高级代码逐步降级为机器级指令．有些高级语言采用解释执行而非编译（如 Python），有些则无需虚拟机，但整体架构的本质是相同的．
• 计算机科学的一个基本原理是 Church-Turing 猜想：从根本上说，所有计算机在本质上是等价的．

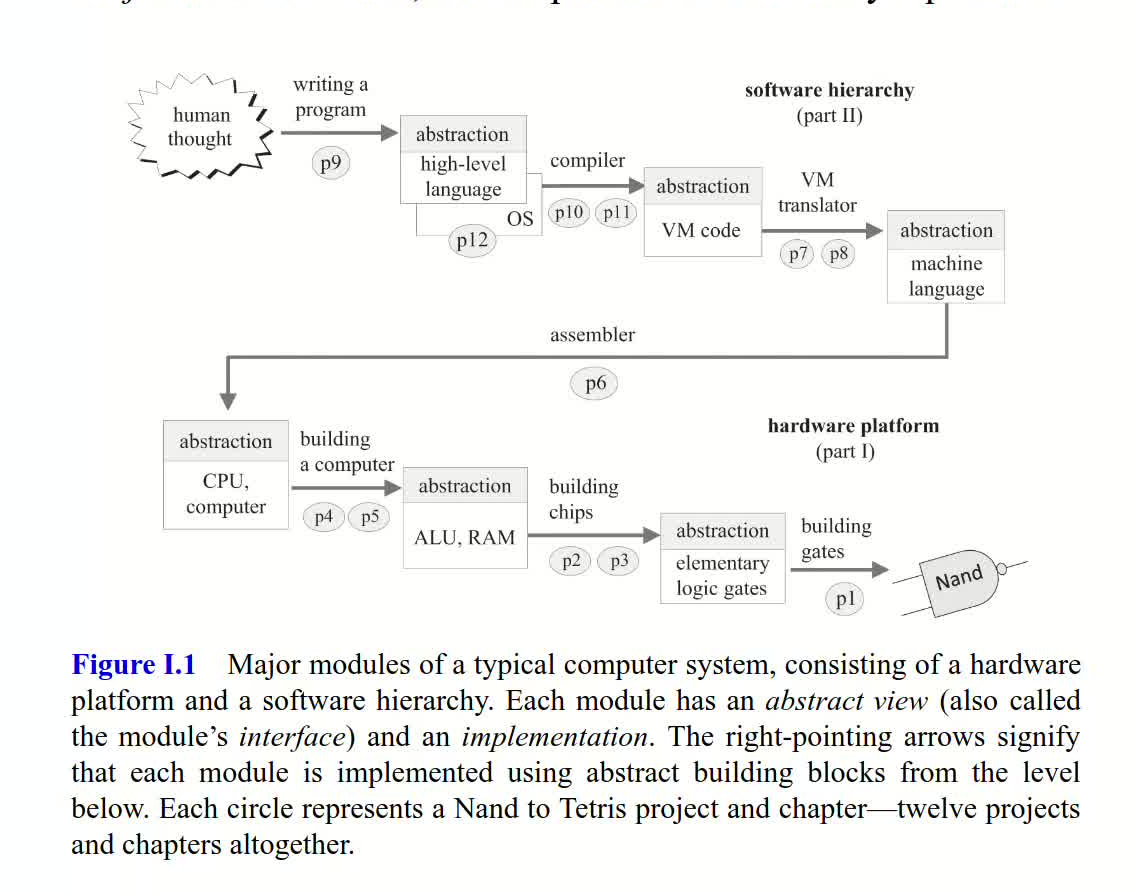
nand2tetris 这门课程的硬件部分的目标是构造一个名为Hack的简易计算机，软件部分的目标是实现一个名为Jack的语言．简易性可以为教学提供极大的方便．

自上而下和自下而上是会经常遇到的两种描述方式．自上而下通常展示高级抽象如何被简化为或由更简单的抽象实现．例如，可以描述二进制机器指令是如何分解为微代码的，这些微代码又是怎样流经体系结构的线路，最终操控底层的 ALU 和 RAM 芯片的．或者，我们也可以自下而上地描述，如何通过巧妙设计 ALU 和 RAM 芯片来执行微代码，而这些微代码又如何共同构成了二进制机器指令．自上而下与自下而上两种视角都极具启发性，在不同的视角切换有助于学习计算机组成原理．

学习计算机组成原理的关键是处理好直接面向一个精细，复杂的结构进行学习的困难．应对这种复杂性，我们的处理是模块化．每个模块会在独立的章节分别描述，并在独立的章节分别完成实现．很明显，模块之间并不是完全独立的，故良好的模块化设计，应当能做到独立处理单个模块的时候，可以暂时忽略其他部分．这样一来，只要系统的模块化设计得当，我们可以以任意的顺序构建模块，这也为团队合作提供极大的便利．现代计算机很成功的做到了这一点，nand2tetris 课程也做到了这一点．

模块化的关键是明确并区分抽象层（abstraction）和实现层（implementation）．

• 抽象描述模块做什么．
• 实现描述模块怎么做的．

然后就是系统工程中最重要的准则：将任何模块作为构建单元使用时，必须专注其抽象层描述，而完全忽略其实现细节．用更通俗的话，用 \(A\) 实现 \(B\) 时，只需知道 \(A\) 的作用（抽象层），而不需，也为了人脑健康着想，不要在意 \(A\) 是怎么实现的（实现层）．因此这种准则有时候也称作黑盒准则（相信 \(A\) 是一个能完成目的的黑盒）．类似写递归的时候，必须明确相信这个函数能做到什么功能（抽象层），而不是再次没完没了地深入细节．虽然系统工程不是递归而是有限层级的，但是人脑能压几层栈？

进行合理的模块化设计（具体设计哪些模块）需要多见多练．好的大项目一定有非常合理的模块化设计，这样才可易于维护．

本文是 nand2tetris 的第一部分：设计硬件平台．第二部分是设计软件架构，会另开一篇文章．

硬件平台基于大约 30 种逻辑门和芯片构建．这些门电路与芯片——包括最顶层的计算机体系结构——都将使用硬件描述语言（Hardware Description Language, HDL）实现，我们将通过运行在 PC 上的硬件模拟器来测试 HDL 程序的正确性．这正是硬件工程师实际工作的方法：借助软件模拟器构建并测试芯片设计，当芯片在模拟中的表现达到预期后，便将设计规范（HDL 程序）交付给芯片制造公司。经过优化，这些 HDL 程序将成为控制机械臂的输入指令，最终在硅基材料上制造出实体硬件．

在第二部分，我们将构建包括汇编器、虚拟机、编译器在内的软件栈．这些程序可用任何高级编程语言实现．此外，我们还将开发一个用 Jack 语言编写的基础操作系统．

nand2tetris 的章节顺序是从下而上的．我们从基础逻辑门开始，逐步向上构建，最终导向一种高级的、基于对象的编程语言．与此同时，每个模块的开发是从上而下的——我们使用下一层的模块（只考虑其抽象层）进行当前的模块的实现，从而完成当前模块的抽象．下面是第一部分的蓝图．

• 第一章，我们从单个逻辑门，nand 门出发，用它构建出一系列基础常用的逻辑门，例如 and 门、or 门、xor 门等．
• 在第二、三章中，我们将用这些基础模块分别构建一个算术逻辑单元（ALU）和一系列存储设备．
• 第四章我们将暂时停下硬件构建的脚步，介绍一种包含符号形式和二进制形式的低级机器语言．
• 第五章则利用之前构建的 ALU 和存储单元，搭建一个中央处理器（CPU）和随机存取存储器（RAM）．这些设备随后将被集成为一个能够运行第四章所介绍的机器语言程序的硬件平台．
• 第六章我们将描述并构建一个汇编器（assembler），这是一个能将用符号机器语言编写的低级程序翻译成可执行二进制代码的程序．

至此，硬件平台的构建将宣告完成．这个平台将成为第二部分的起点，在那里我们将用一个由虚拟机、编译器和操作系统构成的现代软件体系来扩展这个核心硬件．

布尔逻辑

涉及到的层级：芯片由基本逻辑门构成，基本逻辑门由nand 门构成，这章探讨nand 门构造基本逻辑门．

布尔代数

一个二元逻辑运算符总共有多少种？答案是 \(16\) 种．

我们知道三种最基本的运算符是与，或和非．前两者是二元逻辑运算符（因此是上面的 \(16\) 种之一），非则是一元的．这三种运算符之所以基本，是因为从这三种逻辑运算符出发，可以构造任何一个布尔函数．换言之，这三种运算符足以张成任何需要的逻辑运算．

事实上，三种不是最少的需求，一种就够了．我们只需要一个nand 运算符，即可构造任何一个布尔函数．

这里，布尔函数是将 \(n\) 个布尔值映射到 \(1\) 个布尔值的函数，即 \(\{0, 1\}^n \mapsto \{0, 1\}\)．二元逻辑运算符 是 \(n = 2\) 的情形．\(n\) 元布尔函数总共有 \(2^{2^n}\) 种．

布尔函数有两种表达方式．一种是真值表（truth table），枚举 \(n\) 个变元取遍 \(2^n\) 种布尔值的情形，再在每种情形最后标记布尔函数的结果．一种是逻辑表达式．\(n\) 元布尔函数都可以表示成用二元逻辑运算符串联起来的表达式，正确性在笔者的直觉里是明显的，但证明应该要花一些时间，后面感兴趣的话补一下．

在构建计算机时，真值表、逻辑表达式以及两者相互转换的能力都至关重要．通常我们的目标是在硬件层面设计一个满足某个真值表的布尔函数，从给定的真值表数据为起点，我们可以综合出一个表征底层函数的逻辑表达式．通过布尔代数简化该表达式后，我们就能如本章后续所示，用逻辑门来实现它．总而言之，真值表通常是描述某些自然状态的便捷工具，而布尔表达式则是在硅基硬件中实现该描述的便利形式．在两种表示法之间灵活转换的能力，是硬件设计最重要的实践之一．

另外，同一布尔函数的真值表是唯一的，但逻辑表达式不唯一．这些逻辑表达式相互不同却等价，可能会有不同的复杂度．我们倾向于更简洁，更易于处理的表达式．简化逻辑表达式的能力是实现硬件优化的第一步，需要运用布尔代数和逻辑直觉来完成．

逻辑门

门（gate）是支持简单布尔函数的物理设备，通常通过晶体管包装成芯片（chip）的形式实现．nand2tetris 这门课不区分门和芯片两个术语．唯一的区分是，芯片通常指的是更复杂的门．

与，或，非三种初始门（primitive gate）的实现是我们不必关心的，交给电子工程师即可．用初始门构造出复合门（composite gate），进一步制造出更复杂的芯片是计算机组成原理的课题．

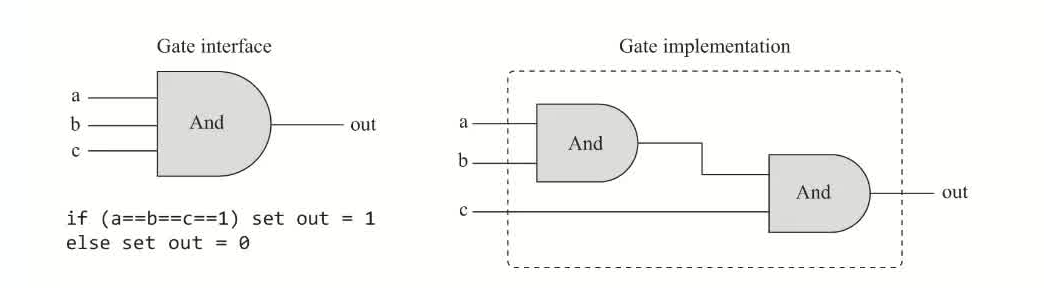
左侧是抽象层（abstraction），有时候也被称作接口层（interface），右侧是实现层（implementation）．同一种逻辑门的抽象层唯一，但实现层可以有多种．用到的初始门越少，实现越优秀，通常意味着更低的成本，更少的能量和更快的计算速度．

换言之，逻辑门设计的艺术是：给定目标门的抽象层，找到一种尽量高效的实现方式，而材料正是已经实现好的门．

硬件制造方式

很明显，如今的硬件不可能通过纯手工制造的方式进行．极不易查错也不好调试．硬件工程师如今设计芯片结构的方式如下：

• 使用HDL编程，实现芯片逻辑（即芯片具体是怎么用逻辑门组合完成任务的）．
• 采用硬件模拟器（hardware simulator），通过大量的输入测试，检查输出是否满足预期效果．即，通过大量测试检验芯片正确性．
• 硬件模拟器在验证正确性的同时，还可帮助模拟和量化一些参数，比如计算效率，能量损耗以及成本等，帮助硬件设计师保证正确性的同时，对芯片进行进一步的优化．
• 然后把这份HDL程序外包给芯片制造公司让他们量产，这就不是我们的任务了．

逻辑门说明

nand, and, or, xor, not．意义显然．

复用器（multiplexer）．

name: Mux
input: a, b, sel
output: out
function: if sel == 0 then out = a, else out = b

分配器（demultiplexer）．

name: DMux
input: in, sel
output: a, b
function: if sel == 0 then {a, b} = {in, 0} else {a, b} = {0, in}

多位 or， 多位 and, 多位 xor 以多位 or举例．

name: Or16
intput: a[16], b[16]
output: out[16]
function: for i = 0..15 out[i] = Or(a[i], b[i])

多位复用器（multi-bit multiplexer）：

name: Mux16
input: a[16], b[16], sel
output: out
function: if sel == 0 then for i = 0..15 out[i] = a[i], 
	else for i = 0..15 out[i] = b[i]

多路 or（multi-way or）：

name: Or8Way
intput: in[8]
output: out
function: out[i] = Or(in[0], in[1], ..., in[7])

多路多位复用器（multi-way multi-bit multiplexer）：

多路指的是选择的变量数，多位指的是每个待选变量的位数．

我们的计算机会用到 4-way 16-bit 和 8-way 16-bit，以前者举例．

name: Mux4Way16
input: a[16], b[16], c[16], d[16], sel[2]
output: out[16]
function: if (sel == 00, 01, 10, or 11) then out = a, b, c, or d
comment: = is a 16-bit assignment operation

多路多位分配器（multi-way multi-bit demultiplexer）：

我们的计算机会用到 4-way 1-bit 和 8-way 1-bit，以前者举例．

name: DMux4Way
input: in, sel[2]
output: a, b, c, d
function:
if (sel == 00) then {a, b, c, d} = {1, 0, 0, 0},
elif (sel == 01) then {a, b, c, d} = {0, 1, 0, 0},
elif (sel == 10) then {a, b, c, d} = {0, 0, 1, 0},
else then {a, b, c, d} = {0, 0, 0, 1}