线性代数学习笔记（大一第一学期）

课程资料：Gilbert Strang, Introduction to Linear Algebra.

完成进度：85%

导引

向量无特殊说明，均指列向量．

线性组合．\(n\) 个 \(m\) 维向量的线性组合，是 \(\R ^m\) 的一个子空间．这个子空间的维数 \(r \le \min(n, m)\)．三维子空间可以抽象为空间，二维是平面，一维是直线，零维是点．注意：线性空间必须包含零元，即上面抽象出来的几何结构都必须经过原点．

\(r \le \min(n, m)\) 的一些例子：

• \(2\) 个一维向量最多张成一条直线．
• \(1\) 个二维向量最多张成平面内的一条直线．
• \(2\) 个二维向量最多张成整个平面，但也有可能只能张成一条线（共线时）．

方程．线性代数面向一次方程．所有的一次方程都可以化为线性表达式 = 右值的形式，多个方程的右值构成右值组（为了方便叙述自定义的概念）．比如

\[\begin{cases} 2x_1 + 3x_2 = -1 \\ 2x_1 - 3x_2 = 5 \end{cases} \]

包含两个式子和两个右值，\(2x_1 + 3x_2\) 是其中一个式子，\(5\) 是另一式子的右值．

右值组一般对应列向量．如这里右值组适合被理解为 \(\bm b = (-1, 5)\)．本文约定 \((a, b, c, \ldots)\) 表示列向量．

线性表达式是 \(n\) 元一次，不含常数的多项式．其系数可以被刻画为行向量．如第一个方程对应的行向量为 \(\bm r = \begin{bmatrix}2 & 3\end{bmatrix}\)．

一组解一般对应列向量．如上述方程的解可表示为 \(\bm x = (1, -1)\)．

解向量维数等于线性表达式向量维数．因为它们都是变元的数量．

右值组维数等于线性表达式向量的数量．因为它们都是方程的数量．

将一个解 \(\bm x\) 代入单个线性表达式，得到一个右值的过程，事实上是求解 \(\bm r \cdot \bm x\) 的过程．一组解代入单个线性表达式得到右值，本质是在求点积．

矩阵．将 \(n\) 个 \(m\) 维向量放在一起，就变成了一个 \(m \times n\) 的矩阵（\(n\) 和 \(m\) 的命名习惯与 OI 恰好是相反的）．矩阵 \(A\) 的每个行向量理解为线性表达式向量，同时，\(A\) 的列向量也有美丽的意义，马上揭晓．

将一组解代入一个方程组的过程，形如

\[A \bm x = \bm b \]

这个式子有非常多的视角，具体而言：

• 从 \(\bm x\) 对 \(A\) 作用的视角一：\(A\) 包含 \(m\) 个线性表达式系数行向量，\(n\) 个分量分别对应该表达式 \(n\) 个变元的系数．每一行与 \(\bm x\) 点积，得到这个式子在解 \(\bm x\) 下的右值，并构成一个完整的方程．\(\bm x\) 的共 \(n\) 个分量是 \(n\) 个变元的值，\(\bm b\) 的共 \(m\) 个分量是每一个右值．称作行视角．在这个视角下，我们按行理解 \(A\)——每个行向量对应一个线性表达式．
• 小注：方程也可以视作一个几何结构．如二元方程是一条线，三元方程是一个平面．
• 从 \(\bm x\) 对 \(A\) 作用的视角二：\(A\) 的 \(n\) 列分别指 \(n\) 个列向量，则每一列的 \(m\) 个元素是自然指该向量的 \(m\) 个分量．此时，\(A \bm x = \bm b\) 可以视作将 \(A\) 的 \(n\) 个列向量线性组合成 \(\bm b\)．\(\bm x\) 中的 \(n\) 个分量是每个向量在这个线性组合中的系数，故这里 \(\bm x\) 的含义是线性组合方式．称作列视角．
• 从 \(A\) 对 \(\bm x\) 作用的视角：\(A\) 刻画了一种变换规则！它可以将一个 \(n\) 维向量转化为 \(m\) 维向量．如果这个变换是可逆的，则 \(A^{-1}\) 对应的就是逆变换规则．如 \(n = m\) 时的前缀和和差分操作，就可以用矩阵刻画，并且刻画出来的矩阵是互逆的．

一个式子有三个视角，体现了线性代数之美：

• 行视角思考的是 \(A\) 中每个行向量，是线性表达式系数行向量，则 \(\bm x\) 是一组解向量，\(\bm b\) 是一组右值向量，操作是多次点积得到多个右值构成右值组．
• 列视角思考的是 \(A\) 中的每个列向量，则 \(\bm x\) 是一个线性组合方式（具体表现就是线性组合中的系数），\(\bm b\) 则是一个线性组合结果，操作是对 \(A\) 的列向量线性组合得到 \(\bm b\)．

下面是一个对变换视角的思考．

矩阵可逆的意思，就是矩阵对应的变换是可逆的．换言之，对于任意一个 \(\bm b\)，只能存在一个 \(\bm x\) 使得 \(A \bm x = \bm b\)．否则，无法从 \(\bm b\) 的信息还原为 \(\bm x\)．

我们知道 \(A \bm 0 = \bm 0\)．因此，对于可逆矩阵 \(A\) 和零向量 \(\bm b\)，满足 \(A \bm x = \bm b\) 的 \(\bm x\) 只能是零向量．从列视角看，这意味着只有全零线性组合可以将 \(A\) 的列向量组合成零向量，证明了 \(A\) 的列向量线性无关，即没有列向量可以表为其它列向量的线性组合．故 \(A\) 列满秩．

其实 \(A\) 可逆还要求 \(A\) 行满秩．这是因为我们不仅要求可逆的唯一性，还要求可逆的存在性，上面只利用了可逆性质的一半，故只推出满秩性质的一半，理故宜然．剩下一半性质的讨论将在后面深入研究．

解线性方程组

本章默认 \(n = m\)．因为我们重点关注怎么解，所以重点研究的都是解大概率唯一的方程组，这要求变元数量 \(n\) 等于方程数量 \(m\)．当然，这样的方程组一定有解，但不一定有唯一解．有唯一解与矩阵可逆对应，无唯一解与矩阵不可逆对应（这是刚刚讨论过的内容）．

Gauss-Jordan 消元

下面研究如何解 \(A \bm x = \bm b\)．有 \(\bm x = A^{-1}\bm b\)，但 \(A^{-1}\) 的求解复杂度与解方程相同．答案都是 Gauss-Jordan 消元．

Gauss 负责 \(A \to U\)，Jordan 负责 \(U \to R\)．特别地，若矩阵可逆，则这里的 \(R\)（ref,行阶梯形矩阵）即 \(D\)（对角阵）．

Gauss 的流程是：进行可能的 \(\Theta(n)\) 次置换操作，和 \(\Theta(n^2)\) 次倍加操作．

Gauss:
for i: 1 to n
	if a[i][i] = 0, then swap a[j] and a[i] s.t. a[j][i] != 0
	use a[i] eliminate all a[j][i] s.t. j > i

Jordan:
for i: 1 to n
	use a[i] eliminate all a[j][i] s.t. j < i

so Gauss-Jordan:
for i: 1 to n
	if a[i][i] = 0, then swap a[j] and a[i] s.t. a[j][i] != 0
	use a[i] eliminate all a[j][i] s.t. j != i

(In computation, for smaller error purpose, choose the a[j] with maximum a[j][i],
and swap it with a[i])

Gauss-Jordan 只会用到倍加和行置换两种操作．这两种操作都可以刻画为左乘矩阵，前者称作倍加矩阵，后者称作置换矩阵，我们另有数乘矩阵．这三种矩阵左乘对行操作，右乘对列操作，简称之，左行右列．

当我们对系数矩阵 \(A\) 进行操作时，也要对 \(b\) 进行同样的操作．所以我们又有增广矩阵的概念．只需将 \(\bm b\) 置于 \(A\) 的右侧，就可视作对矩阵 \([A \quad b]\) 操作．

矩阵乘法

上面用到了矩阵乘法的概念，事实上矩阵乘法也有很多种视角．朴素的定义是 \(C(i, j)\) 是 \(A\) 的第 \(i\) 行与 \(B\) 的第 \(j\) 列点乘的结果．但是，我们还可以将矩阵乘法视作多个矩阵与向量相乘，而这是导引讨论过的内容．

具体而言，\(A \times B = C\)，

• \(C\) 的第 \(i\) 行与 \(A\) 的第 \(i\) 行和整个 \(B\) 有关．它是 \(\bm{row(i)} \times B\)．
• \(C\) 的第 \(j\) 列与整个 \(A\) 和 \(B\) 的第 \(j\) 列有关．它是 \(A \times \bm{col(j)}\)．

我们知道 \(A \times \bm x\) 有三种视角，那么矩阵乘法总共会出现六种视角．先以比较熟悉的形式，\(A \times \bm{col(j)}\) 为例．这也就是说：

• 左行右列视角：对 \(A\) 的每一行视作线性表达式的系数行向量，\(\bm{col(j)}\) 视作一个解向量．多组解，可以得到多个右值组，组合为矩阵 \(C\)．
• 左列右列视角：对 \(A\) 的每一列视作列向量．则一个 \(\bm{col(j)}\) 对应一种线性组合方式．多个线性组合方式得到多个列向量，组合为矩阵 \(C\)．
• 左乘变换视角：\(A\) 是变换操作，它对 \(B\) 的每个列向量 \(\bm{col(j)}\) 打包变换，变换结果按原来的顺序组合成矩阵 \(C\)．

事实上，\(\bm{row(i)} \times B\) 的原理是完全相同的，只不过这次我们要把行和列的意义置换一下．我相信这个简单的小操作应该难不倒读者．

• 左列右行视角：对 \(B\) 的每一列视作线性表达式系数列向量，而一个 \(\bm{row(i)}\) 是一组解行向量．多组解，可以得到多个右值组行向量，组合成矩阵 \(C\)．
• 左行右行视角：对 \(B\) 的每一行视作一个行向量，而一个 \(\bm{row(i)}\) 对应一种线性组合方式．多个线性组合方式得到多个行向量，组合为矩阵 \(C\)．
• 右乘变换视角：\(B\) 也是一种变换操作．它对 \(A\) 中每个行向量 \(\bm{row(i)}\) 打包变换，变换结果按原来的顺序组合成矩阵 \(C\)．

不同的操作适合用不同的视角理解，如：

• 增广矩阵利用了左乘变换视角．我们注意到 \(A \times B\) 是对 \(B\) 的列向量打包变换，增广操作相当于对这个包再加入一个列向量，一起操作．
• 初等行变换利用了左行右行视角．我们将 \(B\) 视作多个行向量，通过设计 \(A\) 每一行的线性组合系数，构造出结果 \(C\) 的这一行行向量．

这里应该举例子，比如

\[P = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} \]

\(PB\) 可以将 \(B\) 的第二行与第三行置换．

\[E = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -3 & 0 & 1 \end{bmatrix} \]

\(EB\) 可以将 \(B\) 的第三行减去三倍的第一行．如果读者不能很快并精准地看出这一点，请重新复习上面那段话．

初等行变换是否能用左乘变换视角理解呢？答案是可以的，比如上面对 \(B\) 的第二行与第三行置换，其实就是把 \(B\) 的所有列向量第二分量和第三分量交换！这就是一种批量的变换．所以，这些视角不是分裂的，而是可以随意切换看待的．

初等列变换可以对应右乘变换视角（批量操作行向量的分量），也可以对应左列右列视角．

\(A \times B\) 还是 \(\bm{col_A(i)} \times \bm{row_B(i)}\) 的和．也就是 \(A\) 的每个列和 \(B\) 的每个行构成的 \(n\) 个张量积的和．称作张量积和视角．

分块矩阵

对矩阵任意画几条无限长横直线与无限长竖直线，可以将矩阵分块．如果：

• \(A\) 的宽度与 \(B\) 的高度相等．
• 对 \(A\) 画的竖线（将 \(A\) 的宽度切分），与对 \(B\) 画的横线（将 \(B\) 的高度切分），数量和切分结构完全相同．如对 \(A\) 画两条竖线，将宽为 \(4\) 的 \(A\) 划分成 \(1 + 2 + 1\)，则对 \(B\) 画的两条横线必须也将宽度切分为 \(1 + 2 + 1\)．
• 对 \(A\) 画的横线与对 \(B\) 画的竖线，数量相同即可．

根据这个原理，可以证明上面那个神奇的想法．我们只需要将 \(A\) 按每列分块，\(B\) 按每行分块，立即得到这个结论．

考虑用分块矩阵进行 Gauss 消元操作，我们可以得到一个叫舒尔补（Schur Complement）的东西．

\[\begin{bmatrix} I & 0 \\ -CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & B \\ C & D \end{bmatrix} = \begin{bmatrix} A & B \\ 0 & D - CA^{-1}B \end{bmatrix} \]

注意：对矩阵进行操作必须区分左右乘．行置换和倍加都是左乘．

逆矩阵

考虑同时对矩阵 \(A\) 与 \(I\) 进行 Gauss-Jordan 操作，将 \(A\) 对角化，即令 \(A \to D\)．这相当于我们对 \(A\) 左乘多次倍加矩阵 \(E\) 和置换矩阵 \(P\)，最后变为对角阵 \(D\)．

然后，我们对 \(D\) 进行一步归一化．左乘 \(D^{-1}\) 即可．设这些 \(E\)，\(P\)，以及最后 \(D^{-1}\) 矩阵的积（有顺序！矩阵乘法无交换律）为 \(M\)，则 \(MA = I\)．故 \(M\) 是 \(A\) 的逆．由于我们对 \(A\) 和 \(I\) 同步操作，则右侧的 \(I\) 将变为 \(MI = M\)，这就得到了 \(A\) 的逆矩阵 \(M\)．

上面操作可行的前提是 Gauss-Jordan 成功．若 Gauss-Jordan 失败，说明矩阵含有自由变元，证明矩阵是不可逆的．从行视角看，自由变元取不同的值，可以在相同的右值组下取到不同的解．换为列视角，则是不同的线性组合可以组合出相同的向量．这意味着向量一定线性有关．

矩阵在进行归一化前（即到达 \(D\) 时），\(D\) 对角线上的所有主元之积是 \(D\) 的行列式．\(P\)，\(E\) 等操作不改变行列式，因此 \(A\) 的行列式也是同一个值．矩阵可逆等价行列式不为 \(0\)．这是因为矩阵可逆等价于 Gauss-Jordan 的成功与否，其实就是最后归一化的成功与否．对角线上的主元都不为 \(0\) 则成功，有一个 \(0\) 则失败．

方阵 \(A\) 与 \(B\) 的逆均存在，等价于 \(AB\) 的逆存在．这里的等价性代表可以反推，即我们将一个可逆方阵分解为两个方阵之积，则这两个方阵也必可逆．

\[(AB)^{-1} = B^{-1}A^{-1} \]

这是因为撤销操作的时候应该是栈序的．

必须注意：这个式子有一个使用前提是 \(A\) 与 \(B\) 均是方阵．如果滥用这个规则，会导致非常致命的错误．

可以证明，方阵若有逆，则其两侧的逆一定相同．

\[BA = I, AC = I \implies B(AC) = (BA)C \implies BI = IC \implies B = C \]

非方阵矩阵似乎也可以套用这个证明？不可以！如果是非方阵矩阵，两个 \(I\) 不是同一大小的单位矩阵，这样做是完全错误的．必须注意2：逆必须满足 \(AA^{-1} = A^{-1}A = I\)．只有方阵才有逆．非方阵的矩阵 \(B\) 也可以有另一矩阵 \(C\) 满足 \(CB = I\)，这是单侧的逆，不能称作 \(B^{-1}\)．

上三角的逆是上三角，下三角的逆是下三角．考虑 Gauss-Jordan 求逆的过程：

上三角相当于没有 Gauss 操作，所以右侧的 \(I\) 变为上三角的逆的过程中，无 Gauss 操作，即下三角始终不会被影响，为初始的 \(0\)．故上三角的逆是上三角．下三角则是反过来，只有 Gauss 没有 Jordan.所以只会改变下三角元素．

有一种矩阵叫对角占优矩阵（diagonally dominant）．定义为满足下面性质的方阵．

\[\forall i, |a(i, i)| > \sum_{j = 1} ^ n |a(i, j)| \times [j \ne i] \]

这样的矩阵列向量一定线性无关，因此矩阵可逆．

LU 分解

提示两点：

• 讨论 LU 分解时，只讨论 \(A \to U\) 的过程，即 Gauss-Jordan 中的 Gauss，而通常不讨论 Jordan.
• 讨论 LU 分解时，默认 \(A\) 在进行 Gauss 操作时无需行置换．这等价于 \(A\) 的顺序主子式非零（如果不知道这是什么意思可在页面中搜索）．

引入：对于下面两个倍加矩阵

\[E_{12} = \begin{bmatrix} 1 & 0 & 0 \\ -5 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \quad E_{23} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -4 & 1 \\ \end{bmatrix} \]

有

\[{E_{12}}^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 5 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \quad {E_{23}}^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 4 & 1 \\ \end{bmatrix} \]

我们有

\[E_{23}E_{12} = \begin{bmatrix} 1 & 0 & 0 \\ -5 & 1 & 0 \\ 20 & -4 & 1 \end{bmatrix} \quad {E_{12}}^{-1}{E_{23}}^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 5 & 1 & 0 \\ 0 & 4 & 1 \end{bmatrix} \]

首先，所有的倍加操作都是左乘，因此右边的是第一步操作，左边的是第二步操作，操作顺序和乘积顺序是逆序的．同时，对两步操作整体求逆时，两步操作分别求逆后，操作的顺序也要逆序．这些都是必须注意的细节．

其次观察为什么前者的乘积，元素 \((1, 3)\) 是 \(20\)，而后者是 \(0\)．

原因是，当我们考虑对 \(A\) 先进行 \(E_{12}\) 变成 \(A'\)，再进行 \(E_{23}\) 变成 \(A''\)，\(E_{23}\) 用以倍加的第二行是 \(A'\) 的第二行，已经是新的，被第一行倍加影响过的第二行了，它不等同于 \(A\) 的第二行！因此两步操作的乘积作为 \(A''\) 相对于 \(A\) 变化的反映，第三行也要受到第一行的影响！

但是，当我们求逆后，先进行 \(E_{23}\)，再进行 \(E_{12}\)．你会发现第二步用以倍加的第一行从未被修改过，因此不会有这个多余的 \(20\)．

铺垫结束后我们来看 LU 分解．对于 \(A\)，假设我们可以进行若干 \(E\) 的操作后变为 \(U\)，而不需要做行置换，即无 \(P\)．可以记作

\[EA = U \]

\(E\) 是过程中用到的所有倍加矩阵的乘积，是一个下三角阵．对两侧左乘 \(L = E^{-1}\) 立即得

\[A = LU \]

即矩阵可以被分解为一个下三角和一个上三角的积．而 \(L\) 拥有性质：对于上面的引入，\(L\) 不会发生第一种情况，只会发生第二种情况，也就是倍加的顺序确保了每次用以倍加的行从未被修改过，保证 L 中的每个元素正好对应了所有先前倍加操作使用过的系数．

简单说明．Gauss 消元用到的顺序大概满足这样一个东西：

for (int i = 1; i <= n; ++i)
  for (int j = i + 1; j <= n; ++j)
    E_ij;

求逆后倒序是什么东西呢？

for (int i = n; i; --i)
  for (int j = n; j >= i + 1; --j)
    E_ij^-1;

可以显而易见得看到：用来倍加的行 \(i\) 在使用的时候，从未被修改过．

更进一步，\(L\) 是一个对角线为 \(1\) 的阵，而 \(U\) 不是．因此我们又有 \(A = LDU\) 分解，提出一个对角阵 \(D\) 后，让 \(U\) 也对角线归一．

LU 分解保前缀 \(0\) 性（别忘了讨论 LU 分解的前提是 Gauss 不涉及行置换）：

如果 \(A\) 的的第 \(i\) 行开头是连续的一段 \(0\)（这一段 \(0\) 长度不可在 \(i\) 以上，否则必须行置换），说明 \(L\) 的这一行开头也是连续的一段 \(0\)．这是因为这段前缀为 \(0\)，说明 来自上面的行（满足 \(j < i\) 的第 \(j\) 行）一定没有倍加到第 \(i\) 行过，因为第 \(j\) 行倍加到第 \(i\) 行的意义是消掉 \(a_{ij}\)，但这里 \(a_{ij} = 0\)．故 \(L_{ij}\) 作为第 \(i\) 行倍加到第 \(j\) 行的系数记录，值理应为 \(0\)．

如果 \(A\) 的第 \(i\) 列开头是连续的一段 \(0\)（同理长度不可在 \(i\) 以上），说明 \(U\) 的这一列开头也是连续的一段 \(0\)．这是因为来自上面的行（满足 \(j < i\) 的第 \(j\) 行）倍加到第 \(i\) 行也不影响这里第 \(i\) 列的值（因为都是 \(0\)）．

LU 分解在计算机科学中的意义是记忆化．考虑我们要存下了一个 \(A\)，然后随时会给一个 \(\bm b\)，要求我们求 \(A \bm x = \bm b\)．那么，我们可以考虑先将 \(A = LU\) 分解，根据上面的性质，\(L\) 保存了 Gauss 消元应当做的的全部操作记录．我们只需要将这些记录作用在 \(\bm b\) 上，就解得了方程

\[L\bm c = \bm b \]

接下来只需解 \(U \bm x = \bm c\)．\(U\) 是尊贵的上三角阵，因此简单回代或 Jordan 都是可以的．

转置

\[(AB)^\mathrm{T} = B^\mathrm{T}A^\mathrm{T} \]

经过矩阵乘法视角的洗礼，这个等式很容易感性理解正确性．矩阵乘法的左右乘其实就是行与列置换了一下的区别．

代 \(B = A^{-1}\)，得 \((A^\mathrm{T})(A^{-1})^\mathrm{T} = I\)，即

\[(A^\mathrm{T})^{-1} = (A^{-1})^\mathrm{T} \]

即，转置后求逆等于求逆后转置．

我们可以用这个记号表示向量点积：\(\bm x^\mathrm{T} \bm y\)．

转置有一个性质：对于任意向量 \(\bm x\) 和 \(\bm y\)，\(A \bm x\) 与 \(\bm y\) 的点积等于 \(\bm x\) 与 \(A^\mathrm T \bm y\) 的点积．

\[(A\bm x)^\mathrm{T} \bm y = \bm x^\mathrm{T}(A^\mathrm{T}\bm y) \]

称转置与自己相等的矩阵为对称矩阵，用 \(S\) 表示．

若 \(S\) 可逆，则 \(S\) 的逆一定对称．\(S\) 的逆的转置是 \(S\) 的转置的逆，即 \(S\) 的逆．

对于任意矩阵 \(A\)，我们有两种方法可以生成对称矩阵 \(S\)：\(A^\mathrm{T}A\)，\(AA^\mathrm{T}\)．

以 \(A^\mathrm{T}A\) 为例．\(A^\mathrm{T}A(i, j)\) 是 \(A^\mathrm{T}\) 的第 \(i\) 行与 \(A\) 的第 \(j\) 列点积，即 \(A\) 的第 \(i\) 列与第 \(j\) 列点积．两个列向量的点积显然具有交换律，故矩阵对称．

同时可以注意到，\(A^\mathrm{T}A\) 拥有非负的对角线（而且大概率是正的）．因为 \(A^\mathrm{T}(i, i)\) 是 \(A\) 第 \(i\) 列向量点积自己，非负且当且仅当列向量为 \(0\) 时为 \(0\)．

\(S\) 可以做 LU 分解．但真正保留对称性结构的是 LDU 分解，此时 \(U = L^\mathrm{T}\)，这称作 \(LDL^\mathrm{T}\) 分解．

\[S^\mathrm{T} = (L^\mathrm{T})^\mathrm{T}D^\mathrm{T}L^\mathrm{T} = LDL^\mathrm{T} \]

置换

对换矩阵 \(P_{ij}\) 是将 \(I\) 的第 \(i\)，\(j\) 行对换的结果．左乘对换行，右乘对换列，左行右列．是特殊的置换矩阵．

对换矩阵任意求积，可以凑出所有置换矩阵．置换矩阵是对 \(I\) 的任意行对换的结果．

置换矩阵是对称正交阵．\(P^\mathrm T P = I\)．

对换矩阵是对称正交阵的同时，还是对合矩阵，满足 \(P^2 = I\)，\(P^\mathrm T = P^{-1} = P\)．

考虑置换的 \(PA = LU\) 分解支持任意可逆阵．\(P = I\) 的朴素 \(LU\) 分解要求更高：\(A\) 的任一左上子方阵可逆，或称顺序主子式非零．

线性空间

线性空间和子空间

\(n\) 维实列向量构成的全体向量集合是一个线性空间 \(\R^n\)．另有其他线性空间，如 \(n\) 阶多项式线性空间 \(\mathbb P_n\)（次数 \(\le n\)．注意次数 \(=n\) 不可，最高次项被消去后不封闭），矩阵空间……

线性空间必须具有线性组合封闭性．注意：三维中的一个平面并不是 \(\R^2\)，而是 \(\R^3\) 的一个子空间．

子空间就是线性空间的一个必须满足封闭性的子集．

线性空间必须满足八条运算律．子空间直接继承线性空间的所有运算及运算律，故线性空间的运算律被验证后，无需进一步对子空间的运算律进行验证．八条运算律如下：

• \(\bm x + \bm y = \bm y + \bm x\)．
• \(\bm x + (\bm y + \bm z) = (\bm x + \bm y) + \bm z\)．
• 存在零元 \(\bm 0\)，对任意 \(\bm x\) 有 \(\bm x + 0 = \bm x\)．
• 对任意 \(\bm x\) 存在唯一 \(-\bm x\)，使得 \(\bm x + (-\bm x) = \bm 0\)．
• \(1 \bm x = \bm x\)．
• \((c_1c_2)\bm x = c_1(c_2 \bm x)\)．
• \(c(\bm x + \bm y) = c \bm x + c \bm y\)．
• \((c_1+c_2)\bm x = c_1 \bm x + c_2 \bm x\)．

前四条关于 \(\bm x + \bm y\)，5～6 关于 \(c \bm x\)，7～8 则是综合．

线性组合封闭性有一重要推论是线性空间必有零元．因为 \(0 \bm v\) 也是一种线性组合．

常见的线性空间反例：不经原点的空间结构；半平面 / 四分之一平面．封闭性是非常容易崩的．

对于一个线性空间 \(\bm V\) 的一个子集 \(S\)，因为 \(S\) 不一定封闭，它可能不是子空间．从 \(S\) 出发，将 \(S\) 内所有元素可以线性组合得到的全部元素也引入 \(S\)，构成集合 \(SS\)．则 \(SS\) 一定是 \(\bm V\) 的一个子空间，称其为 \(S\) 的生成子空间．

列空间

对于一个矩阵 \(A\)，列向量集合的生成子空间可以构成集合 \(\operatorname{Im}(A)\)，称作 \(A\) 的列空间．我们知道 \(A \bm x = \bm b\) 有一种线性组合的视角（列视角）．此时方程是否可解被转化为了一个判断 \(\bm b \in \operatorname{Im}(A)\) 的问题．

这里 \(\operatorname{Im}\) 是 Image 的缩写，中文是像．列空间也称作像空间，这是因为对于任意 \(n\) 维向量 \(\bm x\)，\(A \bm x\) 一定属于 \(\operatorname{Im}(A)\)，即列空间 / 像空间 的另一重要含义是 \(A\) 作为线性变换，可以作用得到的向量集，即

\[\operatorname{Im}(A) = \{\bm b \in \R^m \mid A \bm x = \bm b\} \]

零空间

设满足 \(A \bm x = \bm 0\) 的 \(\bm x\) 构成集合 \(\ker(A)\)．对于任意 \(\bm x_1, \bm x_2 \in \ker(A)\)，我们有 \(A \bm (\alpha \bm x_1 + \beta \bm x_2) = \bm 0\)，故 \(\alpha \bm x_1 + \beta \bm x_2 \in \ker(A)\)，这证明 \(\ker(A)\) 的线性组合封闭性，从而证明 \(\ker(A)\) 是 \(R^n\) 的一个子空间．我们称作 \(A\) 的零空间，或核空间（也记作 \(\ker A\)）．

类似列空间，零空间的另一含义是 \(A\) 作为线性变换，可以将其作用湮灭的向量集，即

\[\ker(A) = \{\bm x \in \R^n \mid A \bm x = \bm 0\} \]

如何求解 \(\ker(A)\)？

第一步：对矩阵 Gauss-Jordan 消元，得到 \(\mathbf{rref}(A)\)．\(A \to U \to R\)，在这个过程中 \(\ker(A) = \ker(U) = \ker(R)\) 保持不变．这里的 R 指的是 rref（reduced row echelon form,行简化阶梯形）．任何一个矩阵的 R 是唯一的，我们称作 \(\mathbf{rref}(A)\)．

rref 有以下特征：

• 主元列有 \(r\) 个，其中 \(r\) 是矩阵 \(A\) 的秩．下设主元列列编号分别为 \(c_1 < c_2 < \cdots < c_r\)．
• 对任意 \(1 \le i \le r\) 有 \(R(i, c_i) = 1\)；\(R(j \ne i, c_i) = 0\)．即，对于第 \(i\) 个主元列，只有第 \(i\) 行为 \(1\)，其余分量均为 \(0\)．
• 对任意 \(j < c_i\)，有 \(R(i, j) = 0\)．即，对于第 \(i\) 行，在第 \(c_i\) 列左侧的元素均为 \(0\)．
• 对任意 \(i > r\)，有 \(R(i, \cdots) = 0\)．即，第 \(r\) 行下方的行均为零行．

下面是一个 rref 的实例：

\[\begin{bmatrix} 1 & 0 & a & 0 & c \\ 0 & 1 & b & 0 & d \\ 0 & 0 & 0 & 1 & e \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} \]

第二步：初步分析 \(\ker(A)\) 的结构．如下：

• \(\ker(A)\) 是 \(\R^ m\) 的一个维数为 \(n - r\) 的子空间，即 \(\dim \ker(A) = n - r\)．这是因为 \(\dim \ker (A)\) 理应与自由变元数相同，它是 \(n - r\)．因此，\(\ker(A)\) 的表示方法应该是 \(n - r\) 个基向量的线性组合．
• 下称这 \(n - r\) 个基向量为基础解向量，这些基础解向量构成的集合称作基础解系．我们的目的就是找到一组基础解系．

第三步：构造合适的基础解系．

\(\mathbf{rref}(A)\) 会告诉我们 \(A\) 的 \(n - r\) 个自由变元是哪些，即除了 \(r\) 个主元列以外，剩下的列对应的主元．我们可以对这 \(n - r\) 个自由变元构造出 \(n - r\) 个基础解向量．

构造方式：充分利用自由变元的自由设定性，找到最简单的设定方法：第 \(i\) 个基础解向量是第 \(i\) 个自由变元为 \(1\)，其余自由变元均为 \(0\) 构成的解．还是以具体的 rref 为例：

\[\begin{bmatrix} 1 & 0 & a & 0 & c \\ 0 & 1 & b & 0 & d \\ 0 & 0 & 0 & 1 & e \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} \]

\(r = 3\)，\(n = 5\)．共有 \(x_3\) 和 \(x_5\)，\(n - r = 2\) 个自由变元，两个基础解向量分别为 \((-a, -b, 1, 0, 0)\) 与 \((-c, -d, 0, -e, 1)\)．于是，

\[\ker(A) = x_3 (-a, -b, 1, 0, 0) + x_5 (-c, -d, 0, -e, 1) \]

再来观察基础解向量的另一个含义．如特解 \((-a, -b, 1, 0, 0)\)，因为它是 \(A \bm x = \bm 0\) 的解，有

\[-a\bm{col(1)} -b\bm{col(2)} + \bm{col(3)} = \bm 0 \]

因此

\[\bm {col(3)} = a\bm{col(1)} + b \bm{col(2)} \]

因此，每个非主元列都可以表示为左侧所有主元列的线性组合．而基础解向量描述了这个线性组合的系数．值得注意的是这一点不仅在 rref 上成立，在原先的矩阵 \(A\) 上也成立，因为 Gauss-Jordan 变换不改变这一点的正确性．

最后研究一下 \(\ker(A)\) 的平凡性．\(\ker(A)\) 是平凡的（即仅零向量）当且仅当 \(r = n\)．\(\ker(A)\) 不平凡，当且仅当 \(r < n\)．

由于 \(r \le \min(n, m)\)，故 \(m < n\)，即方程数小于变元数时，\(\ker(A)\) 一定不平凡．

矩阵的秩

上面已经出现了矩阵的秩的概念．矩阵的秩 \(r\) 有以下几种等价的定义：

• \(r\) 是 \(A\) 的主元数量．
• \(r\) 是 \(A\) 的行向量最大线性无关数．
• \(r\) 是 \(A\) 的列向量最大线性无关数．
• \(r\) 是 \(\dim \operatorname{Im}(A) = \dim \operatorname{Im}(A^\mathrm T)\)．

另外

• \(n - r = \dim \ker (A)\)．

唯一 \(r = 0\) 的情形是全零阵．下面关注一下 \(r = 1\) 的矩阵．

\(r = 1\) 意味着 \(\dim \operatorname{Im}(A) = \dim \operatorname{Im}(A^\mathrm T) = 1\)，即 \(A\) 的行空间和列空间都是一条直线．\(\mathbf{rref}(A)\) 将只有一个非零行．

一个矩阵 \(A\) 是 \(r = 1\) 的，当且仅当其可表为两个向量的张量积，即 \(A = \bm u \bm v^\mathrm{T}\)．此时 \(A \bm x = \bm 0\) 即 \(\bm u(\bm v^\mathrm T \bm x) = \bm 0\)，即 \(\bm v \perp \bm x\)．说明此时 \(\ker(A)\) 是垂直于 \(\bm v\) 的一个 \(n - 1\) 维超平面．

矩阵的 CR 分解

任意 \(m \times n\) 的矩阵 \(A\) 可以被拆分为 \(m \times r\) 的矩阵 \(C\) 和 \(r \times n\) 的矩阵 \(R\) 的乘积，其中 \(C\) 是 \(A\) 的 \(r\) 个主元列，\(R\) 是 \(\mathbf{rref}(A)\) 的前 \(r\) 个非零行．

对 \(A = CR\) 的矩阵乘法使用张量积和视角，得到任意秩为 \(r\) 的矩阵可以分解为 \(r\) 个秩为 \(1\) 的矩阵之和．

Gauss-Jordan 消元的高观点

考虑 Gauss-Jordan 消元的过程．我们从左到右扫列，从上到下扫行．我们分别会回答这两个问题：

一列是否是先前的列的线性组合？

若答案是否，则这一列是主元列，说明这一列代表的变元是主元，而不是自由变元．rref 在这些主元列将表征为类似单位矩阵 \(I\) 的结构．

若答案是是，则这一列是自由变元列．rref 形式会告诉我们这一列将如何可表为先前列的线性组合（即线性组合的系数）．

一行是否是先前的行的线性组合？

若答案是是，则这一行包含主元．若答案是否，这一行会被转移到矩阵的下侧，并被消成零行．

事实上上面的扫描过程是 Gauss 的 \(A \to U\)．Jordan 的 \(U \to R\) 是又从下到上扫了一遍行．\(U\) 仅提供了哪些列不独立于先前的列的信息，而 \(R\) 进一步告诉我们不独立的列，表示为先前列的线性组合系数．

任意解

现在考虑解决 \(A \bm x = \bm b\)．需要注意的是，此时满足条件的 \(\bm x\) 不再构成线性空间，因为零元不存在．

步骤一：将 \(\bm b\) 增广到 \(A\) 右侧，\(\begin{bmatrix} A & \bm b \end{bmatrix}\)．然后对增广矩阵做 Gauss-Jordan．

这一步的目的是将 \(A\) 的倍加，置换操作等会同步到 \(\bm b\)，最后形成一个 \(R \bm x = \bm d\) 的形式，其中 \(R = \mathbf{rref}(A)\)．

步骤二：对 \(R \bm x = \bm d\) 找到一个特解．一个比较好的方法如下：

• 将自由变元全部设为 \(0\)．
• 将主元全部设为 \(d\) 的值．

如

\[R = \begin{bmatrix} 1 & 3 & 0 & 2 \\ 0 & 0 & 1 & 4 \\ 0 & 0 & 0 & 0 \end{bmatrix} \qquad \bm d = (1, 6, 0) \]

则 \(\bm x_p = (1, 0, 6, 0)\)．

步骤三：通解等于特解加齐次通解．所有解可以表示为特解与零空间的相加．因为

\[A(\bm x_p + \bm x_n) = A \bm x_p + A \bm x_n = \bm b \]

如这个例子中，\(\bm x_n = x_2(-3, 1, 0, 0) + x_4(-2, 0, -4, 1)\)，因此

\[\bm x = (1, 0, 6, 0) + x_2(-3, 1, 0, 0) + x_4(-2, 0, -4, 1) \]

值得一提的是，\(m = n = r\) 时，由于此时 \(\ker(A)\) 平凡，符合条件的解只有 \(\bm x_p\) 一个．而且，此时有

\[\bm x_p = A^{-1} \bm b \]

可解性测试

其实上面方程有解，还需要通过一个可解性测试：对于每个零行，\(\bm d\) 的对应坐标都必须是 \(0\)．否则，按照上述方法构造的特解也不能在非零行对应的方程处成立．这是方程有解的充要条件．

另外，假设可解性测试的结果构成布尔函数 \(\varphi(\bm d)\)，则

\[\operatorname{Im}(A) = \{\bm b \in \R^m \mid \varphi(\bm b)\} \]

即可解性测试结果为真的全部向量构成 \(A\) 的列空间．这提供了描述列空间的另一视角，我们可以用可解性测试得到的约束方程直接描述列空间．下面是例子．

\[\begin{bmatrix} 1 & 2 & 3 & 5 \\ 2 & 4 & 8 & 12 \\ 3 & 6 & 7 & 13 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} \]

对增广阵进行 Gauss 消元，可以化为

\[\left[ \begin{array}{cccc|l} 1 & 2 & 3 & 5 & b_1 \\ 0 & 0 & 2 & 2 & b_2 - 2b_1 \\ 0 & 0 & 0 & 0 & b_3 + b_2 - 5b_1 \end{array} \right] \]

可解性测试要求 \(b_3 + b_2 - 5b_1 = 0\)．故这个方程可以直接描述列空间：

\[ \operatorname{Im}(A) = \{\bm b \in \R^3 \mid b_3 + b_2 - 5b_1 = 0\} \]

解空间与矩阵形态

列满秩矩阵（矮胖）：\(r = n \le m\)．对于这样的 \(A\)，其 rref 一定是这样的一个形式：

\[\begin{bmatrix} I \\ 0 \end{bmatrix} \]

列满秩矩阵在向量视角的特点是：列向量线性无关．

列满秩矩阵在方程组视角的特点是：无自由变元，因此 \(\ker(A)\) 一定平凡．故其最多只有一个解．

有解当且仅当 \(\bm d\) 在非零行的坐标均为 \(0\)，这一点后续将不再强调．

行满秩矩阵：\(r = m \le n\)（瘦高）．

行满秩矩阵在向量视角的特点是：行向量线性无关．

行满秩矩阵在方程视角的特点是：无零行，因此方程一定有解．\(\ker(A)\) 的维数是 \(n - r = n - m\)．

经过上面的讨论，我们可以进一步将矩阵分为四类．同时可以表示四种矩阵的 \(R\)．为了方便表示，此时我们假设主元列在连续的开头（显然交换列本质只改变变元序号）．

• \(r = m = n\)：可逆方阵．此时 \(A \bm x = \bm b\) 一定有 \(1\) 个解．\(R = [I]\)．
• \(r = m\) 且 \(r < n\)：行满秩非方阵矩阵（胖）．此时 \(A \bm x = \bm b\) 一定有 \(\infty\) 个解．\(R = \begin{bmatrix}I & F\end{bmatrix}\)．
• \(r = n\) 且 \(r < m\)：列满秩非方阵矩阵（瘦）．此时 \(A \bm x = \bm b\) 一定有 \(0\) 或 \(1\) 个解．\(R = \begin{bmatrix}I \\ 0\end{bmatrix}\)．
• \(r < n\) 且 \(r < m\)：不满秩矩阵．此时 \(A \bm x = \bm b\) 一定有 \(0\) 或 \(\infty\) 个解．\(R = \begin{bmatrix}I & F \\ 0 & 0\end{bmatrix}\)．

线性无关、基、维数

一组向量线性无关的两种表述：

• 一个向量无法表示为其它向量的线性组合．
• 上面的「一个向量」，量词是存在还是任意是不重要的，因为是等价的．
• 所有向量线性组合出 \(\bm 0\) 的情况只有所有向量的系数均为 \(0\)．

下面这个表述没有特殊化任何一个向量，表述上拥有对称性．更常用于判断向量组的线性无关性．上面这个表述常用作线性无关性的性质．

值得注意的是，若一个向量组内有零向量，可立即确定向量组线性相关．故对于平凡空间，其基不是零向量，而是空集．

现在是时候给出维数的标准定义了，其实我们早就已经准备好．

线性空间的一组基：一个向量组，同时满足两个条件：

• 足够多（可张成性）：该向量组足以张成（span）这个线性空间．
• 足够少（线性无关性）：该向量组线性无关．

一个线性空间可能有多组基，但每一组基有相同的大小．证明如下：

假设一个线性空间有两组大小不同的基，不妨设其一为 \(\bm v_1, \bm v_2, \ldots, \bm v_m\)，另一为 \(\bm w_1, \bm w_2, \ldots, \bm w_n\)，且其中 \(n > m\)．

因为基张成了整个线性空间，任何一个 \(\bm w\) 可以由 \(\bm v\) 线性表出．则

\[W = \begin{bmatrix} \bm w_1 & \bm w_2 & \ldots & \bm w_n \end{bmatrix} = \begin{bmatrix} \bm v_1 & \bm v_2 & \ldots & \bm v_m \end{bmatrix} \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix} = VA \]

\(A\) 是一个 \(n > m\) 的矮胖形矩阵，可得 \(A \bm x = \bm 0\) 有非零解．这意味着 \(VA \bm x = \bm 0\) 也有非零解，即 \(W \bm x = \bm 0\) 有非零解．这意味着 \(W\) 线性相关，与 \(W\) 是基矛盾．证毕．

因为每一组基有相同的大小，称其大小为线性空间的维数．本质上是线性空间的自由度．

对于一组基，线性空间的任意一个向量用这个基表出的线性系数组合唯一．证明是假设

\[\bm v = a_1\bm v_1 + a_2 \bm v_2 + \cdots + a_n \bm v_n = b_1 \bm v_1 + b_2 \bm v_2 + \cdots + b_n \bm v_n \]

则

\[(a_1 - b_1)\bm v_1 + (a_2 - b_2) \bm v_2 + \cdots + (a_n - b_n) \bm v_n = \bm 0 \]

由基 \(\bm v\) 的线性无关性可知，\(a_i - b_i = 0\)，故 \(a_i = b_i\)，这就证明了系数的组合是唯一的．

如果一个向量组的大小等于线性空间的维数，则可张成性和线性无关性证一即可证向量组基．换言之，数目正确，可张成性，线性无关，三者知二立证向量组是基（同时得到另一性质）．

矩阵 \(A\) 的 \(r\) 个主元列构成 \(\operatorname{Im}(A)\) 的一个基．需要注意一个易错点：

虽然主元列的编号一般要通过 \(R\) 得到，但这里代的是 \(A\) 的主元列，而不是 \(U\) 或者 \(R\) 的．Gauss-Jordan 操作涉及很多行置换操作和行倍加操作，这不影响的是行空间和零空间，即 \(\operatorname{Im}(A^\mathrm T) = \operatorname{Im}(R^\mathrm T)\)，\(\ker(A^\mathrm T) = \ker(R^\mathrm T)\)．然而，它是会影响列空间的，因为列向量本身发生了非线性组合变换．

矩阵 \(A\) 的大小为 \(n - r\) 的基础解系构成 \(\ker(A)\) 的一个基．

若 \(\bm v_1, \bm v_2, \ldots, \bm v_n\) 是 \(\R^n\) 的一个基，则对于任意不可逆矩阵 \(A\)，\(A\bm v_1, A\bm v_2, \ldots, A\bm v_n\) 也是 \(\R^n\) 的一个基．这一点有点线性变换的意思，我们会在线性变换一章进一步讨论这个性质．

最后我想厘清一个非常重要的逻辑问题．向量本身与基无关，但写向量的坐标，分量形式的时候，就已经依赖于一组基的选取了．

前半句很明显，无论选取的基如何，任何一个向量 \(\bm v\) 就在那里，不会随着选取的基而变化．但是，只要当我们写出 \(\bm v = (v_1, v_2, \ldots, v_n)\) 这种分量形式的时候，就已必须依赖一组选取的基了．

厘清这一点很重要，只是先前的表述中，为了描述清概念，我们一直忽略这一点——我们默认随便选取了一组标准正交基上讨论问题．但是，即使是标准正交基也并不唯一，一个 \(n \ge 2\) 的子空间就可以有无数组标准正交基，用不同的基刻画同一向量，刻画出的坐标分量形式往往截然不同．

标准的含义是向量模长为 \(1\)．下面不再重述此概念的定义．

非向量线性空间初步

矩阵空间．对于 \(n \times n\) 的矩阵构成的空间，其维数为 \(n^2\)．如 \(2 \times 2\) 的矩阵维数是 \(4\)，其中最简单的一组基是

\[\left( \begin{bmatrix}1 & 0 \\ 0 & 0\end{bmatrix}, \begin{bmatrix}0 & 1 \\ 0 & 0\end{bmatrix}, \begin{bmatrix}0 & 0 \\ 1 & 0\end{bmatrix}, \begin{bmatrix}0 & 0 \\ 0 & 1\end{bmatrix} \right) \]

进一步地可以讨论这个矩阵空间的子空间：

• 对称矩阵 \(S\) 构成的子空间维数为 \(\dfrac {n(n+1)} 2\)．对于每个 \((i, j)\) 构成的无序二元对，构造矩阵 \(a_{ij} = a_{ji} = 1\)，其余为 \(0\)．这些矩阵构成基．
• 对角矩阵 \(D\) 构成的子空间维数为 \(n\)．
• 上三角矩阵 \(U\) 构成的子空间维数同 \(S\)．

函数空间．我们讨论一个齐次线性微分方程的问题．形如

\[a_ny^{(n)}x + a_{n-1}y^{(n-1)} + \cdots + a_2y'' + a_1y' + a_0y = 0 \]

的方程称作齐次线性微分方程，出现过的最高阶的导数是方程的阶．下面证明：

• 齐次线性微分方程构成的所有解，形成函数空间 \(\bm F\) 的一个线性子空间．
• 该线性子空间的维数等于方程的阶数 \(n\)．

第一点的证明考虑解的线性封闭性即可．对符合齐次线性微分方程的两个函数 \(y_1\) 和 \(y_2\)，可以发现 \(\alpha y_1 + \beta y_2\) 同样符合该方程，得证．

第二点的证明，考虑构造线性空间的一组基．

首先．我们知道，微分方程的解可以由初始条件唯一确定．而 \(n\) 阶微分方程，初始条件的自由度是 \(n\)．当我们知道 \(y(0)\)，\(y'(0)\)，\(y''(0)\)，……，\(y^{n-1}(0)\) 的值时：

• \(y^n(0)\) 的值由方程得出．
• 接下来所有的 \(y(x)\) 的信息也因为方程的规约均可知．整个函数被唯一确定了．

而初始条件不同，求出的函数解必然不同（相同的函数解初始条件必须吻合）．因此，对于有 \(n\) 个自由度的初始条件，直接分别令每个初始条件为 \(1\)，其余为 \(0\)，即可得到 \(n\) 个线性无关的解．如

• 解 \(y_0\) 满足 \(y(0) = 1\)，\(y^{(k)}(0) = 0\)，\(k \ne 0\)．
• 解 \(y_1\) 满足 \(y'(0) = 1\)，\(y^{(k)}(0) = 0\)，\(k \ne 1\)．
• 解 \(y_2\) 满足 \(y''(0) = 1\)，\(y^{(k)}(0) = 0\)，\(k \ne 2\)．
• ……
• 解 \(y_{n - 1}\) 满足 \(y^{n - 1}(0) = 1\)，\(y^{(k)}(0) = 0\)，\(k \ne n - 1\)．
• 上面的所有 \(k\) 有宏观约束范围 \(0 \le k \le n - 1\)．

假设我们现在要一个解 \(Y\) 满足 \(Y(0) = 5\)，\(Y'(0) = 3\)，……，我们可以直接令

\[Y = 5y_0 + 3y_1 + \cdots \]

则 \(Y\) 就是满足条件的解．同时我们自然证明了 \(Y = 0\) 及线性组合方式是全零系数．这就同时证明了这组基的任意可表性和线性无关性．

对于非齐次线性微分方程，其解的形态也与先前的理论不谋而合．仍然是一个特解 + 零空间的形式．如 \(y'' = 2\)，其解为 \(y = x^2 + cx + d\)．其中 \(x^2\) 是特解，\(cx + d\) 是零空间．

四子空间维数论

矩阵 \(A\) 的秩 \(r\) 之所以重要，是因为其刻画了 \(A\) 的四个子空间的维数．如下：

• 列空间：\(\operatorname{Im}(A)\)：\(\R^m\) 的一个维数为 \(r\) 的子空间．
• 行空间：\(\operatorname{Im}(A^\mathrm{T})\)：\(\R^n\) 的一个维数为 \(r\) 的子空间．
• 零空间：\(\ker(A)\)：\(\R^n\) 的一个维数为 \(n - r\) 的子空间．
• 左零空间：\(\ker(A^\mathrm{T})\)：\(\R^m\) 的一个维数为 \(m - r\) 的子空间．

研究 \(A\) 的这些空间，最好的方式是考虑 rref \(R\)．\(R\) 的四子空间维数与 \(A\) 均保持相同，而其中的两个子空间完全保持不变，分别是行空间和零空间．

以下面这个 rref 为例，分别研究四个子空间．

\[R = \begin{bmatrix} 1 & 3 & 5 & 0 & 7 \\ 0 & 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} \]

行空间．对于 rref，\(r\) 个非零行向量构成 \(\operatorname{Im}(R^\mathrm{T})\) 的一个基，简单说明如下：

• 一方面，零行一定不是基的一部分，对 \(\operatorname{Im}(R^\mathrm{T})\) 无贡献．
• 另一方面，非零行中，若将主元列单独取出，会形成一个 \(r \times r\) 的单位矩阵 \(I\)．这可以证明这 \(r\) 个行向量是线性无关的．

列空间．对于 rref，主元列向量是 \(\operatorname{Im}(R)\) 的一个基．简单说明如下：

• 若将主元列向量取前 \(r\) 个分量（剩余截断），同样形成一个 \(r \times r\) 的单位矩阵 \(I\)，说明线性无关性．
• 另一方面，非主元列根据 rref 的结构，一定可以表示为先前主元列的线性组合（这就是基础解向量！）．

零空间．\(n - r\) 个自由主元，就是 \(n - r\) 个自由度，就是 \(n - r\) 的维数．

更具体而言，\(n - r\) 个基础解向量中，每一个向量都有一个元，只有它为 \(1\) 而其他向量的该元都为 \(0\)．所以这本质上也类似单位矩阵 \(I\) 刻画出的线性无关性．

左零空间．左零空间是先前没有提到过的一个子空间．其寻求的是行向量线性组合为 \(\bm 0^\mathrm{T}\) 的方案．

考虑 \(\ker(R^\mathrm{T})\) 时，这个问题是比较简单的．由于 \(R\) 的前 \(r\) 行是线性无关的，而剩下的 \(m - r\) 行均为零行．因此，将这些行组合成零向量，唯一可能系数的方案是

\[(0, 0, \ldots, 0, y_1, y_2, \ldots, y_{m - r}) \]

其中 \(0\) 有 \(r\) 个，\(y\) 可以任意取值．

这个系数组合方案有 \(m - r\) 个自由度，所以 \(R\) 的左零空间维数是 \(m - r\)．

上面讨论并说明了 \(R\) 的四子空间维数．下面应该说明 \(A\) 的四子空间维数为何对应相等．

首先，\(A\) 和 \(R\) 的行空间和零空间完全一致．前者是因为行倍加和行置换只是对行向量进行一些线性组合的修改操作，后者是因为 Gauss-Jordan 不改变方程的等价性．故 \(A\) 的行空间和零空间的维数自然分析完成．

但是，\(A\) 和 \(R\) 的列空间、左零空间通常不相同．它们只是维数相同，这需要证明．

首先是列空间．\(\dim \operatorname{Im}(A) = \dim \operatorname{Im}(R)\)．这是因为，\(R\) 和 \(A\) 虽然列空间不同，但列向量的线性相关性（以及对应的系数组合）都完全相同．比如，若在 \(R\) 中，第四列向量是三倍的第一列加上四倍的第三列，则在 \(A\) 中同样有第四列是三倍的第一列加上四倍的第三列．\(R\) 中直观的体现线性组合信息（用基础解向量刻画的），对 \(A\) 同样适用．

因此我们证明了：

对于 \(n\) 个维数的 \(\R^n\)，其两个子空间，行空间的维数 \(r\) 与零空间的维数 \(n - r\) 相加必得 \(n\)．

事实上，对于任意矩阵 \(A\)，只需对 \(A^\mathrm{T}\) 运用上面的定理，立即得

对于 \(m\) 个维数的 \(\R^m\)，其两个子空间，列空间的维数 \(r\) 与左零空间的维数 \(m - r\) 相加必得 \(m\)．

\(A\) 的左零空间维数是 \(m - r\) 可以如此证明．为了更好的探究左零空间的本质，下面指出一个性质：

考虑从 \(A\) 经过一系列初等行变换 \(E\) Gauss-Jordan 成 \(R\) 的过程，\(EA = R\)．则，\(E\) 的最后 \(m - r\) 行行向量，正是 \(A\) 左零空间的基．

这是为何？首先 \(E\) 是变换形成的矩阵，所以它可逆．因此，\(E\) 的最后 \(m - r\) 行行向量线性无关．

同时，\(E\) 的最后 \(m - r\) 行行向量左乘 \(A\) 的结果是 \(R\) 的最后 \(m - r\) 个零行，所以它们属于左零空间．因此，这 \(m - r\) 个向量张成了左零空间（因为数量已经与维数 \(m - r\) 相等）．

矩阵的等价

\(r(AB) \le r(A)\)，且 \(r(AB) \le r(B)\)．一个矩阵左乘，右乘任意矩阵，秩单调不增．

形象言之，秩理解为秩序，矩阵乘法只能让秩序只能变小或不变，不能变大．其实这种形象的理解也有一定道理，因为秩刻画的是线性无关性．线性无关相对线性有关是更宝贵的性质．

以 \(r(AB) \le r(A)\) 为例．采用左乘变换视角，\(AB\) 将 \(B\) 的列空间进行 \(A\) 的变换，变换到 \(A\) 的列空间内部．故一定有 \(r(AB) \le r(A)\)．同理得 \(r(AB) \le r(B)\)．

这可以引入另一性质．对于可逆矩阵 \(K\)，则 \(r(KA) = r(AK) = r(A)\)．这是因为

\[r(A) = r(AKK^{-1}) \le r(AK) \le r(A) \]

换句话说，\(A\) 左乘 \(K\) 再左乘 \(K^{-1}\) 后仍是 \(A\)，起点与终点的秩相同，而乘的过程秩不增，因此秩只能不变．换言之，如果乘一个矩阵降秩，则乘这个矩阵的操作不可能可逆．

这里引出矩阵等价的概念．定义两个同型矩阵 \(A \cong B\)，当且仅当存在可逆阵 \(P\)，\(Q\) 满足 \(B = PAQ\)．

由上面的性质，这等价于 \(r(A) = r(B)\)．即同型矩阵，秩相同即等价．不变量是秩．

任一可逆阵可以分解为有限个初等变换的积．这是因为可逆阵 \(P\) 可以 Gauss-Jordan 为 \(I\)，这中间涉及的操作均为初等行变换．初等变换包括三种，倍加，置换，数乘，前两种不改 \(\det\)，最后一种 \(\det\) 乘对应的数字．

因此，\(A \cong B\) 同样等价于经初等变换可互达．将 \(P\) 和 \(Q\) 拆成初等变换的积，\(P\) 对应初等行变换，\(Q\) 对应初等列变换．

正交性

四子空间正交论

两个向量正交，当且仅当 \(\bm v^\mathrm{T} \bm w = 0\)．此时，勾股定理指出

\[\| \bm v \|^2 + \| \bm w \|^2 = \| \bm v + \bm w \|^2 \]

也可以用在 \(\bm v^\mathrm{T} \bm w = \bm w^\mathrm{T} \bm v = 0\) 时，有

\[(\bm v + \bm w)^\mathrm{T} (\bm v + \bm w) = \bm v^\mathrm{T} \bm v + \bm w^\mathrm{T} \bm w \]

来解释．

两个子空间正交：\(\bm V\) 与 \(\bm W\) 正交，当且仅当对任意 \(\bm v \in \bm V\)，\(\bm w \in \bm W\)，有 \(v\) 与 \(w\) 正交．

一个面和垂直于它的线是正交的．两个垂直的面并不正交，因为垂直的平面并不满足两平面内任意直线对垂直．

若 \(\bm V\) 与 \(\bm W\) 正交，且 \(\bm v \in \bm V\)，\(\bm v \in \bm W\)，则一定有 \(\bm v = \bm 0\)．

四子空间正交论一：矩阵 \(A\) 的 \(\ker(A)\) 与 \(\operatorname{Im}(A^\mathrm{T})\)，是 \(\R^n\) 内的两个正交子空间．

原因是考虑 \(\ker(A)\) 的定义：

\[A \bm x = \bm 0 \]

根据行视角，这相当于 \(\bm x\) 与 \(A\) 的每一行点积，结果均为 \(0\)．这些行向量，包含了 \(\operatorname{Im}(A^\mathrm{T})\) 的一组基．

四子空间正交论二：矩阵 \(A\) 的 \(\ker(A^\mathrm{T})\) 与 \(\operatorname{Im}(A)\)，是 \(\R^m\) 内的两个正交子空间．注意左零空间的定义应为

\[\bm x^\mathrm{T} A = \bm 0 \]

对上式两侧转置，则 \(\bm x\) 点积的对象是 \(A^\mathrm T\) 的行向量，即 \(A\) 的列向量．

事实上四子空间的性质比单纯的正交还要强．考虑 \(\R^3\) 的立体空间中，两条直线也是可以正交的，但是它们的维数和 \(2 \ne 3\)．四子空间不可以如此．

正交补：对于子空间 \(\bm V\)，其正交补 \(\bm V^\perp\) 定义为所有与 \(\bm V\) 正交的向量构成的子空间．

上面提到的两对正交的子空间，事实上它们是正交补的关系．即

\[\ker(A)^\perp = \operatorname{Im}(A^\mathrm{T}) \\ \ker(A^\mathrm{T})^\perp = \operatorname{Im}(A) \]

这就是四子空间正交论的核心，非常美丽而深刻．我们应当用自然语言重新梳理这个逻辑：零空间中的任意元素 \(\bm x\) 作为 \(A \bm x = 0\) 的解，维数与行向量相同，均为 \(\R^n\) 中的元素．但是，它却与每个行向量正交了，故其不仅不在行空间中，还恰好与行空间正交．进一步地，零空间作为所有这样的 \(\bm x\) 的集合，完整精确地刻画了与行空间正交的所有向量，正好不缺漏地构造了在整个 \(\R^n\) 中，与行空间完全对立的阵营，只不过这里对立是一种比喻的说法，正确的描述是正交．于是，行空间与零空间构成 \(\R^n\) 的一对正交补．

正交分解：对于任意向量 \(\bm x\) 和一对正交补，如 \(\ker(A)\) 与 \(\operatorname{Im}(A^\mathrm{T})\)，其有且仅有一种正交分解方式 \(\bm x = \bm x_r + \bm x_n\)，满足 \(\bm x_r \in \operatorname{Im}(A^\mathrm{T})\) 且 \(\bm x_n \in \ker(A)\)．

于是，

\[A \bm x = A(\bm x_r + \bm x_n) = A \bm x_r + A \bm x_n = A \bm x_r + \bm 0 = \bm b \]

即，

• 核空间分量被湮灭：\(A\bm x_n = \bm 0\)．
• 行空间分量变为列向量：\(A \bm x_r = \bm b\)．

我们惊喜地发现：\(A \bm x = \bm b\) 中，原来 \(\bm x\) 在零空间的分量被湮灭，在行空间的分量提供全部的变换结果，同时，变换结果还属于列空间．这个式子居然同时涉及三个空间．至于左零空间，其则是 \(A \bm x\) 的结果永远不可达之处．它没有收集到所有不可达的向量，它的信息是：如果一个向量 \(\bm b\) 有左零空间的分量，则 \(A \bm x\) 一定不可达 \(\bm b\)．

让我们来迎接全球最美图片．

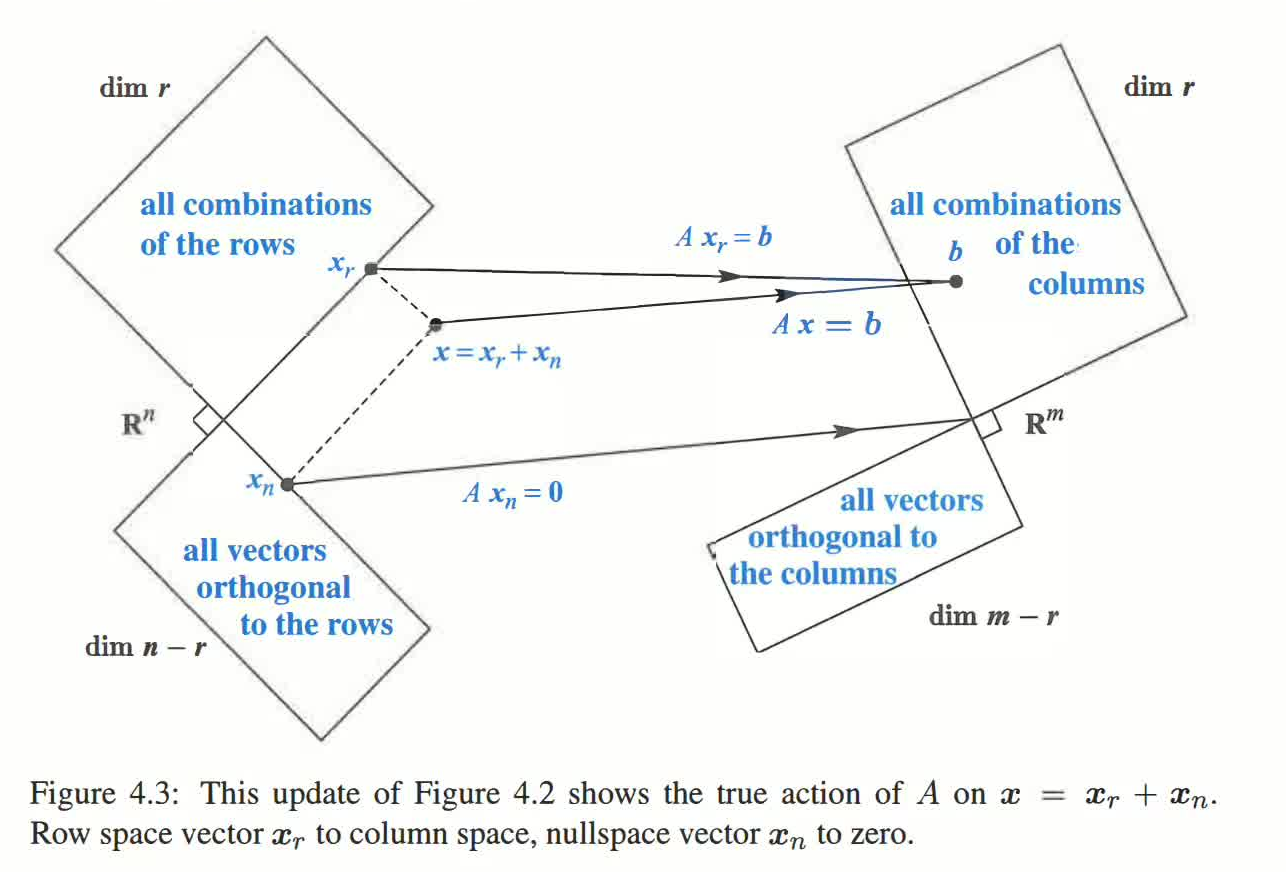
更进一步，如果 \(A \bm x_r = A \bm x_r'\)，则 \(A \bm (x_r - x_r') = \bm 0\)，故 \(x_r - x_r' \in \operatorname{Im}(A^\mathrm{T}) \cup \ker(A) = \{\bm 0\}\)．这里用到的性质很重要，需要再次强调．若一个向量同时在正交的两个子空间中，则该向量必为零向量．因为，正交于自己的向量必为零向量．

这说明什么？对于任意 \(\bm b \in \operatorname{Im}(A)\)，有且仅有一个 \(\bm x_r \in \operatorname{Im}(A^\mathrm T)\) 满足 \(A \bm x_r = \bm b\)．\(A\) 的列空间与行空间在 \(A\) 本身对应的线性变换下构成双射．此二者可以构成双射是不奇怪的，因为二者是维数相同的子空间，但 \(A\) 本身就是一个双射桥梁，还是十分令人惊奇的发现．

当然，双射意味着可逆，故将行空间变换到列空间的这一部分 \(A\) 必有它的逆．这一部分的逆的信息将会蕴含在伪逆（pseudoinverse）\(A^+\) 中，后面展开．

投影

上面的正交分解用到了投影这个操作．正交分解出的分量，是向量投影到子空间的结果．投影分为正交投影和斜投影．我们一般只讨论前者．

以 \(\R^3\) 中的向量 \(\bm p = (x, y, z)\) 投影为例．我们可以将它投影到两个互为正交补的子空间：\(z\) 轴与 \(xOy\) 平面．投影的结果应分别是 \(\bm p_1 = (0, 0, z)\)，\(\bm p_2 = (x, y, 0)\)．

这个操作是一种线性变换，可以刻画为矩阵．具体而言：

\[P_1 = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}, P_2 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} \]

则 \(\bm p_1 = P_1 \bm b\)，\(\bm p_2 = P_2 \bm b\)．

因为两次投影到的子空间是正交补的，投影结果和投影矩阵也成补的关系：

• \(\bm p_1 + \bm p_2 = \bm b\)．
• \(P_1 + P_2 = I\)．

另外，一切投影矩阵 \(P\) 还满足两个美丽性质：

• \(P^2 = P\)，即幂等矩阵．含义是两次投影与一次投影等效．事实上这是投影的标准定义（包括斜投影），但是通常讨论的正交投影是其子集，故通常讨论的投影矩阵也是幂等矩阵的子集．
• \(I - P\) 也是投影矩阵．考虑 \((I - P)\bm b = \bm b - P \bm b\)．当 \(P\) 将 \(\bm b\) 投影到一个子空间 \(\bm V\)，则 \(I - P\) 会将 \(\bm b\) 投影到正交补 \(\bm V^\perp\)．

下面研究投影到 \(\R^m\) 的任意子空间的情形．首先我们应为子空间选取一组基．对于子空间 \(\bm V\)，我们考虑将它的一组基以列向量形式组合成矩阵 \(A\)，现在只需研究任意向量 \(\bm b\) 到投影到 \(A\) 上的向量 \(\bm p\)（这里我们定义出投影到矩阵的概念——实质是投影到矩阵列向量张成的子空间），以及对应的投影变换矩阵 \(P\)．

不知读者有没有注意到这里的微妙点．上面的操作往往蕴含了两层基．我们选取 \(\bm V\) 的 \(\dim V\) 个线性无关向量作为 \(\bm V\) 的一组基 \(\alpha\)，列为矩阵 \(A\)；但同时，这些线性无关的向量本身也已应当用坐标形式展出，因为我们需要展示成矩阵，而向量本身用坐标形式展示就已经依赖于一组基 \(e\) 了．

上面出现了两组基 \(\alpha\) 和 \(e\)．\(\alpha\) 是我们对 \(\bm V\) 找到的一组基，大小为 \(\dim V\)，每个向量维数为 \(m\)．而 \(e\) 是更为本质的全局标准正交基，通常不会显式地给出．这组基通常用来全局地表示所有向量的坐标，而且基本都是标准正交基（否则问题会变得复杂）．

从理论的角度，我们对 \(e\) 和 \(\alpha\) 的选取是任意的：

• \(e\) 和 \(\alpha\) 选取结果均不影响投影向量本身，因为基不影响向量本身．
• \(e\) 的选取会影响投影向量的坐标表示（因为它直接影响投影向量如何表达）．
• 在 \(e\) 确定时，\(\alpha\) 的选取结果不会影响投影向量的坐标表示，因为它其确定出的投影空间 \(\bm V\) 始终是确定的．

从做题的角度，题目通常会默认给出一些向量的坐标，这个时候已经确定下 \(e\) 了，故 \(e\) 通常在做题中是继承题面而非我们自己选取，自己操作的通常是 \(\alpha\)．

重申 \(P\) 的效果．\(P\) 会将 \(\bm b\) 投影到 \(\bm V\)，且刚才我们用矩阵将 \(\bm V\) 转化为 \(\operatorname{Im}(A)\)．那么 \(I - P\) 将会把 \(\bm b\) 投影到哪？答案是 \(A\) 的左零空间 \(\ker(A^\mathrm T)\)，因为左零空间和列空间是一对正交补．

先研究 \(n = 1\) 的情形，即子空间是一维的，矩阵是一个列向量 \(\bm a\)．

此时，\(\bm b\) 在 \(\bm a\) 上的投影 \(\bm p\) 一定是 \(\bm a\) 的一个数乘．我们称这个系数为 \(\hat x\)：

\[\bm p = \hat x \bm a \]

只要我们得到了 \(\hat x\)，就得到了 \(\vec p\)，最终就可以解出 \(P\)．下面所有投影方式都是这个研究顺序．

设 \(\bm e = \bm b - \bm p = \bm b - \hat x \bm a\)，则 \(\bm e \perp \bm a\)．我们是用这个正交信息确定 \(\hat x\) 的．具体而言，

\[\bm a \cdot (\bm b - \hat x \bm a) = 0 \implies \hat x = \dfrac{\bm a \cdot \bm b}{\bm a \cdot \bm a} = \dfrac{\bm a^\mathrm T \bm b}{\bm a^\mathrm T \bm a} \]

即

\[\bm p = \bm a \hat x = \bm a \dfrac{\bm a ^ \mathrm T \bm b}{\bm a ^ \mathrm T \bm a} = P \bm b \]

其中

\[P = \dfrac{\bm a \bm a^\mathrm T}{\bm a^\mathrm T\bm a} \]

由于 \(P\) 的分子是一个张量积的形式，因此 \(r(P) = 1 = \dim \bm V\)．这一点很合理，因为 \(P\) 的列空间就是在刻画 \(P \bm x\) 的可达之处，其正是投影空间．故 \(r(P)\) 作为列空间的维数 \(\dim \operatorname{Im}(P)\)，理应为 \(\dim \bm V = 1\)．

可以自行验证 \(P^2 = P\) 与 \(I - P\) 是否将 \(\bm b\) 成功投影到 \(\bm e\)．

现在考虑任意 \(n \times m\) 的矩阵 \(A\)，对应 \(n\) 个在 \(\R^m\) 中的线性无关的向量 \(\bm a_1, \ldots, \bm a_n\)．

对于任意 \(\bm b\)，我们想要找到 \(\operatorname{Im}(A)\) 中的一个向量 \(\bm p\) 作为投影．这样的向量可以表示为

\[\bm p = A \bm {\hat x} \]

此时 \(\bm {\hat x}\) 变成了一个向量．确定它的方式仍然是正交：\(\bm a_i \cdot (\bm b - A \bm {\hat x}) = 0\)．

将上面这 \(n\) 个限制刻画为矩阵的形式，可以得到

\[A^\mathrm T(\bm b - A \bm {\hat x}) = \bm 0 \]

其中 \(A^\mathrm T\) 的第 \(i\) 个行向量正是 \(A\) 的第 \(i\) 个列向量 \(\bm a_i\) 的转置．所以上面这个刻画是相当直观的．

事实上这个式子还有另一巧妙的理解．\(\bm b - A \bm {\hat x}\) 正是 \(\bm b\) 的另一投影分量——在 \(\operatorname{Im}(A)^\perp = \ker(A^\mathrm T)\) 上的投影分量．上式正是在刻画这个向量属于 \(A\) 的左零空间．

下面需用线性代数的运算律处理此式．

\[A^\mathrm T(\bm b - A \bm {\hat x}) = \bm 0 \iff A^\mathrm TA \bm {\hat x} = A^\mathrm T\bm b \]

这里出现了一个矩阵：\(A^\mathrm TA\)．这是一个 \(n\) 阶对称方阵．

一个性质：\(A\) 的列向量线性无关可以推得 \(A^\mathrm T A\) 是可逆的．因此，

\[\bm {\hat x} = (A^\mathrm TA)^{-1} A^\mathrm T\bm b \]

于是

\[\bm p = A \bm {\hat x} = A(A^\mathrm TA)^{-1} A^\mathrm T \bm b = P \bm b \]

其中

\[P = A(A^\mathrm TA)^{-1} A^\mathrm T \]

上面用到的一个性质很重要，需要证明：

\(A\) 的列向量线性无关可以推得 \(A^\mathrm T A\) 是可逆的．

事实上我们有一个更强的结论：

\[\ker(A ^ \mathrm T A) = \ker(A) \]

结论详细含义在半正定矩阵讨论．证明了这个结论，则 \(A\) 的列向量线性无关即 \(\ker(A)\) 平凡，能直接推得方阵 \(\ker(A ^ \mathrm TA)\) 也是平凡的，进而直接证明 \(A ^ \mathrm TA\) 的可逆性．

\[A\bm x = \bm 0 \implies A ^ \mathrm TA \bm x = \bm 0 \]

同时，

\[A ^ \mathrm TA \bm x = \bm 0 \implies \bm x ^ \mathrm TA ^ \mathrm TA \bm x = 0 \implies (A\bm x) ^ \mathrm T(A \bm x) = 0 \implies \|A \bm x\| = 0 \implies A \bm x = \bm 0 \]

故 \(\bm x \in \ker(A) \iff \bm x \in \ker(A ^ \mathrm TA)\)，这证明 \(\ker(A) = \ker(A ^ \mathrm TA)\)．

另外有一种重要的特殊情况需要说明．若 \(A\) 是一个方阵，则

\[P = A(A^\mathrm TA)^{-1} A^\mathrm T = AA^{-1}(A^\mathrm T)^{-1}A^\mathrm T = I \]

这里需要强调最开始就给 \(A\) 提出的条件：列满秩，即列向量线性无关．在方阵中对应的是方阵可逆．

可逆方阵的列空间上，投影矩阵是 \(I\)．一个向量在可逆方阵的列空间上投影，就是向量本身．为何如此？因为可逆方阵的列空间就是整个空间，向量在整个空间上的投影当然是自己了．

最小二乘法

诚然，对于 \(A \bm x = \bm b\)，可能 \(\bm x\) 并没有一个解．然而，如果 \(A\) 是一个列满秩矩阵（瘦高的，\(r = n\) 的），则存在唯一的 \(\bm {\hat x}\)，使得 \(\left | \bm b - A \bm x \right |\) 取到最小值．这就是最小二乘法．

这个问题拥有相当强的直观意义．一句比较直观简洁的话描述：当 \(A \bm x = \bm b\) 无解时，我们可以退而求其次地对方程左乘 \(A ^ \mathrm T\)，变为 \(A ^ \mathrm TA \bm{\hat x} = A ^ \mathrm T\bm b\)．\(A\) 的列满秩性将会提供 \(A ^ \mathrm TA\) 的可逆性，进而提供 \(\bm{\hat x}\) 的可解性与唯一性．这样解出的 \(\bm {\hat x}\) 可让偏差 \(\bm e = \bm b - A \bm {\hat x}\) 模长最小．

最小二乘法可以解决线性拟合问题和二次拟合问题．甚至多次也是可以的．

以线性拟合为例．假设现在我们有一些点 \((t_1, b_1), (t_2, b_2), \ldots, (t_m, b_m)\)，则令

\[A = \begin{bmatrix} 1 & t_1 \\ 1 & t_2 \\ \vdots & \vdots \\ 1 & t_m \end{bmatrix}, \bm x = \begin{bmatrix} C \\ D \end{bmatrix}, \bm b = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} \]

根据最小二乘法我们能得到最小的 \(\left| \bm b - A \bm x \right|\)，这样的 \(\hat {\bm x}\) 则对应了我们找到的最佳线性拟合线：\(y = C + Dt\)．

这里需要一个小补丁：所有的 \(t_i\) 不能都相等．否则 \((t_1, t_2, \ldots, t_m)\) 就与 \((1, 1, \ldots, 1)\) 线性有关了．另外，必须有 \(m \ge 3\)．\(m = 2\) 的时候 \(A \bm x = \bm b\) 必有解，此时任意 \(\bm x\) 在 \(\operatorname{Im}(A)\) 上的投影就是自己，所以投影操作并没有什么意义．

有一个常见小操作：给所有的 \(t_i\) 减去 \(t_i\) 的平均值．这样操作后的结果是 \(\sum t_i = 0\)．好处是什么呢？

答案是操作后的 \(\sum t_i = 0\) 意味着刻画出的矩阵 \(A\) 满足第一列与第二列正交．进一步地，\(A\) 的列互相正交．

若 \(A\) 的列互相正交，则 \(A ^ \mathrm TA\) 是对角阵．
证明：考虑 \(A ^ \mathrm TA(i, j)\) 的意义，立得 \(i \ne j\) 时此式为 \(0\)．

我们知道对角阵解起来要方便地多，因此上面这个操作是非常具有价值的．这对应下一节的正交基与 Gram-Schmidt 正交化．

二次拟合的流程：

\[A = \begin{bmatrix} 1 & t_1 & {t_1}^2 \\ 1 & t_2 & {t_2}^2\\ \vdots & \vdots \\ 1 & t_m & {t_m}^2 \end{bmatrix}, \bm x = \begin{bmatrix} C \\ D \\ E \end{bmatrix}, \bm b = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} \]

此时需要的是 \(m \ge 4\)，以及所有的 \(|t|\) 不能都相等．

下面思考一个比较有趣的问题．假设所有的 \((t_i, b_i)\) 沿 \(y\) 轴对称，可以预测到 \(D = 0\)，即拟合出的二次曲线因为对称性，一次项应当为 \(0\)．上面的线性代数流程是如何体现这一点的？

答案是：\(A\) 的第二列与其他两列正交了．来看例子：

\[\begin{bmatrix} 1 & -2 & 4 \\ 1 & -1 & 1 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ 1 & 2 & 4 \end{bmatrix} \]

这里为了方便对称性的观察，按照 \(x\) 从小到大的顺序排列了．事实上这个顺序不影响，比如可以对换第一行第二行．

因为这种对称性，第二列与其他两列的点积是 \(0\)．思考 \(A ^ \mathrm TA\)（一个 \(3 \times 3\) 的方阵）的形态，可以得到它的 \((2, 1), (2, 3), (1, 2), (3, 2)\) 位置都是 \(0\)．

\[\begin{bmatrix} 5 & 0 & 10 \\ 0 & 10 & 0 \\ 10 & 0 & 34 \end{bmatrix} \]

再来思考 \(A ^ \mathrm T\bm b\) 的第二个数．它是 \(A\) 的第二列与 \(\bm b\) 的点积．根据对称性，仍然是 \(0\)．

从而考虑 \(A ^ \mathrm TA \bm {\hat x} = A ^ \mathrm T \bm b\) 时，由于 \(A ^ \mathrm TA\) 的第二行仅第二个数为 \(0\)，第二行与 \((C, D, E)\) 要点积得到 \(A ^ \mathrm T \bm b\) 的第二个数 \(0\)，必有 \(D = 0\)．

列正交矩阵与正交矩阵

向量组 \(\bm q_1, \bm q_2, \ldots, \bm q_n\) 是标准正交的，当且仅当

\[\bm q_i ^ \mathrm T \bm q_j = \begin{cases}0 & i \ne j \\ 1 & i = j\end{cases} \]

即，

• 每对向量正交．
• 每个向量均为单位向量．

根据这个定义，该向量组按列构成的矩阵 \(Q\) 满足

\[Q ^ \mathrm TQ = I \]

我们称这样的 \(Q\) 为列正交矩阵．这里 \(Q\) 不一定是方阵．若 \(Q\) 是方阵，则 \(Q^\mathrm T\) 将同时是 \(Q^{-1}\)，对于这种方阵的情形称 \(Q\) 是正交矩阵．正交矩阵必为方阵，这是定义规定的结果．

对于正交矩阵 \(Q\)，有

\[Q^\mathrm T Q = QQ^\mathrm T = I \]

换言之 \(Q^\mathrm T\) 一定也是正交矩阵，这是由方阵的逆是双侧逆得到的．

逆是转置的矩阵是正交矩阵．逆是自己的矩阵是对合矩阵．

验证一个矩阵 \(Q\) 是否是正交矩阵，最方便的方式就是验证 \(Q\) 是否是方阵，然后是 \(Q^\mathrm T Q= I\) 是否正确，即是否满足 \(Q\) 的列向量互相点积为 \(0\)，自己点积自己为 \(1\)．

注意列正交矩阵不一定有 \(QQ^\mathrm T = I\)．注意正交矩阵和列正交矩阵，虽然名字里只有正交，但都暗含了列向量均是标准的（模长为 \(1\)）．

另外，正交矩阵 \(Q\) 一定有 \(\det Q = \pm 1\)．这是因为 \(\det(I) = \det(QQ^\mathrm T) = \det(Q)\det(Q^\mathrm T) = \det(Q)^2\)．

三种正交变换

常见的正交矩阵有三种：旋转矩阵，置换矩阵，和反射矩阵．

\(n = 2\) 的旋转矩阵形如

\[\begin{bmatrix} \cos\theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \]

容易验证 \(QQ^\mathrm T = I\)．

\(Q\) 为旋转矩阵等价于 \(\det Q = 1\)．证明从略．

置换矩阵 是单位矩阵 \(I\) 经过任意次对换行后的结果．\(QQ^\mathrm T = I\) 容易验证．

反射矩阵．对于任意单位向量 \(\bm u\)，反射矩阵

\[Q = I - 2 \bm u \bm u^\mathrm T \]

值得注意的是，这样的 \(Q\) 同时具有对称性，即 \(Q^\mathrm T = Q\)．故反射矩阵 满足 \(Q^2 = QQ^\mathrm T = I\)．

证明反射矩阵 \(Q\) 是正交的：\(QQ^\mathrm T = Q^2 = (I - 2 \bm u \bm u ^\mathrm T)^2 = I - 4 \bm u (\bm u^\mathrm T \bm u) \bm u^\mathrm T + 4 \bm u \bm u^\mathrm T = I\)．这里 \(\bm u^\mathrm T \bm u\) 即 \(\| \bm u \|^2 = 1\)．

反射矩阵的作用是将向量在关于 \(\bm u\) 垂直的子空间平面上做镜像．故 \(Q^2 = I\) 意义明显：镜像两次得到自己．

反射矩阵具有这个效果，本质上是 \(\bm u \bm u^\mathrm T\) 成功起到了在 \(\bm u\) 上投影的效果．这是投影的一维特例．之前讲解投影时正是用一维引入的，这里可以视作那里的向量标准的特殊情况；也可以视作一会讲解的标准正交性简化投影里，投影空间一维的特殊情况．

正交矩阵 \(Q\) 作用于向量，称作正交变换．正交变换是保长变换，同时还是保角变换（本质是保内积）．上面的三个例子的几何意义明显地吻合了这两点．下面证明．

\[(Q\bm x)^\mathrm T(Q \bm x) = \bm x^\mathrm T (Q^\mathrm TQ) \bm x = \bm x^\mathrm T \bm x \]

故有保长性：

\[\| Q \bm x\| = \| \bm x\| \]

保角性：

\[(Q \bm x) ^\mathrm T (Q \bm y) = \bm x^\mathrm T (Q^\mathrm T Q) \bm y = \bm x^\mathrm T \bm y \]

保角性事实上是在证明保长性的基础上，又证明了保点积不变，从而证明保角性．

标准正交性简化投影

下面考虑在列正交矩阵 \(Q\) 上的投影是否有简单的性质，也就是选取投影空间 \(\bm V\) 的基时，我们选取了一组标准正交基．

我们知道投影的关键是找到 \(\bm {\hat x}\)：

\[A ^ \mathrm TA \bm{\hat x} = A ^ \mathrm T\bm b \]

若上面的 \(A\) 是列正交矩阵 \(Q\)，则 \(Q^\mathrm T Q = I\)．因此有

\[\bm{\hat x} = Q ^ \mathrm T\bm b \]

此时投影矩阵是 \(QQ^\mathrm T\)，投影向量 \(\bm p = QQ^\mathrm T \bm b\)：

\[\bm p = (QQ^\mathrm T)\bm b = (\bm q_1 \bm q_1^\mathrm T + \bm q_2\bm q_2 ^ \mathrm T + \cdots + \bm q_n \bm q_n^\mathrm T) \bm b = \bm q_1(\bm q_1^\mathrm T \bm b) + \bm q_2(\bm q_2^\mathrm T \bm b) + \cdots + \bm q_n(\bm q_n^\mathrm T \bm b) \]

这表明求解一个向量在列正交矩阵 \(Q\) 上的投影，只需要将 \(\bm b\) 在 \(Q\) 的每个列向量分别作投影，然后简单相加即可．这是正交性带来的性质，如果是任意矩阵，我们不能单纯地将向量投影到每个向量，然后将分量直接相加．

若 \(Q\) 是正交矩阵，此时投影矩阵为方阵，故 \(\bm p = \bm b\)．

\[\bm b = \bm q_1(\bm q_1^\mathrm T \bm b) + \bm q_2(\bm q_2^\mathrm T \bm b) + \cdots + \bm q_n(\bm q_n^\mathrm T \bm b) \]

Gram-Schmidt 与 QR 分解

Gram-Schmidt 可以将线性空间的任一组基转化为一组标准正交基．

第一步：正交化．其对于一组基 \(\bm a_1, \bm a_2, \ldots, \bm a_n\)，每枚举到一个 \(\bm a_i\)，考虑将其减去其对先前所有向量的投影．于是，这个 \(\bm a_i\) 将与先前的向量正交．这是一个 \(\Theta(n^2)\) 的算法．

第二步：标准化．将得到的所有向量都除以各自的模长．

在做题时，为了方便计算，算完每一个向量之后可以将其扩倍去掉分母，最后再统一标准化（即除以模长）．

Gram-Schmidt 的一大特点是，计算出的一组正交基 \(\bm q_1, \bm q_2, \ldots, \bm q_n\)，\(\bm q_i\) 不会与 \(j > i\) 的 \(\bm a_j\) 有关．换言之，\(\bm q_1, \bm q_2, \ldots, \bm q_k\) 和 \(\bm a_1, \bm a_2, \ldots, \bm a_k\) 这两个向量组互相可表，或者说张成的 \(k\) 维子空间完全一致．

因此我们有 \(A = QR\)．\(A\) 是 \(\bm a_1, \bm a_2, \ldots, \bm a_n\) 构成的矩阵．\(Q\) 是 \(\bm q_1, \bm q_2, \ldots, \bm q_n\) 构成的矩阵．\(R\) 是一个上三角阵．这里利用的是将 \(Q\) 的列视作列向量，\(R\) 的列视作线性组合系数的视角，即左列右列视角（不熟练的重新去看矩阵乘法一节）．

注意这里的 \(A\) 和 \(Q\) 可以是瘦高的阵．一般为了让 Gram-Schmidt 合理进行，\(A\) 需要是列满秩的（列向量线性无关）．\(R\) 一定是一个上三角方阵．

QR 分解对于计算最小二乘的 \(\bm{\hat x}\) 有什么作用？令 \(A = QR\)，我们要解

\[A^\mathrm T A \bm{\hat x} = A^\mathrm T \bm b \]

而

\[A^\mathrm T A = (QR)^\mathrm T(QR) = R^\mathrm T Q^\mathrm T QR = R^\mathrm TR \]

故

\[R^\mathrm TR\bm{\hat x} = R^\mathrm TQ^\mathrm T \bm b \]

而 \(R\) 一定是可逆的（对角线必无 \(0\)，因为第 \(k\) 个 \(\bm q_k\) 不可能由 \(\bm a_1, \bm a_2, \ldots, \bm a_{k - 1}\) 线性表出）．故

\[\bm{\hat x} = R^{-1}Q^\mathrm T \bm b \]

行列式

行列式的性质

方阵的行列式是一个标量值，但就是这样一个值蕴含了这个方阵相当多的信息量．

一个方阵 \(A\) 的行列式 \(\det A\)，可以被定义为方阵的满足三条基本属性的值．三条基本属性如下：

• \(\det I = 1\)．
• 对换两行，\(\det \to -\det\)．
• 行列式对于单独的某一行是线性函数．使用该性质时，其它行必须保持不变．

可以证明，对于每个方阵，按照三条基本性质定义出的 \(\det\) 一定存在且唯一．

另外非常值得注意的是，前两条基本性质决定了所有置换矩阵\(P\) 的行列式．其只可能取 \(1\) 或 \(-1\) 两种值．

三条基本属性可以推出七条其它也很有用的性质．具体如下．

性质四：若方阵的两行完全相同，则 \(\det A = 0\)．

证明：对换完全相同的两行，得到 \(\det A = -\det A\)，故 \(\det A = 0\)．

性质五：行倍加变换不改变 \(\det A\)．

证明（以 \(2 \times 2\) 方阵为例）：

\[\begin{vmatrix} a & b \\ c - \ell a & d - \ell b \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} - \ell \begin{vmatrix} a & b \\ a & b \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} \]

现在考虑高斯消元 \(A \to U\) 的过程．由于 \(A \to U\) 只有行置换与行倍加变换两种操作，故有

\[\det A = \pm \det U \]

性质六：有零行的矩阵 \(\det A = 0\)．

只需将任意行加到零行，则会出现完全相同的两行，故 \(\det A = 0\) 得证．

性质七：三角形矩阵 \(\det A = a_{11}a_{22}\cdots a_{nn}\)．

这是因为我们可以通过高斯消元 \(U \to D\)，整个流程只用到行倍增变换，故 \(\det\) 不变．

对 \(D\) 的每一行使用线性性拆出，令 \(D \to I\)，则拆出的系数之积即 \(\det D\)，即对角线元素的乘积．

性质八：\(A\) 的可逆性等价于 \(\det A \ne 0\)．

• 若 \(A\) 不可逆，则 \(\det A = 0\)．这是因为不可逆矩阵经过高斯消元 \(A \to U\) 后 \(U\) 会存在零行，故 \(\det A = \pm \det U = 0\)．
• 若 \(A\) 可逆，则 \(A \to U\) 后 \(U\) 的对角线上不会有零元．故 \(\det A \ne 0\)．

性质九：\(\det (AB) = \det A \det B\)．

这里有一个十分巧妙的证明．假设现在存在一个矩阵 \(B\)，若 \(\det B \ne 0\)，我们定义 \(A\) 的一个量为 \(D(A) = \dfrac{\det(AB)}{\det B}\)．则这个量满足三条基本性质：

• \(D(I) = \dfrac{\det B}{\det B} = 1\)．
• \(A\) 对换两行，则 \(AB\) 也会对换两行，故 \(D(A)\) 改变正负性．
• \(A\) 任一单独行的线性变换，会同步体现在 \(AB\) 的那一行．因此，\(D(A)\) 在单独行上也会满足线性性（考虑 \(\det B\) 是不变的系数，不会对 \(\det(AB)\) 的线性性造成影响）．

故 \(D(A)\) 完全满足行列式的三个基本性质，\(D(A)\) 就是 \(\det A\)．

下面还有一个 \(\det B = 0\) 的 corner case．只需证明 \(\det B = 0 \implies \det (AB) = 0\)，即 \(B\) 不可逆则 \(AB\) 一定不可逆．这是在第二章探讨过的结论．

性质十：\(\det A^\mathrm T = \det A\)．

证明：首先判掉 \(\det A = 0\) 的 corner case.然后，考虑 A 的 LU 分解：

\[PA = LU \]

对两侧取转置：

\[A^\mathrm T P^\mathrm T = U^\mathrm T L^\mathrm T \]

由于：

• \(\det L = \det L^\mathrm T = 1\)，因为二者对角线均为 \(1\)．
• \(\det U = \det U^\mathrm T\)，因为二者拥有相同的对角线．
• \(\det P = \det P^\mathrm T\)，因为 \(PP^\mathrm T = I\)，故 \(\det P \det P^\mathrm T = 1\)，而 \(\det P\) 与 \(\det P^\mathrm T\) 只能取 \(\pm 1\)，故 \(\det P = \det P^\mathrm T\) 只能取 \(1\) 或 \(-1\)．

对比即得 \(\det A = \det A^\mathrm T\)．

这条性质的意义是，直接证明先前所有行变换改成列变换，行列式的性质依旧成立．因为操作列等于先置换，再操作行，再置换回去．

一道有趣的题目．已知 \(3 \times 3\) 的矩阵 \(A\) 有行列式 \(\det A\)．用这个数表示下面这些由 \(A\) 经过某些操作后形成的矩阵的行列式．

• \(M_1\)：对 \(a_{ij}\) 乘 \((-1)^{i+j}\)，构造正负交替的棋盘格交替结构．
• \(M_2 = \begin{bmatrix}\textbf{row 1} - \textbf{row 3} \\ \textbf{row 2} - \textbf{row 1} \\ \textbf{row 3} - \textbf{row 2}\end{bmatrix}\)．
• \(M_3 = \begin{bmatrix}\textbf{row 1} + \textbf{row 3} \\ \textbf{row 2} + \textbf{row 1} \\ \textbf{row 3} + \textbf{row 2}\end{bmatrix}\)．

解答：

\[M_1 = \begin{bmatrix} 1 & & \\ & -1 & \\ & & 1 \\ \end{bmatrix} A \begin{bmatrix} 1 & & \\ & -1 & \\ & & 1 \\ \end{bmatrix} \quad \det M_1 = (-1) \det A (-1) = \det A \]

\(M_2\) 的行向量相加得 \(0\)，故 \(M_2\) 不可逆，\(\det M_2 = 0\)．

\(M_3\) 对每一行线性变换展开，得到 \(2^3 = 8\) 个展开式．

\[\begin{vmatrix}\textbf{row 1} + \textbf{row 3} \\ \textbf{row 2} + \textbf{row 1} \\ \textbf{row 3} + \textbf{row 2}\end{vmatrix} = \begin{vmatrix}\textbf{row 1} \\ \textbf{row 2}\\ \textbf{row 3}\end{vmatrix} + \begin{vmatrix}\textbf{row 3} \\ \textbf{row 2}\\ \textbf{row 3}\end{vmatrix} + \begin{vmatrix}\textbf{row 1} \\ \textbf{row 1}\\ \textbf{row 3}\end{vmatrix} + \cdots + \begin{vmatrix}\textbf{row 3} \\ \textbf{row 1}\\ \textbf{row 2}\end{vmatrix} \]

除了首项与末项，其余的矩阵行列式均为 \(0\)．首项与末项均为 \(\det A\)．故 \(\det M_3 = 2 \det A\)．

行列式的求解

行列式的求解有三种大体方案：

• 正负主元之积．高斯消元．注意由于行置换的影响，需要考虑一个正负号．
• 完全展开公式．\(n!\) 项．
• 余子式展开．递归地计算 \(n\) 个大小为 \(n - 1\) 的行列式．

为了充分考察这三种公式的优雅性质，我们选取一个优雅的矩阵．它是一个三对角线矩阵（tridiagonal，所有不满足 \(|i - j| \le 1\) 的元素 \(a_{ij} = 0\)），并令其中主对角线全 \(2\)，上下对角线全 \(-1\)．取不同的 \(n\) 可以得到这样不同的矩阵 \(A_n\)，下面是 \(n = 4\) 的一个例子．

\[A_4 = \begin{bmatrix} 2 & -1 & & \\ -1 & 2 & -1 & \\ & -1 & 2 & -1 \\ & & -1 & 2 \end{bmatrix} \]

可以证明：

\[\det A_n = n + 1 \]

下面用不同的求解视角证明这一点．

正负主元之积视角．或者说，高斯消元视角．刻画动态高斯消元操作的静态方式是 LU 分解．我们写出 \(A_n\) 的 LU 分解．

\[A_n = \begin{bmatrix} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & -1 & 2 & \ddots &\\ & & \ddots & \ddots & -1 \\ & & & -1 & 2 \end{bmatrix} = \begin{bmatrix} 1 & & & & \\ -\frac 1 2 & 1 & & & \\ & -\frac 2 3 & 1 & &\\ & & \ddots & \ddots & \\ & & & -\frac{n-1}n & 1 \end{bmatrix} \begin{bmatrix} 2 & -1 & & & \\ & \frac 3 2 & -1 & & \\ & & \frac 4 3 & -1 &\\ & & & \ddots & \ddots \\ & & & & \frac{n + 1}n \end{bmatrix} \]

观察 \(U\) 的主元之积，很明显其为 \(n + 1\)．又由于这里没有 \(P\) 的影响，故主元之积就是 \(\det A_n\)．

这个例子同时很好地展现了主元与行列式的关系．对于不涉及行置换的，高斯消元成可逆矩阵的情形，高斯消元的行与列是同步向下和向右扫的（感性理解一下，见高斯消元高观点）．扫到左上角 \(k \times k\) 的矩阵后，我们就做好了 \(A_k = L_k U_k\) 的分解，并且下一步将要做 \(A_{k + 1} = L_{k + 1} U_{k + 1}\)．

设 \(A_n\) 第 \(k\) 行（也是第 \(k\) 列）的主元为 \(d_k\)，则 \(\det A_k = d_1d_2\cdots d_k\)．即左上角子矩阵的行列式，反应了主元的前缀积．这个行列式称作 \(A_n\) 的 \(k\) 阶顺序主子式．在前缀积考虑差分（只不过是除法），得

\[d_k = \dfrac{\det A_k}{\det A_{k - 1}} \]

这就是主元与矩阵行列式的关系．对于不涉及行置换的，矩阵可逆的简单情形，每个主元都是邻阶顺序主子式之比．

想必第二章埋下的伏笔现在可以得到很好的解释．高斯消元不涉及行置换，条件是 \(A\) 的任一左上子方阵可逆．换言之，\(\det A_k \ne 0\) 恒成立．从上面的流程，我们容易看出这个条件的必要性．

完全展开式视角．

首先应当说明一下完全展开式公式为什么与先前行列式的定义吻合．其实，完全展开式就是暴力使用行列式的线性展开性质得到的．由于行列式的线性展开性质只允许我们一次拆一行，最初是一个 \(n \times n\) 的矩阵，我们对每一行做一次拆分，每次拆分将一个矩阵拆分为 \(n\) 个矩阵．所以最后 \(n \times n\) 的矩阵的 \(\det\) 会变成 \(n^n\) 个 \(\det\) 之和．

这 \(n^n\) 个 \(\det\) 的形态是这样的：每一行只保留一个元素，剩余元素全部置零．由于每一行有 \(n\) 种选法，总共有 \(n^n\) 种选法，故是 \(n^n\) 个 \(\det\)．

而这其中只有 \(n!\) 个 \(\det\) 是有效的．因为如果两行选了同一列，因为这两行其他元都是零元，故这两行构成倍数关系，导致 \(\det = 0\)．故，我们选取的元素是具有排列性的．行标与列标，都必须构成排列．

考虑 \(n!\) 个 \(\det\) 的每一项．我们可以将每个 \(\det\) 中，每一行的系数全部提出．这样剩下的 \(n!\) 个矩阵恰好是 \(n!\) 个置换矩阵．置换矩阵的行列式决定了 \(n!\) 项的符号，而这个行列式就是选取的行标列标逆序对的总数．

\(n = 3\) 的完全展开式是 \(6\) 项，有一个简单的记法，右下划线为正，左下划线为负．值得注意的是，\(n = 2\) 也符合这个结构，但 \(n \ge 4\) 时便不再符合，因为此时我们选择的元素并不一定构成一条斜线．

完全展开式适用于矩阵本身包含了大量 \(0\)的情形．如利用完全展开式，我们能够很轻松地看出三角矩阵的行列式为何是对角线的积．另外还可以考虑一种矩阵 \(Z\)：除了某一列外，剩下的列均为结构 \(I\)．

\[\det Z = \begin{vmatrix} 1 & 0 & a & 0 \\ 0 & 1 & b & 0 \\ 0 & 0 & c & 0 \\ 0 & 0 & d & 1 \end{vmatrix} = c \]

此类行列式将在克拉姆法则中大放异彩，拭目以待．

余子式展开．全展开将整个矩阵的行列式展开为 \(n!\) 项的和，而余子式展开让我们将整个矩阵的行列式展开为 \(n\) 项更小尺寸的 \(n-1\) 阶行列式之和．有点像递归．这是我们只使用了一次行列式的单行线性性的结果．

只使用一次行列式的单行线性性，假设我们用的是第 \(i\) 行，我们将矩阵拆成 \(n\) 个 \(\det\)，第 \(j\) 个 \(\det\) 满足第 \(i\) 行的第 \(j\) 列元素保留，其它均为 \(0\)．对该 \(\det\) 考虑完全展开，可以发现 \(a_{ij}\) 作为整行的唯一非零元必选．因此除了这一项，该 \(\det\) 剩下的展开项不会再考虑第 \(i\) 行和第 \(j\) 列（因为已被占用）——这就是余子式的结构．但严格来说，这两行去掉虽然不会影响具体的展开项，但可能会对负号有影响，考虑这个影响 \((-1)^{i+j}\) 后，就是代数余子式的结构．

形式化地，记矩阵 \(A\) 删掉第 \(i\) 行与第 \(j\) 列后，剩余元素构成大小为 \(n - 1\) 的矩阵 \(M_{ij}\)，则 \(\det M_{ij}\) 是 \(A_{ij}\) 的余子式，\(C_{ij} = (-1)^{i + j} \det M_{ij}\) 是 \(A_{ij}\) 的代数余子式．余子式展开：

\(\det A = a_{i1}C_{i1} + a_{i2}C_{i2} + \cdots + a_{in}C_{in}\)．

余子式展开适用于矩阵的某一行或者某一列包含了大量 \(0\)的情形．注意，按列展开也是可以的．回到最开始的例子：

\[\begin{vmatrix} 2 & -1 & & \\ -1 & 2 & -1 & \\ & -1 & 2 & -1 \\ & & -1 & 2 \end{vmatrix} = 2 \begin{vmatrix} 2 & -1 & \\ -1 & 2 & -1 \\ & -1 & 2 \end{vmatrix} - (-1) \begin{vmatrix} -1 & -1 & \\ & 2 & -1 \\ & -1 & 2 \end{vmatrix} = 2 \begin{vmatrix} 2 & -1 & \\ -1 & 2 & -1 \\ & -1 & 2 \end{vmatrix} - \begin{vmatrix} 2 & -1 \\ -1 & 2 \end{vmatrix} \]

即令 \(D_n = \det A_n\)，有

\[D_4 = 2D_3 - D_2 \]

类似地，

\[D_n = 2D_{n - 1} - D_{n - 2} \]

我们直接得到了 \(D\) 的一个二阶递推公式．只需计算初项 \(D_1 = 2\)，\(D_2 = 3\)，立得 \(D_n = n + 1\)．

这个做法比较强的一点是我们可以对 \(A_n\) 稍作一个修改，同样很快地计算出它的行列式：令 \(B_n\) 是 \(A_n\) 的 \((1, 1)\) 元素替换为 \(1\) 的结果．则 \(\det B_n\) 为？

此时 \(\det B_n = D_{n - 1} - D_{n - 2} = n - (n - 1) = 1\)．

下面来看另一个例子．海森堡矩阵是在三角阵的基础上再多一条对角线的矩阵．如下海森堡矩阵是下三角阵的基础上多一条上对角线．下面是一个海森堡矩阵：

\[H_n = \begin{bmatrix} 2 & 1 & & & \\ 1 & 2 & 1 & & \\ 1 & 1 & 2 & \ddots &\\ 1 & 1 & \ddots & \ddots & 1 \\ 1 & 1 & \cdots & 1 & 2 \end{bmatrix} \]

\(\det H_n\) 构成了斐波那契数列．为什么？

\[\begin{aligned} \det H_n &= \begin{vmatrix} 2 & 1 & & & \\ 1 & 2 & 1 & & \\ 1 & 1 & 2 & \ddots &\\ 1 & 1 & \ddots & \ddots & 1 \\ 1 & 1 & \cdots & 1 & 2 \end{vmatrix} \\ &= 2 \begin{vmatrix} 2 & 1 & & \\ 1 & 2 & \ddots &\\ 1 & \ddots & \ddots & 1 \\ 1 & \cdots & 1 & 2 \end{vmatrix} - \begin{vmatrix} 1 & 1 & & \\ 1 & 2 & \ddots &\\ 1 & \ddots & \ddots & 1 \\ 1 & \cdots & 1 & 2 \end{vmatrix} \\ &= 2 \det H_{n-1} - \begin{vmatrix} 2 & 1 & & \\ 1 & 2 & \ddots &\\ 1 & \ddots & \ddots & 1 \\ 1 & \cdots & 1 & 2 \end{vmatrix} + \begin{vmatrix} 1 & & & \\ 1 & 2 & \ddots &\\ 1 & \ddots & \ddots & 1 \\ 1 & \cdots & 1 & 2 \end{vmatrix} \\ &= 2\det H_{n - 1} - \det H_{n - 1} + \det H_{n - 2} \\ &= \det H_{n - 1} + \det H_{n - 2} \end{aligned} \]

故 \(\det H_n = (2, 3, 5, 8, \cdots)\)．

Cramer 法则解方程

第二章我们详尽地讨论了如何通过 Gauss-Jordan 算法求解 \(A \bm x = \bm b\)．这是相对工科的，算法的思路．这一节我们将探讨如何代数化这个流程．

Cramer 法则．考虑对 \(I\) 的第一列替换为 \(\bm x\)．

\[\begin{bmatrix} x_1 & 0 & 0 \\ x_2 & 1 & 0 \\ x_3 & 0 & 1 \end{bmatrix} \]

左乘 \(A\)，得到：

\[A \begin{bmatrix} x_1 & 0 & 0 \\ x_2 & 1 & 0 \\ x_3 & 0 & 1 \end{bmatrix} = \begin{bmatrix} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \end{bmatrix} = B_1 \]

对两边取行列式，得

\[(\det A) x_1 = \det B_1 \]

即

\[x_1 = \dfrac{\det B_1}{\det A} \]

求解 \(x_i\) 时，我们可以将 \(A\) 的第 \(i\) 列替换为 \(\bm b\)，得到方阵 \(B_i\)，并将新方阵和原方阵的行列式作比．

\[x_i = \dfrac{\det B_i}{\det A} \]

这就是Cramer 法则．

Cramer 法则求矩阵的逆（伴随矩阵）

下面研究矩阵的逆．对于

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \end{bmatrix} = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \]

对逆矩阵中的元素 \(x_1\)，\(x_2\)，\(y_1\)，\(y_2\) 考虑 Cramer 法则，会发现四个元素涉及到的行列式，正好是代数余子式的结构．如 \(x_1\) 涉及到的行列式是

\[\begin{vmatrix} 1 & b \\ 0 & d \end{vmatrix} = d \]

\(x_2\) 涉及到的行列式是

\[\begin{vmatrix} a & 1 \\ c & 0 \end{vmatrix} = -c \]

因为 Cramer 法则是将原矩阵 \(A\) 的一列替换成 \(I\) 的结构，即一行为 \(1\) 其它为 \(0\)，按这一列展开立即得到余子式的结构．换言之，对于求逆的过程，Cramer 法则的分母是原矩阵的 \(\det\)，而分子就是这个矩阵的某个代数余子式．

更具体而言，将代数余子式 \(C_{ij}\) 构成矩阵 \(C\)，我们有

\[A^{-1} = \dfrac{C^\mathrm T}{\det A} \]

\(C^\mathrm T\)，即代数余子式构成的矩阵的转置，称作伴随矩阵．可逆矩阵与伴随矩阵之间相差 \(\det A\) 的系数．

这也就是说，\(A^{-1}\) 的每一个元素可以视作一个 \(n-1\) 阶的行列式除以一个 \(n\) 阶的行列式．

下面是关于上面逆矩阵与伴随矩阵之间关系的一个直接证明．对这个式子变形得到

\[AC^\mathrm T = (\det A) I \]

推荐记忆这个形式，比较规整．

以 \(n = 3\) 的情形为例：

\[\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} = \begin{bmatrix} \det A & 0 & 0 \\ 0 & \det A & 0 \\ 0 & 0 & \det A \end{bmatrix} \]

用左行右列视角观察矩阵乘法，可以发现结果矩阵中的 \(\det A\) 的来源正是余子式展开的规则．那么 \(0\) 意味着什么呢？意味着类似余子式展开的结构，但是矩阵的一行在与代数余子阵的另一行在相乘，则最终结果为 \(0\)．这是因为矩阵的一行与代数余子阵的另一行相乘，本质上是在对另一个矩阵 \(A^\ast\) 做余子式展开，其中 \(A^\ast\) 中有相同的两行，故 \(\det A^\ast = 0\)．

这个结构是一类套路题，比如对

\[A = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 2 & 4 \\ 3 & 1 & 2 & 4 \\ 2 & 4 & 3 & 1 \\ \end{bmatrix} \]

求

\[C_{31} + C_{32} + C_{33} + C_{34} \]

实际是在求解

\[\begin{vmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 2 & 4 \\ 1 & 1 & 1 & 1 \\ 2 & 4 & 3 & 1 \\ \end{vmatrix} \]

即类余子式展开的结构，但是系数跟原矩阵没对上，实际上求的是另一个矩阵的 \(\det\)．翻译成另一个矩阵即可．

伴随矩阵不仅对满秩方阵（即可逆阵）有用，在秩比大小恰好少 \(1\) 的矩阵也有用途．考虑

\[AC^\mathrm T = (\det A) I = O \]

这是什么意思？考虑左乘变换视角，\(A\) 可以将 \(C^\mathrm T\) 的任一列湮灭，即 \(C^\mathrm T\) 的任一列向量属于 \(\ker(A)\)．注意 \(\dim \ker(A) = 1\)，\(C^\mathrm T\) 的列向量全部平行．

如果秩比 \(n\) 少 \(2\) 以上，伴随矩阵就显得比较平凡，一定是全 \(0\) 阵，因为秩比 \(n\) 少 \(2\) 以上，意味着任何一个代数余子式（对应一个 \(n - 1\) 大小的行列式）都是 \(0\)．

行列式求面积

我们熟知三角形面积公式．将一个点平移到原点 \((0, 0)\)，剩余两点坐标为 \((x_1, y_1)\)，\((x_2, y_2)\)，则面积

\[A = \dfrac{1}{2}\begin{vmatrix} x_1 & y_1 \\ x_2 & y_2 \end{vmatrix} \]

严格而论面积是非负的，上面的面积可以视作一种有向的面积，即交换两个向量会导致面积取相反值．非负面积再取个绝对值即可．

其背后的原理是，对应的平行四边形面积正好为

\[S = \begin{vmatrix} x_1 & y_1 \\ x_2 & y_2 \end{vmatrix} \]

即平面上两个向量围成的平行四边形的面积，是两个向量构成的行列式．一种证明方案是证明平行四边形的面积满足与行列式完全相同的三条基本定义，故面积就是行列式．

具体而言，设对应的矩阵为 \(A\)：

• 当 \(A = I\) 时，\(\det I = 1\)，而对应的平行四边形恰为单位正方形，面积也为 \(1\)．
• 交换两个向量，面积取相反值．
• 线性性，看下面的图片．

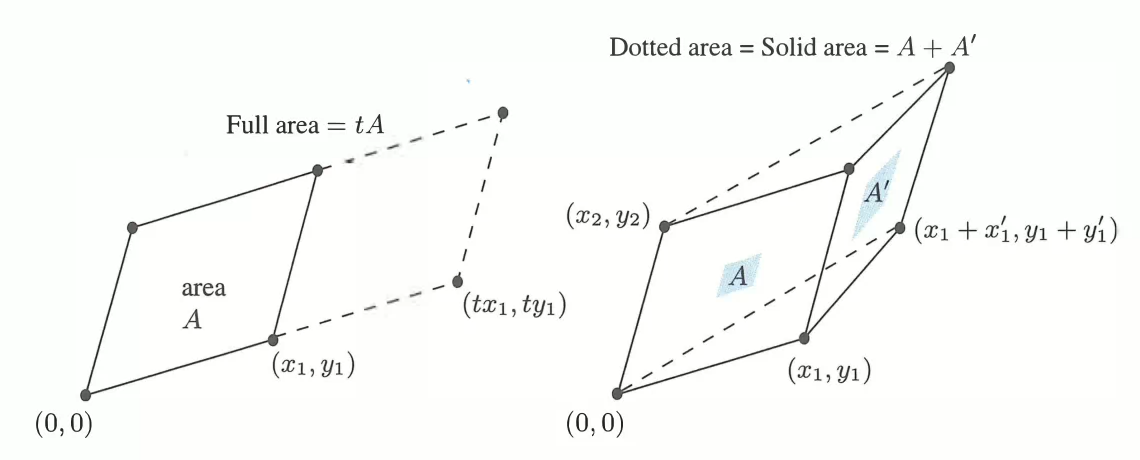
注意一种特殊情况：\(a \times b\) 的长方形对应的矩阵什么？恰好是对角阵：

\[\begin{vmatrix} a & 0 \\ 0 & b \end{vmatrix} = ab \]

上面的理论可以拓展到三维，此时计算的是平行六面体的体积．长方体对应了对角阵的行列式，恰为对角阵上元素（三条边长）的乘积．

Jacobi 行列式

Jacobi 行列式．假设我们现在想要计算一个二重积分：

\[\iint f(x, y) \mathrm d x \mathrm d y \]

这里的 \(\mathrm d x \mathrm d y\) 并不是简单的相乘关系，而是楔积．对这样的二重积分进行换元，如作极坐标系换元 \(x = r\cos \theta\)，\(y = r\sin \theta\)，对 \(\mathrm d x \mathrm d y\) 进行换元时，产生的系数是Jacobi 行列式．具体而言，

\[\mathrm d x \mathrm d y = \left | \dfrac{\partial(x, y)}{\partial(u, v)} \right | \mathrm d u \mathrm d v \]

其中

\[\dfrac{\partial(x, y)}{\partial(u, v)} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\[1em] \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix} \]

一元微积分中换元产生的系数是一个导数，即对 \(x = \varphi (u)\) 换元，有 \(\mathrm d x = \varphi'(u) \mathrm d u\)．上面的雅可比行列式是多元微积分中跟这个导数一样地位的东西．

叉积

叉积是三维向量特有的运算．叉积的结果仍然是一个三维向量．

\[\bm u \times \bm v = \begin{vmatrix} \bm i & \bm j & \bm k \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} \]

计算叉积时，对上面的行列式按第一行展开，得到答案向量中每一维的值．比较有趣的一点：答案向量第 \(i\) 维的值，与 \(u\)，\(v\) 第 \(i\) 维的值恰无关联．

叉积的一些性质：

• \(\bm v \times \bm u = -(\bm u \times \bm v)\)，因为 \(\bm v \times \bm u\) 相当于交换了行列式的两行．
• \(\bm u \times \bm v \perp \bm u\)．直接证明 \(\bm u \cdot (\bm u \times \bm v) = 0\) 即可，三重积形式稍后提到．
• \(\bm u \times \bm u = \bm 0\)，因为行列式中两行相同会得到 \(0\)．\(\bm u \parallel \bm v\) 时，也有 \(\bm u \times \bm v = 0\)，行列式两行平行也会得到 \(0\)．

\(\bm u \parallel \bm v \implies \bm u \times \bm v = \bm 0\)，\(\bm u \perp \bm v \implies \bm u \cdot \bm v = 0\)．前者涉及 \(\sin \theta\)，而后者涉及 \(\cos \theta\)：

• \(\| \bm u \times \bm v \| = \| \bm u \| \| \bm v \| | \sin \theta |\)．
• \(| \bm u \cdot \bm v | = \| \bm u \| \| \bm v \| | \cos \theta |\)．

\(\| \bm u \times \bm v \|\) 的值是 \(\bm u\) 与 \(\bm v\) 围成的平行四边形面积．

物理上，设 \(\bm r\) 是某个质点的位矢，\(\bm F\) 是施加在其的力，则 \(\bm r \times \bm F\)，即力矩，刻画了这个力对质点作用时，相对坐标原点的转动效果（坐标原点即位矢 \(\bm r\) 的起点．该矢量的终点是质点）．若 \(\bm r \times \bm F = \bm 0\)，即 \(\bm r \parallel \bm F\)，则无转动效果．否则，\(\bm r \times \bm F\) 的方向垂直于两个向量构成的平面，这个方向的刻画类似 \(\bm \omega\) 的方向对旋转方向的刻画（垂直于旋转面，且方向提供顺时针逆时针的信息）．

三重积．三重积形为 \((\bm u \times \bm v) \cdot \bm w\)，结果是一个标量，其意义为三个向量构成的平行四面体的体积．采用行列式的叉乘理解，容易看出三重积的行列式刻画：

\[(\bm u \times \bm v) \cdot \bm w = \begin{vmatrix} \bm i & \bm j & \bm k \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} \cdot \bm w = \begin{vmatrix} w_1 & w_2 & w_3 \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} \]

根据行列式的性质容易看出，对 \(u, v, w\) 进行 \(3! = 6\) 种排列，构成的 \(6\) 个三重积，分成两组．

• \((\bm u \times \bm v) \cdot \bm w = (\bm v \times \bm w) \cdot \bm u = (\bm w \times \bm u) \cdot \bm v\) 是一组．
• \((\bm v \times \bm u) \cdot \bm w = (\bm u \times \bm w) \cdot \bm v = (\bm w \times \bm w) \cdot \bm u\) 是一组．
• 两组之间互为相反数．

三重积为 \(0\)，当且仅当 \(\bm u, \bm v, \bm w\) 三向量共面．有三种角度理解这个：

• \(\bm u \times \bm v\) 垂直于这个平面，故 \(\bm w\) 与其点积为 \(0\)．
• 三重积对应的行列式，三个行向量 \(\bm u, \bm v, \bm w\) 线性相关，故行列式为 \(0\)．
• 共面的三个向量构成的平行四面体体积为 \(0\)．

特征值和特征向量

特征值和特征向量基本性质

特征值和特征向量都是方阵上的概念，故下面无特殊说明，大写字母，矩阵代指的都是方阵．

\[A \bm x = \lambda \bm x \]

当你对 \(A\) 的一个特征向量 \(\bm x\) 用 \(A\) 左乘作用时，向量的方向不发生改变．这里要求 \(\bm x \ne \bm 0\)，我们不认为零向量可以是特征向量．

变形得到

\[(A - \lambda I) \bm x = \bm 0 \]

由于 \(\bm x\) 是这个方程的一个非零解，故 \(\det (A - \lambda I) = 0\)．\(\det (A - \lambda I)\) 是 \(\lambda\) 的一个 \(n\) 次多项式，称作特征多项式．特征多项式的根即特征值．

由于是特征多项式是 \(n\) 次的，总共会有 \(n\) 个特征值．更准确地说，特征根的代数重数之和为 \(n\)．

对于每个特征根 \(\lambda\)，\(\dim \ker(A - \lambda I)\) 是该 \(\lambda\) 的几何重数，即这个特征根对应的特征空间的维度．特征空间是一个子空间，在这里的任何一个向量都满足 \(A \bm x = \lambda \bm x\)，所有的非零向量都是该 \(\lambda\) 对应的一个特征向量．

• 特征空间彼此直和．即，任一特征空间与（其余所有特征空间的和）的交仅零向量．
• 几何重数 \(\le\) 代数重数．
• 单位矩阵的 \(\lambda = 1\)，所有 \(\R^n\) 中的非零向量都是它的特征向量．数量矩阵的 \(\lambda\) 则是对角线上的数字．此时这个 \(\lambda\) 的代数重数和几何重数都是 \(n\)．
• 对角阵的特征值是对角线上的各元素．
• 三角阵的特征值也是对角线上的各元素．因为三角阵不可逆，也当且仅当对角线上有 \(0\)．
• 若 \(A\) 有特征值 \(\lambda\)，则任意常数 \(c\)，\(cA\) 有特征值 \(c\lambda\)．
• 矩阵可逆，等价于 \(\det A \ne 0\)，等价于矩阵没有特征值 \(0\)．
• 对于可逆矩阵 \(A\)，其一个特征值 \(\lambda\) 对应 \(A^{-1}\) 的一个特征值 \(\dfrac 1 \lambda\)，对应 \(C^\mathrm T\) 的一个特征值 \(\dfrac {|A|} \lambda\)，且三个特征值对应的特征空间完全相同．
• 对于矩阵 \(A\) 和其特征值 \(\lambda\)，\(A^k\) 有特征值 \(\lambda^k\)．\(\varphi(\lambda) = a_0 + a_1\lambda + a_2\lambda^2 + \cdots + a_m\lambda^m\) 是 \(\varphi(A) = a_0I + a_1A + a_2A^2 + \cdots + a_mA^k\) 的特征值．同一矩阵的多项式共享特征向量．
• Cayley-Hamilton 定理：任一方阵满足自己的特征方程．即任一方阵 \(A\) 的特征多项式为 \(\varphi(\lambda)\)，则 \(\varphi(A) = O\)．

我们可以将不是特征向量的向量分解到特征空间，来得到一些比较好的性质．比如

\[A = \begin{bmatrix} .8 & .3 \\ .2 & .7 \end{bmatrix} \]

可以用特征向量的观点分析出

\[A^{+\infty} \to \begin{bmatrix} .6 & .6 \\ .4 & .4 \end{bmatrix} \]

从而预测 \(A\) 的极高次幂的值．分析方法如下：

\(A\) 有两个特征值，\(\lambda = 1\) 和 \(\lambda = .5\)．其中，

• \(\lambda = 1\) 对应的特征空间是 \(\bm x_1 = (.6, .4)\) 张成的空间．
• \(\lambda = .5\) 对应的特征空间是 \(\bm x_2 = (1, -1)\) 张成的空间．

\(\bm x_1\) 和 \(\bm x_2\) 都是 \(A\) 的特征向量，将 \(A\) 作用于其将不改变方向．但由于特征值不同，特征向量被乘以它所对应的特征值，两个向量将展示不同的行为．

• \(\bm x_1\) 的特征值为 \(1\)，所以不断以 \(A\) 作用时，向量保持不变．
• \(\bm x_2\) 的特征值为 \(.5\)，所以不断以 \(A\) 作用时，向量衰减至零（每次向量长度变为原来的一半）．

故任意 \(\bm x\)，\(A^\infty \bm x\) 的结果正是 \(\bm x\) 在 \((.6, .4)\) 张成的子空间上的投影分量．因为这一分量保持，另一分量衰减至零．

将 \(A^\infty\) 视作 \(A^\infty A\)，所以问题就是对 \(A\) 的两个列向量分别考虑这个问题，故答案矩阵的每个列向量分别是 \(A\) 的列向量在 \((.6, .4)\) 张成的子空间上的投影分量．

这样的矩阵 \(A\) 称作马尔可夫矩阵（Markov Matrix）．这样的矩阵最大特征值为 \(1\)，该特征值张成的子空间是对应稳定态，而不在这个子空间的向量均会在高次幂中逐渐衰减．

投影矩阵是一种很特殊的马尔可夫矩阵．其只有 \(\lambda = 0\) 和 \(\lambda = 1\) 两个特征值．非稳定态向量的不稳定分量，只需一次 \(A\) 的作用便迅速衰减至零，展现出来就是投影的效果．马尔可夫矩阵则是在逐渐投影．

反射矩阵具有 \(\lambda = 1\) 和 \(\lambda = -1\) 两个特征值．\(\lambda = 1\) 对应的特征空间是镜面，而 \(\lambda = -1\) 对应的特征空间垂直于镜面．反射矩阵 \(R = I - 2P\)，其中 \(P = \bm u \bm u ^ \mathrm T\) 是一个一维投影矩阵．\(-2P\) 拥有特征值 \(0\)（镜面）和 \(-2\)（垂直镜面），而加 \(I\) 可以让矩阵的所有特征值平移 \(1\) 且保持对应特征空间不变，故特征值为 \(1\)（镜面）和 \(-1\)（垂直镜面）．

特征值性质两则

特征值有很特别的两个性质：

• 方阵的迹（trace）等于其特征值之和．
• 方阵的行列式等于其特征值之积．

对于 \(2 \times 2\) 的方阵，上面两个信息可以直接给出特征值的值．对于更大的方阵，特征值的求解仍需对特征多项式求根，但上面两个信息提供了一种检查的思路．

虚特征根

实矩阵可以有虚特征根．考虑旋转矩阵

\[Q = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \]

特征多项式给出 \(\lambda ^2 + 1 = 0\)，即 \(\lambda = \pm i\)．这很合理，没有非零实向量可以在旋转 \(90^\circ\) 下保持方向（但是虚向量可以）．

另外，所有的 \(|\lambda| = 1\) 是 \(Q\) 作为正交矩阵的体现（注意反射矩阵也符合这一点）；所有的 \(\lambda\) 均为纯虚数是 \(Q\) 作为反对称矩阵的体现．反过来，\(Q\) 作为实对称矩阵时特征根一定均为实数，非常重要的性质．

*Gershgorin 圆

对于任何一个 \(n \times n\) 的复矩阵 \(A\)，我们在复平面画 \(n\) 个圆．圆心为对角线上的 \(n\) 个元素（第 \(i\) 个圆圆心为 \(a_{ii}\)），第 \(i\) 个圆半径为 \(R_i = \sum_{j \ne i} |a_{ij}|\)，则这 \(n\) 个圆的并集一定覆盖所有特征值．称作 Gershgorin 圆．

原因是 \(A - \lambda I\) 不可逆，故 \(A - \lambda I\) 一定不是对角占优的．故一定存在一个 \(i\) 使得 \(a_{ii} - \lambda\) 不超过 \(R_i\)．

矩阵的对角化

在先前 \(A^\infty\) 的例子中，对角化的思想已经初见端倪．与其对于任意 \(\bm x\) 直接进行线性变换 \(A\)（\(A \bm x\)），我们选择将 \(\bm x\) 分解到特征空间上的若干特征向量，然后对这些特征向量分别数乘，再相加．

可以注意到这种简单性与对角阵做乘法非常相似．我们只是对若干个向量分别数乘相加，解开了不在对角线上的非零元素，造成的矩阵乘法里包含的向量间耦合．可以用对角化做到这一点．

对角化的流程如下．

假设 \(n \times n\) 的矩阵 \(A\) 有 \(n\) 个线性无关的特征向量，将它们构成矩阵 \(X\)．则 \(X^{-1}AX\) 即所求对角化矩阵 \(\Lambda\)．有 \(AX = X\Lambda\)．
对角化后，原矩阵的特征向量被保存到 \(X\)，特征值被保存到 \(\Lambda\)（对角线上的值）．

\[AX = A \begin{bmatrix} \bm x_1 & \cdots & \bm x_n \end{bmatrix} = \begin{bmatrix} \lambda_1 \bm x_1 & \cdots & \lambda_n \bm x_n \end{bmatrix} = \begin{bmatrix} \bm x_1 & \cdots & \bm x_n \end{bmatrix} \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{bmatrix} = X\Lambda \]

注意 \(A = X \Lambda X^{-1}\) 的高次幂有 \(A^k = X \Lambda^k X ^{-1}\)．这直接证明了 \(A^k\) 的特征值是 \(A\) 的特征值的 \(k\) 次方，且特征空间对应不变（\(X\) 不变）．注意这里 \(k = 0\) 和 \(k = -1\) 的时候也是成立的．

用这个观点可以轻松解释 \(A^\infty\) 问题：

\[A = \begin{bmatrix} .8 & .3 \\ .2 & .7 \end{bmatrix} = \begin{bmatrix} .6 & 1 \\ .4 & -1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & .5 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ .4 & -.6 \end{bmatrix} \]

故

\[A^k = \begin{bmatrix} .6 & 1 \\ .4 & -1 \end{bmatrix} \begin{bmatrix} 1^k & 0 \\ 0 & (.5)^k \end{bmatrix} \begin{bmatrix} 1 & 1 \\ .4 & -.6 \end{bmatrix} \]

\[A^\infty = \begin{bmatrix} .6 & 1 \\ .4 & -1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ .4 & -.6 \end{bmatrix} = \begin{bmatrix} .6 & .4 \\ .6 & .4 \end{bmatrix} \]

可对角化的条件是 \(X^{-1}\) 存在，上面保证其存在性的，是 \(A\) 有 \(n\) 个线性无关的特征向量．这即 \(A\) 可对角化的充要条件．

• \(A\) 有 \(n\) 个两两互异的特征值，则矩阵一定可对角化，因为其提供了 \(n\) 个彼此直和的一维线性特征空间．
• \(X\) 中的特征向量顺序与 \(\Lambda\) 中的特征值顺序是相同的，或者说按顺序对应的．从上面 \(AX = X\Lambda\) 的直观表述可以清晰地看到这一点．
• 可对角化性与可逆性无关联．可对角化性注重的是是否有足够的线性无关的特征向量，关注的是特征向量；而可逆性单纯注重特征值有没有零．

小 tips：可以用不可对角化的矩阵检验有关特征值和特征向量的表述正误．一般推翻这种表述的都是不可对角化的矩阵．

矩阵的相似

当我们将 \(A = X \Lambda X^{-1}\) 中的 \(\Lambda\) 固定，令 \(X\) 取任意可逆阵，得到的一系列 \(A\) 拥有相同的特征值（蕴含在 \(\Lambda\) 中）．这些 \(A\) 的关系是相似的．它们与 \(\Lambda\) 也是相似的，只需取 \(X = I\)．

矩阵的相似：对于任意方阵 \(A\) 和可逆阵 \(P\)，\(B = PAP^{-1}\)，则 \(A\) 和 \(B\) 相似，记作 \(A \sim B\)．

一个矩阵可对角化等价于其与一个对角阵相似．

相似矩阵一定是初等矩阵，因为 \(P\) 与 \(P^{-1}\) 都是可逆阵．故相似矩阵等秩．

相似矩阵拥有相同的特征值，所以行列式和迹也相同．这是因为假设 \(A\bm x = \lambda \bm x\)，则

\[B(P \bm x) = PAP^{-1}P \bm x = PA \bm x = \lambda P \bm x \]

即若 \(A\) 有特征值 \(\lambda\)，则 \(B\) 也有特征值 \(\lambda\)，且 \(B\) 在 \(\lambda\) 下的特征空间是 \(A\) 在 \(\lambda\) 下的特征空间进行了变换 \(P\) 的结果．相似是在变换特征空间．这个变换是可逆的．

当 \(A = I\) 时，其相似类只有自己 \(PIP^{-1} = I\)．与 \(I\) 相似的矩阵只有自己——它是唯一一个可对角化的所有 \(\lambda = 1\) 的矩阵．

如果不要求可对角化，相似类可以大一些．以 \(n = 2\) 为例，Jordan 对角型给出最简单的 \(A\)，此时对应的 \(B\) 是所有迹为 \(2\)，行列式为 \(1\) 的矩阵：

\[A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \quad B = \begin{bmatrix} 1 - rs & r^2\\ -s^2 & 1 + rs \end{bmatrix} \]

\(B\) 有 \(r\) 和 \(s\) 两个自由度．

再来一个 \(\lambda = 1\) 和 \(\lambda = 0\) 的例子．特征值不重复故一定可对角化．

\[\Lambda = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \quad A = \begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \text{ or } A = \begin{bmatrix} .5 & .5 \\ .5 & .5 \end{bmatrix} \text{ or any } A = \dfrac{\bm x \bm y^\mathrm T}{\bm x^\mathrm T \bm y} \]

此时相似类是所有满足 \(A^2 = A\) 的矩阵．这是广义投影矩阵（允许斜投影）．当 \(A\) 是对称矩阵时，即所有的正交投影矩阵．

线性递推问题

线性递推问题可以用特征值和特征向量很好地解决．最常见的一个例子是斐波那契数列．

考虑递推 \(\bm u_k = A^k \bm u_0\)．将 \(A\) 对角化为 \(X \Lambda X^{-1}\)，则 \(\bm u_k = X \Lambda^k X^{-1} \bm u_0\)．

现在用三步拆分这一项：

• 将 \(\bm u_0\) 写成特征向量 \(\bm x_i\) 的线性组合．\(\bm u_0 = c_1\bm x_1 + \cdots c_n \bm x_n\)，构造出系数向量 \(\bm c = X^{-1}\bm u_0\)．
• 对系数 \(c_i\) 乘以 \((\lambda_i)^k\)．此时得到 \(\Lambda^k X^{-1} \bm u_0\)．
• 然后再将这些系数对 \(\bm x_i\) 进行线性组合，即 \(X \Lambda^k X^{-1} \bm u_0\)．

\[\bm u_k = A^k \bm u_0 = X \Lambda^k X^{-1} \bm u_0 = X \Lambda^k \bm c = \begin{bmatrix}\bm x_1 & \cdots & \bm x_n\end{bmatrix}\begin{bmatrix} (\lambda_1)^k & & \\ & \ddots & \\ & & (\lambda_n)^k \end{bmatrix} \begin{bmatrix} c_1 \\ \vdots \\ c_n \end{bmatrix} \]

最终 \(\bm u_k = c_1(\lambda_1)^k\bm x_1 + \cdots + c_n(\lambda_n)^k\bm x_n\)，解决了线性递推问题．这里用到的基本想法是：分解到特征向量上考虑问题．

不可对角化性

如果一个特征值的代数重数是 \(1\)，则几何重数也必为 \(1\)．可以认为这样的特征值对可对角化性无影响．一个矩阵不可对角化，一定是因为其有一个特征值的代数重数 \(\ge 2\)，同时它的几何重数小于了代数重数，导致了线性无关特征向量数量的缺失．

举一个例子吧，矩阵

\[A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \]

拥有 \(\lambda = 0\)．其代数重数为 \(2\)，但几何重数是 \(1\)，这种维度的缺失导致了 \(A\) 的不可对角化．

可以用这个理论推一下：大小为 \(n\) 的全 \(1\) 矩阵特征值是什么？答案是代数重数，几何重数均为 \(n - 1\) 的 \(\lambda = 0\) 和重数为 \(1\) 的 \(\lambda = n\)．

分析一下为什么．首先全 \(1\) 矩阵的秩为 \(1\)，故 \(\dim \ker(A) = n - 1\)，即 \(\lambda = 0\) 的几何重数为 \(n - 1\)，其代数重数 \(\ge n\)．而 \(n\) 个特征值之和是矩阵的迹 \(n\)，故剩余的一个特征值为 \(1\)．

因此，任一矩阵的特征空间和为直和，而矩阵的可对角化性，刻画这个和是否充斥整个 \(\R^n\)．

Hadamard 阵．Hadamard 矩阵是一个 \(n \times n\) 的方阵 \(H\)，满足以下条件：

• \(H\) 中所有元素绝对值为 \(1\)．
• \(H^\mathrm T = H\)（\(H\) 是对称阵）．
• \(H^\mathrm TH = nI\)．即，\(H\) 的每个列向量是正交的，且模长为 \(\sqrt n\)（所有元素绝对值为 \(1\) 导致的模长必然结果）．

取 \(\dfrac{1}{\sqrt n} H\) 即可得到一个对称正交阵（再次注意正交阵这个名字暗含标准性）．它可以作为 \(A = (n + 1)I - J\) 的特征向量阵 \(X\)，其中 \(J\) 是全 \(1\) 阵，如 \(n = 4\) 时

\[\begin{bmatrix} 4 & -1 & -1 & -1 \\ -1 & 4 & -1 & -1 \\ -1 & -1 & 4 & -1 \\ -1 & -1 & -1 & 4 \end{bmatrix} \]

由于 \(-J\) 的特征值为 \(n - 1\) 个 \(0\) 和一个 \(-n\)，故 \(A\) 的特征值为 \(n - 1\) 个 \(n + 1\) 和一个 \(1\)．
\(\det A\) 的行列式为 \((n + 1)^{n - 1}\)，而其意义是 \(n + 1\) 个点的完全图的生成树个数．此为 Cayley 公式，\(n\) 个点完全图生成树个数为 \(n^{n - 2}\)．

特征值 \(1\) 对应一个特征向量是 \((1, 1, 1, 1)\)．由于 \(A\) 是实对称矩阵，其特征向量一定两两正交．故用带一个 \(\dfrac 1 {\sqrt n}\) 系数的 Hadamard 矩阵 \(H'\) 作为 \(X\) 是很合适的选择．

\[H' = \dfrac 1 2 H = \dfrac 1 2 \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} \]

\(H'\) 是对称正交阵，故 \(H' = (H')^\mathrm T = (H')^{-1}\)．于是，\(A^{-1} = H' \Lambda^{-1} H'\)．在这个例子中，\(A^{-1} = \dfrac 1 5 (I + J)\)．

微分方程（待补）

实对称矩阵——谱分解

任意矩阵特征空间的和是直和．即，任一特征空间，与（所有其它特征空间的和），交集平凡（仅零向量）．

对于实对称矩阵，有更强的结论：实对称矩阵的所有特征值一定均为实数，且特征空间两两正交，且 \(\dim\) 之和为 \(n\)．故实对称矩阵一定可对角化．

这个结论称作谱定理（Spectral Theorem）．先证特征值必为实数．假设 \(S \bm x = \lambda \bm x\)，两侧取共轭：

\[S \bm x = \lambda \bm x \implies S \bm{\bar x} = \bar \lambda \bm{\bar x}\quad \text{ transpose to } \quad \bm{\bar x}^\mathrm T S = \bm{\bar x}^\mathrm T \bar \lambda \]

对左右两端分别点乘一个 \(\bm{\bar x}\) 和 \(\bm x\)：

\[\bm{\bar x}^\mathrm T S \bm x = \bm{\bar x}^\mathrm T \lambda \bm x \]

\[\bm{\bar x}^\mathrm T S \bm x = \bm{\bar x}^\mathrm T \bar \lambda \bm x \]

注意到两个等式左侧相等，故右侧相等．\(\bm{\bar x}^\mathrm T \bm x > 0\)，故 \(\lambda = \bar \lambda\)．因此，特征值一定是实的．

再证来自不同特征空间的的特征向量一定正交．即 \(S \bm x = \lambda_1 \bm x\)，\(S \bm y = \lambda_2 \bm y\)，\(\lambda_1 \ne \lambda_2\)，证明 \(\bm x \perp \bm y\)．

\[\bm x^\mathrm T \lambda_1 \bm y = (\lambda_1 \bm x)^\mathrm T \bm y = (S\bm x)^\mathrm T\bm y = \bm x^\mathrm T S^\mathrm T \bm y = x^\mathrm TS \bm y = x^\mathrm T \lambda_2 y \]

由于 \(\lambda_1 \ne \lambda_2\)，故必有 \(\bm x^\mathrm T\bm y = 0\)，证毕．

其实目前距离证明实对称矩阵可对角化还差一步，即特征空间 \(\dim\) 和为 \(n\)，不过这里省略证明了（书中给的证明是 Schur 分解，不是很会）．

因为特征空间两两正交，故实对称矩阵来自不同特征空间的向量一定正交，即不同特征值对应的特征向量一定正交．

我们又知道，同一特征值对应的特征空间，假设重数（实对称矩阵任一特征值几何重数和代数重数相等，不必区分）为 \(d\)，则一定可以在这个特征空间找到一组大小为 \(d\) 的标准正交基（Gram-Schmidt）．

故，我们一定可以找到 \(n\) 个标准正交特征向量：

• 标准性手动约束保证．
• 来自同一特征空间的特征向量正交性由 Gram-Schmidt得到．
• 来自不同特征空间的特征向量正交性由实对称矩阵特征空间正交性自动保证．

对角化中这 \(n\) 个特征向量构成的 \(X\) 是正交矩阵，故用 \(Q\) 表示更合适．故

\[S = Q\Lambda Q^{-1} \]

进一步地，正交矩阵 \(Q^{-1} = Q^\mathrm T\)，故

\[S = Q\Lambda Q^\mathrm T \]

其还有另一形式：

\[S = \lambda_1 \bm q_1 \bm q_1^\mathrm T + \lambda_2 \bm q_2 \bm q_2^\mathrm T + \cdots + \lambda_n \bm q_n \bm q_n^\mathrm T \]

这个形式将 \(S\) 认为是若干投影矩阵的线性组合．\(\bm q_i \bm q_i^\mathrm T\) 是投影到向量 \(\bm q_i\) 的算子．线性组合的系数是特征值．所以这个操作也被称作谱分解．

上面是一种比较完全的谱分解．如果我们考虑将相同的 \(\lambda\) 合并，即认为总共 \(k\) 个本质不同特征值，则得到的会是 \(k\) 个投影矩阵的线性组合形式．此时投影算子的投影对象是这个特征值对应的整个特征空间．

事实上，任意对角化矩阵均能分解为投影算子的线性组合：这些投影算子的目标是特征空间，线性组合系数为对应的特征值．这些特征空间彼此直和（特征空间性质）且充满 \(\R^n\)（可对角化性保证），从而任一向量都可唯一分解到这些空间中，可对角化性提供投影分解的可行性，这也正是可对角化性的本质意义．

然而，若特征空间之间不正交，则我们采用的投影操作必须涉及斜投影．因为如果我们对一个向量在不正交的线性空间下强行做正交投影，则投影分量之和不再守恒于原向量，这就失去了投影的意义．然而，斜投影相对于标准正交投影（即本文一直讨论的投影所指），计算较为复杂且几何直观性弱．

所以，实对称矩阵和谱分解之所以在可对角化矩阵中，拥有极高的特殊性和简洁性，根本原因在于其特征空间两两正交．这种两两正交性使我们可以直接对任意向量做简单的正交投影，同时保证投影分量和的守恒于原向量．换言之，在一般的可对角化矩阵仅提供分解投影可行性的基础上，实对称矩阵进一步保证了分解可经完全的正交投影实现，从而保证了投影分解操作的几何直观性和计算简单性．故我们只为之冠名谱分解．

另外，考虑 \(n = 2\) 时，谱分解的形式为

\[S = Q\Lambda Q^\mathrm T = \begin{bmatrix} \bm q_1 & \bm q_2 \end{bmatrix} \begin{bmatrix} \lambda_1 & \\ & \lambda_2\\ \end{bmatrix} \begin{bmatrix} \bm q_1^\mathrm T \\ \bm q_2^\mathrm T \end{bmatrix} \]

正交矩阵行列式只有 \(\pm 1\) 两种情况．可以对 \(\bm q_2\) 的方向稍作调整，保证行列式为 \(1\)．此时 \(Q\) 一定是旋转矩阵，因为它一定可以写作这个形式：

\[\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \]

故 \(n = 2\) 的谱分解相当于在说，任何 \(2 \times 2\) 的对称阵变换，相当于先做了一次旋转操作，再进行一次伸缩操作，再进行一次旋转的逆操作．

对于不对称的矩阵，其特征值可能为复数．此时，特征值一定呈共轭对出现，因为 \(A\bm x = \lambda x \iff A \bm {\bar x} = \bar \lambda \bm {\bar x}\)．

矩阵的合同

若方阵 \(A\) 和 \(B\) 满足存在一可逆阵 \(P\) 使得 \(B = PAP^\mathrm T\)，称 \(A\) 与 \(B\) 合同，记作 \(A \simeq B\)．

合同矩阵一定是等价矩阵．原因也是 \(P\) 和 \(P^\mathrm T\) 可逆．

若 \(P\) 是正交矩阵 \(Q\)，则 \(Q^\mathrm T = Q^{-1}\)，此时即合同又相似，称这种关系为正交相似．

谱分解：实对称矩阵可以与一个对角阵正交相似．

Sylvester 惯性定理：合同变换保持方阵正特征值，负特征值和零特征值的数量不变．

实对称矩阵的惯性定理推论

先前得到的关系：特征值之积，主元之积，行列式三者相等（特别地，认为矩阵不可逆时主元之积是零）．

惯性定理推论：对于实对称矩阵 \(S = S^\mathrm T\) 的 \(n\) 个特征值和主元，正值、负值、零值数量对应相等．特别地，若正主元数量 / 正特征值数量为 \(n\)（即全正），称矩阵是正定的．

证明：不妨假设 \(S\) 可逆．考虑 \(S = LDL^\mathrm T\)，故 \(S\) 和 \(D\) 合同，使用Sylvester 惯性定理，故 \(S\) 的特征值与 \(D\) 的特征值正，负，零的数量均相同，而 \(D\) 的特征值即 \(D\) 的对角元素，刻画的正是 \(S\) 的主元．

下面给出一个不使用这个定理的证法（因为本文并没有证明惯性定理）．

\[\begin{bmatrix} 1 & 3\\ 3 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0\\ \bm 3 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & -8 \end{bmatrix} \begin{bmatrix} 1 & \bm 3\\ 0 & 1 \end{bmatrix} \]

考虑让 \(L\) 和 \(L^\mathrm T\) 渐变为 \(I\)．具体而言，对任意 \(i \ne j\)，考虑让 \(L_{ij}\) 和 \(L^\mathrm T_{ji}\) 同步渐变为 \(0\)．如上面是考虑将 \(3\) 渐变为 \(0\)．

此时 \(S\) 也会渐变，但是由于 \(D\) 不变，整个流程下 \(S'\) 的主元不发生变化．渐变后的结果 \(S' = IDI^{-1} = D\)，故渐变结果 \(S'\) 的特征值就是 \(D\) 的对角线，即 \(S\) 的主元．

同时 \(S'\) 的任何一个特征值不可能横跨了 \(0\)．因为只要有一个时刻 \(S'\) 有特征值 \(0\)，必有 \(S'\) 不可逆．但是 \(S' = L'DL'^\mathrm T\) 的主元一直是 \(D\) 的对角线元素，可逆性不可能消失．故整个流程下，特征值会变化，但一定不变号．变化的结果是主元，这就证明了惯性定理．

对合矩阵

下面来看一个综合性较强的简单例子．如果 \(A\) 的 \(\lambda = 1, -1\)，且特征向量 \(\bm x_1 = (\cos \theta, \sin \theta)\)，\(\bm x_2 = (-\sin \theta, \cos \theta)\)，可以推出 \(A\) 满足什么？

首先条件等价 \(\bm x_1 \perp \bm x_2\)．故 \(A\) 的两个特征空间正交．这意味着 \(A\) 是对称阵 \(A^\mathrm T = A\)．

观察 \(A^2\)．矩阵的幂不改变特征向量，只对特征值求幂．当两个不同的特征值求幂后相同，则发生特征空间的合并．这里 \(1^2 = (-1)^2\)，因此 \(A^2\) 的特征值是 \(1\)（代数重数 \(2\)），且其对应的特征空间是原先两个特征空间的和．特征空间的和是直和，故维度发生相加，合并为 \(2\)．故 \(A^2\) 的特征值 \(1\) 对应特征空间 \(\R^2\)，这意味着 \(A^2 = I\)．

或者使用 Cayley-Hamilton 定理，\(A\) 满足特征方程 \((\lambda - 1)(\lambda + 1) = 0\)，故 \((A - I)(A + I) = O\)，直接得到 \(A^2 = I\)．

\(A^2 = I\) 的矩阵称作对合矩阵．对合矩阵自动拥有一些性质：

• \(\det A = \pm 1\)．正交矩阵也满足这个性质．
• 自逆性．\(A = A^{-1}\)．
• 特征值 只能是 \(1\) 或 \(-1\)（反证立得）．
• 可对角化．证明从略．
• 考虑算子意义．做了两次等于没做？\(I\)，\(-I\)，反射矩阵，对换矩阵．

回到最开始那个例子．这个例子中 \(\det A = -1\)，因为特征值之积是 \(-1\)．惯性定理知，主元一定一正一负．

该例中的 \(A\) 是一个反射矩阵．对其谱分解，可知其作为一个算子时，被作用向量的 \(\bm{x_1}\) 方向的分量被保持，\(\bm{x_2}\) 方向的分量被反向．这明显是反射操作．

二阶差分矩阵的特征值

考虑下面两个二阶差分矩阵的特征值．

\[A_3 = \begin{bmatrix} 2 & -1 & \\ -1 & 2 & -1 \\ & -1 & 2 \end{bmatrix} \quad B_4 = \begin{bmatrix} 1 & -1 & & \\ -1 & 2 & -1 & \\ & -1 & 2 & -1 \\ & & -1 & 1 \end{bmatrix} \]

这两个矩阵作为算子作用在一个向量相当于对这个向量求二阶中心差分．我们可以类比二阶导，预测其特征向量的结构．注意二阶微分方程 \(\dfrac{\mathrm d^2 x}{\mathrm dt^2} = \lambda x\) 的解是三角函数，故特征向量 \(x = \sin kt\) 和 \(x = \cos kt\) 是 Fourier 级数的一组基．

*在补充微分方程这一节后完善这一节的剩余内容．

正定矩阵

所有的特征值全部为正数的实对称矩阵称作正定矩阵．其看起来具有比较强的特殊性，但是拥有非常广泛的应用．

正定矩阵的判定．事实上用定义判定正定矩阵，即找到所有的特征值并判断其均为正，称作特征值判定，一般是非常低效的方法．因为计算特征值要计算行列式，计算行列式并不是简单的操作．由于我们只需要知道所有特征向量的正负性而非具体值，这一判定拥有更高效的方案．下面研究更高效的方法，并学习正定矩阵的应用．

从 \(2 \times 2\) 的正定矩阵开始．\(S = \begin{bmatrix} a & b \\ b & c\end{bmatrix}\) 何时满足 \(\lambda_1 > 0\) 且 \(\lambda_2 > 0\)？

一种方法是顺序主子式判定，或称作Sylvester 准则：\(a > 0\) 且 \(\det S = ac - b^2 > 0\)．

证明：\(\lambda_1\lambda_2 = \det S = ac - b^2 > 0\)，故只需令迹 \(a + c > 0\)．显然 \(\det S > 0\) 得到 \(ac > 0\)，故只需令 \(a > 0\) 即可．这其实是 \(a\) 与 \(c\) 对称性的一种体现．

这里，\(a\) 应视作左上角 \(1 \times 1\) 的行列式，\(ac - b^2\) 应视作左上角 \(2 \times 2\) 的行列式．如果 \(n = 3\)，则需要加上 \(\det S > 0\) 这一 \(3 \times 3\) 的行列式判定．

另一种方法是主元判定．由于正定矩阵等价主元全正（惯性定理），故可以判定所有主元是否全为正．在 \(n = 2\) 时，这等价于 \(a > 0\) 且 \(\dfrac{ac - b^2}a > 0\)．

两个判定的等价性可以用主元和行列式的关系解释．这是在行列式一章讨论过的内容．顺序主子式是主元的前缀积，非常好地解释了上面两种判定的等价性．

二次型

二次型判定：\(S\) 是正定矩阵，当且仅当对于任意 \(\bm x \ne \bm 0\)，有 \(\bm x^\mathrm T S \bm x > 0\)．

二次型全正推特征值全正：对于任意特征向量有 \(\bm v^\mathrm T S \bm v > 0\)，故 \(\bm v^\mathrm T \lambda \bm v = \lambda \bm v^\mathrm T \bm v > 0\)，而 \(\bm v^\mathrm T \bm v = \| \bm v\| > 0\)，故 \(\lambda > 0\)．

特征值全正推二次型全正：对于任意 \(\bm x\)，有

\[\bm x^\mathrm T S \bm x = \bm x^\mathrm T (Q\Lambda Q^\mathrm T)\bm x = (Q^\mathrm T \bm x)^\mathrm T \Lambda (Q^\mathrm T \bm x) = \bm y^\mathrm T \Lambda \bm y = \lambda_1 {y_1}^2 + \lambda_2 {y_2}^2 + \cdots + \lambda_n {y_n}^2 > 0 \]

其中 \(\bm y = Q^\mathrm T \bm x\) 是 \(\bm x\) 经一个正交变换的结果，保长保内积．

由于 \(\bm x^\mathrm T S \bm x\) 的恒正性，这个数字（或者其一半，即 \(\frac 1 2 \bm x^\mathrm T S \bm x\)）经常被刻画为一个系统的能量．以 \(n = 2\) 为例：

\[\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} a & b \\ b & c \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = ax^2 + 2bxy + cy^2 > 0 \]

对角线上的元素提供平方项系数，而非对角线上的元素提供交叉项系数．

二次型同时给出正定性的可加性．若 \(S\) 和 \(T\) 是两个正定矩阵，则 \(S + T\) 同样正定．因为 \(\bm x^\mathrm T(S + T) \bm x = \bm x^\mathrm T S \bm x + \bm x^\mathrm T T \bm x > 0\)．主元和特征值在矩阵相加情形下没有很好的性质，但二次型作为能量的刻画保持了可加性．

先前我们提出任意 \(A^\mathrm TA\) 的两个性质：

• \(A^\mathrm TA\) 对角线非负（只要 \(A\) 没有全 \(0\) 列则恒正）．
• 当 \(A\) 列满秩 时，\(A^\mathrm TA\) 可逆．

现在我们给出另一性质：\(A\) 列满秩时，\(A^\mathrm TA\) 正定．因为

\[\bm x^\mathrm T(A^\mathrm TA)\bm x = (A \bm x)^\mathrm T(A \bm x) = \|A \bm x\|^2 \]

\(A\) 列满秩等价于 \(\dim \ker(A) = 0\)，故 \(\bm x \ne \bm 0\) 时 \(A \bm x \ne \bm 0\)，故上式恒正．

综上，我们给出了 \(S\) 正定的五种等价判定方式：

• 主元判定：\(S\) 的主元全正．
• 顺序主子式判定 / Sylvester 准则：\(S\) 的顺序主子式全正．
• 特征值判定：\(S\) 的特征值全正．
• 二次型判定：对于任意 \(\bm x \ne \bm 0\) 有 \(x^\mathrm T S \bm x > 0\)．
• \(S = A ^\mathrm TA\) 且 \(A\) 列满秩．此时 \(\|A \bm x\| = \bm x^\mathrm T S \bm x\) 是同一值．

正定矩阵 \(S = A^\mathrm T A\) 的分解方式不唯一．一种分解方式称作Cholesky 分解：

\[S = LDL^\mathrm T = (L\sqrt D)^{\mathrm T}(L \sqrt D) \]

取 \(A_2 = (L \sqrt D)^\mathrm T\) 即可，这是一个上三角矩阵（下三角的转置）．

另一种分解方式基于谱分解构造．令 \(S = Q\Lambda Q^\mathrm T\)，则可以取 \(A_3 = Q \sqrt \Lambda Q^{\mathrm T}\)．

这样构造出来的 \(A_3\) 满足 \(A_3\) 仍然是对称正定的，记作 \(S^{\frac 1 2}\)．它是满足 \(B^2 = S\) 的所有矩阵 \(B\) 中，必存在且仅存在一个的对称正定阵．

另外，对于任意分解 \(S = A^\mathrm T A\)，将 \(A\) 的某一行取反后也可以得到一个合法的分解．

半正定矩阵

半正定矩阵 \(\lambda\) 最小值为 \(0\)．故其不可逆．矩阵半正定等价于存在分解 \(S = A^\mathrm T A\)，其中 \(A\) 列不满秩．

还记得之前 \(\ker(A) = \ker(A^\mathrm T A) = \ker(S)\) 的结论吗？这个结论终于有了明确的意义：\(\bm x\) 在 \(S\) 下的能量 \(\bm x^\mathrm T S \bm x = 0\)，等价于 \(A \bm x = \bm 0\)，即 \(\bm x \in \ker(A)\)．

二次型几何直观

\(n = 2\) 时，考虑 \(\bm x^\mathrm T S \bm x = 1\) 的几何意义，即满足这个等式的所有 \(\bm x\) 在 \(\R^2\) 平面上构成什么．

设 \(\bm x = (x, y)\)，二次型等式即 \(ax^2 + 2bxy + cy^2 = 1\)．由于可能有 \(b \ne 0\) 的交叉项存在，椭圆可能是斜的．

现在考虑谱分解 \(S = Q \Lambda Q^\mathrm T\)，则

\[\bm x^\mathrm T S \bm x = \bm x^\mathrm T Q \Lambda Q^\mathrm T \bm x = (Q^\mathrm T \bm x)^\mathrm T \Lambda (Q^\mathrm T \bm x) \]

即 \(Q^\mathrm T \bm x\) 在二次型 \(\Lambda\) 意义下是一个正椭圆，因为 \(\Lambda\) 没有非对角线项，故椭圆没有交叉项．其含义为斜椭圆总能通过旋转变为正椭圆，\(Q^\mathrm T\) 为对应的旋转操作．

举一个例子：\(5x^2 + 8xy + 5y^2 = 1\)，等价于 \(S = \begin{bmatrix} 5 & 4 \\ 4 & 5\end{bmatrix}\) 对应的二次型．对角化：

\[\begin{bmatrix} 5 & 4 \\ 4 & 5\end{bmatrix} = \dfrac 1 {\sqrt 2} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 9 & 0 \\ 0 & 1 \end{bmatrix} \dfrac 1 {\sqrt 2} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \]

注意 \(\bm x = (x, y)\) 时，\(Q^\mathrm T \bm x = \left(\dfrac{x + y}{\sqrt 2}, \dfrac{x - y}{\sqrt 2}\right)\)，故谱分解的意义是：

\[5x^2 + 8xy + 5y^2 = 9\left( \dfrac{x + y}{\sqrt 2} \right)^2 + 1 \left( \dfrac{x - y}{\sqrt 2} \right)^2 \]

\(Q\) 蕴含了 \(S\) 的特征向量信息．两个特征向量

\[\bm q_1 = (1, 1) / \sqrt 2, \bm q_2 = (1, -1) / \sqrt 2 \]

分别指出了 \(S\) 对应二次型 \(= C\)（\(C\) 为任意正常数）时，椭圆 \(n = 2\) 个主轴的方向．故谱定理还有一个名字叫主轴定理，原因在于其指出了主轴方向．

\(\bm q_i\) 作为单位向量长度一定为 \(1\)，用来刻画椭圆主轴长度的是特征值．令 \(C = 1\)，则 \(n = 2\) 个主轴，每个半轴长等于对应的 \(1 / \sqrt \lambda\)．

总结．\(S\) 正定，则\(\bm x^\mathrm T S \bm x = 1\) 的图线是一椭圆：

\[\begin{bmatrix} x & y \end{bmatrix} Q \Lambda Q^\mathrm T \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} X & Y \end{bmatrix} \Lambda \begin{bmatrix} X \\ Y \end{bmatrix} = \lambda_1 X^2 + \lambda_2 Y^2 = 1 \]

椭圆的轴向是 \(S\) 的特征向量．椭圆的半轴长是特征值的 \(-\frac 1 2\) 次方．

\(S = I\) 时，对应的图线是单位圆 \(x^2 + y^2 = 1\)．若其中一个特征值反号，图线从椭圆变为双曲线，因为最后的平方加权和变成平方系数差，如 \(9X^2 - Y^2 = 1\)．若两个特征值均为负（负定），图像无点．

\(n > 2\) 的推广就是椭圆变成椭球．

Hessian 矩阵

正定矩阵的一个重要意义是探测多元函数的最值．

我们知道一元函数在 \(x_0\) 取最小值的一个充分条件是 \(f'(x) = 0\) 且 \(f''(x) > 0\)．（对于 \(f''(x) = 0\) 的情形，暂简化之）．

对于二元函数 \(F(x, y)\)，同样先检查 \(\frac{\partial F}{\partial x} = \frac{\partial F}{\partial y} = 0\)．然后，进一步检查 \(F\) 的二阶导．注意：我们需要对 \(\frac{\partial F}{\partial x}\) 和 \(\frac{\partial F}{\partial y}\) 分别对 \(x\) 和 \(y\) 再求偏导，所以一共会有 \(2 \times 2\) 项．同理，\(n\) 元函数的二阶偏导会有 \(n^2\) 项．将它们排列为矩阵：

\[S = \begin{bmatrix} \frac{\partial^2 F}{\partial x^2} & \frac{\partial^2 F}{\partial x \partial y} \\ \frac{\partial^2 F}{\partial y \partial x} & \frac{\partial^2 F}{\partial y^2} \end{bmatrix} \]

Clairaut 定理：\(\frac{\partial^2 F}{\partial x \partial y}\) 和 \(\frac{\partial^2 F}{\partial y \partial x}\) 若在 \((x, y)\) 有一方连续，则二者相等．这个定理直接给出 \(S\) 的对称性．这个对称阵称作Hessian 矩阵．

为了方便下面我们假设判定的是 \(F\) 在 \((0, 0)\) 的最值情况．在这里二阶泰勒展开：

\[G(x, y) = F(x, y) - F(0, 0) \approx ax^2 + 2bxy + cy^2 \]

则 Hessian 矩阵

\[\begin{bmatrix} 2a & 2b \\ 2b & 2c \end{bmatrix} \]

正是这个二阶泰勒展开的二次型．故

• \(F(0, 0)\) 是最小值，
• 当任意 \((\mathrm d x, \mathrm d y) \ne \bm 0\) 都有 \(G(\mathrm d x, \mathrm d y) > 0\)．
• *当且仅当任意 \((x, y) \ne \bm 0\) 都有 \(G(x, y) > 0\)．
• 当且仅当任意 \(\bm x \ne \bm 0\) 有 \(\bm x^\mathrm T S \bm x > 0\)．
• 当且仅当 \(S\) 正定．

故 Hessian 矩阵正定时，\(F(0, 0)\) 取最小值．同理总结：正定则最小，负定则最大，不定则鞍点，半正定 / 半负定则待定．

上面带 * 的当且仅当需要解释．事实上，\(\bm x^\mathrm T S \bm x\) 的正负性与 \(\| \bm x\|\) 无关．因为

\[(\lambda \bm x)^\mathrm T S (\lambda \bm x) = \lambda^2(\bm x^\mathrm T S \bm x) \]

故只要 \(\lambda \ne 0\) 则对正负性无影响．

Gilbert Strang 矩阵的特征值

Gilbert Strang 似乎很喜欢这个二阶差分矩阵呀，管它叫这个矩阵吧．

\[A_n = \begin{bmatrix} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & -1 & 2 & \ddots &\\ & & \ddots & \ddots & -1 \\ & & & -1 & 2 \end{bmatrix} \]

这个东西的特征值寒假详细研究下．

矩阵特征值特征向量属性对应表

线性变换

线性变换基础

变换是向量的函数，一般记作 \(T(\bm v)\)．

变换是线性的，当且仅当其满足以下两点：

• \(T(\bm v + \bm w) = T(\bm v) + T(\bm w)\)．
• \(T(c \bm v) = c T(\bm v)\)．

或：

• \(T(c\bm v + d \bm w) = cT(\bm v) + dT(\bm w)\)．

根据性质可以推出 \(T(\bm 0) = \bm 0\)．

• 平移变换是非线性的：\(T(\bm v) = \bm v + \bm u_0\)，它是非线性的．唯一的特例是 \(\bm u_0 = \bm 0\)，此时 \(T(\bm v) = \bm v\) 是一个恒等变换，它是非常特殊的一种线性变换．
• 仿射变换是非线性的：\(T(\bm v) = A \bm v + \bm u_0\)，是线性变换与平移变换的结合．
• 与常向量点积的变换是线性的：\(T(\bm v) = \bm v \cdot \bm u_0\)．设 \(\bm v\) 是 \(n\) 维向量，则 \(T\) 的定义域为 \(\R^n\)，值域为 \(\R^1\)．
• 若变换结果含有平方项、交叉项、模长，变换不线性（\(v_1^2\)，\(v_1v_2\)，\(\|\bm v\|\)）．如 \(T(\bm v) = \|\bm v\|\) 显然不线性．
• 旋转变换是线性的．如 \(T(\bm v)\) 将 \(\bm v\) 顺时针旋转 \(30^\circ\)．该 \(T\) 定义域和值域相同．在这个线性变换下，整个空间都在旋转．

线性变换有两个性质刻画线性性．下面假设所有向量的起点都是原点．

保共线性：若 \(\bm u\)，\(\bm v\)，\(\bm w\) 终点共线，则 \(T(\bm u)\)，\(T(\bm v)\)，\(T(\bm w)\) 终点也共线．

保比例性：若 \(\bm u\)，\(\bm v\)，\(\bm w\) 终点共线，且 \(\bm u\) 终点将线段 \(\bm v \bm w\) 按照一定的比例切分，则 \(T(\bm u)\)，\(T(\bm v)\)，\(T(\bm w)\) 终点仍共线（保线性性）的同时，\(T(\bm u)\) 会将 \(T(\bm v)T(\bm w)\) 按照相同的比例切分．

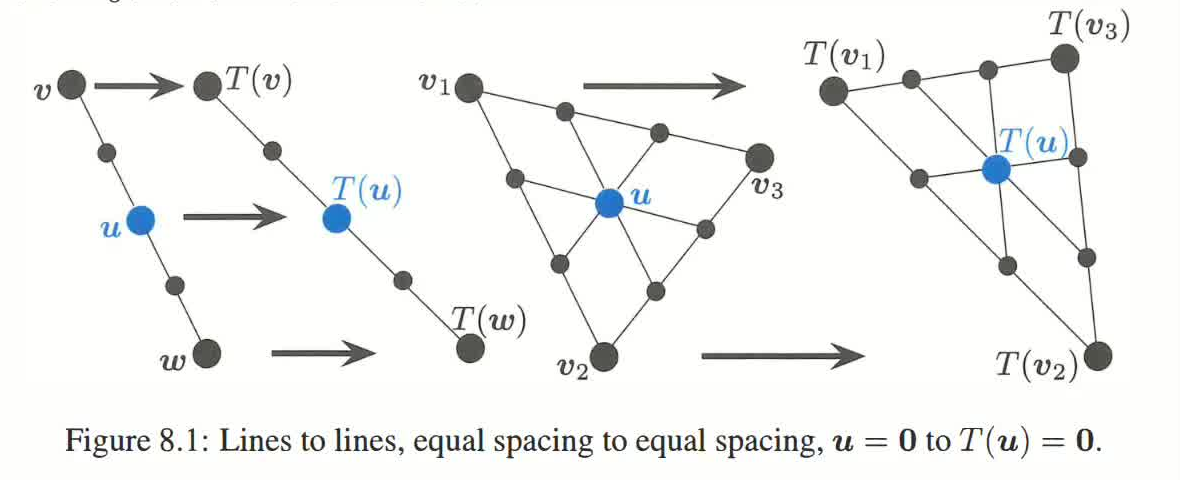
这种线性性可以推广到 \(n\) 向量：若

\[\bm u = c_1 \bm v_1 + c_2 \bm v_2 + \cdots + c_n \bm v_n \]

则

\[T(\bm u) = c_1 T(\bm v_1) + c_2 T(\bm v_2) + \cdots + c_n T(\bm v_n) \]

这引出线性变换最重要的事实：若 \(T\) 的定义域是 \(n\) 维线性空间 \(D\)，只需要知道 \(D\) 的 \(n\) 个基 \(\bm v_i\) 线性变换后 \(T(\bm v_i)\) 的结果，即可知任意 \(\bm u \in D\) 线性变换后 \(T(\bm u)\) 的结果．因为上面的线性性告诉我们：\(\bm u\) 是 \(\bm v_i\) 的某个线性组合，则 \(T(\bm u)\) 也是 \(T(\bm v_i)\) 系数完全相同的线性组合．

过渡矩阵