损失函数

个人学习所用，内容来源于网络，侵权删。

1. 定义

损失函数是用来评价网络模型的输出的预测值\(\widehat{Y}=f(X)\)与真实值\(Y\)之间的差异，我们使用\(L(Y, \widehat{Y})\)来表示损失函数（非负实值函数），我们的目的是让损失函数尽可能小。
假设网络模型中有\(N\)个样本，样本的输入和输出向量为\((X,Y)=(x_i, y_i), i\in[1,N]\)，则损失函数为每一个预测值与真实值的差之和。

\[L(Y, \widehat{Y})=\sum_{i=0}^Nl(y_i,\widehat{y_i})^2 \]

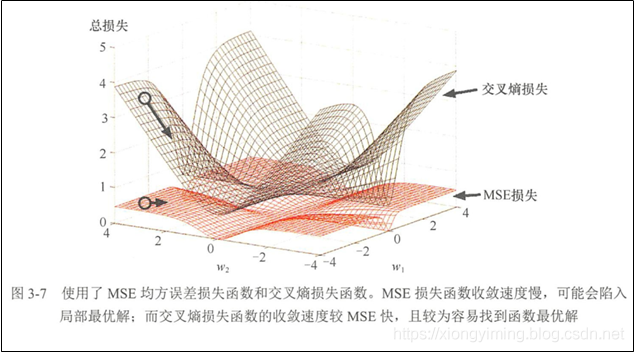
在BP神经网络中，一般推导中，使用均方误差作为损失函数，而在实际中，常用交叉熵作为损失函数。如上图所示，我们可以清晰地观察到不同的损失函数在梯度下降过程中的收敛速度和性能都是不同的。

• 均方误差作为损失函数收敛速度慢，可能会陷入局部最优解；
• 而交叉熵作为损失函数的收敛速度比均方误差快，且较为容易找到函数最优解.

2. 回归损失函数

(1)均方差损失函数(MSE)

\[L(Y, \widehat{Y})=\frac{1}{N}\sum_{i=0}^N(\widehat{y_i}-y_i)^2 \]

(2)平均绝对误差损失函数(MAE)

\[L(Y, \widehat{Y})=\frac{1}{N}\sum_{i=0}^N|\widehat{y_i}-y_i| \]

(3)均方误差对数损失函数(MSLE)

\[L(Y, \widehat{Y})=\frac{1}{N}\sum_{i=0}^N(\log\widehat{y_i}-\log y_i)^2 \]

(4)平均绝对百分比误差损失函数(MAPE)

\[L(Y, \widehat{Y})=\frac{1}{N}\sum_{i=0}^N\frac{100\cdot|\widehat{y_i}-y_i|}{y_i} \]

(5)小结

均方误差损失函数是使用最广泛的，并且在大部分情况下，均方误差有着不错的性能，因此被用作损失函数的基本衡量指标。MAE 则会比较有效地惩罚异常值，如果数据异常值较多，需要考虑使用平均绝对误差损失作为损失函数。一般情况下，为了不让数据出现太多异常值，可以对数据进行预处理操作。
均方误差对数损失与均方误差的计算过程类似，多了对每个输出数据进行对数计算，目的是缩小函数输出的范围值。平均绝对百分比误差损失则计算预测值与真实值的相对误差。均方误差对数损失与平均绝对百分 比误差损失实际上是用来处理大范围数据( [ − 10 5 , 10 5 ]的，但是在神经网络中，我们常把输入数据归一化到一个合理范围 ( [ − 1 , 1 ])，然后再使用均方误差或者平均绝对误差损失来计算损失。

3. 分类损失函数

(1). Logistic损失函数

\[L(Y, \widehat{Y})=\prod_{i=0}^N\widehat{y_i}^{y_i}\cdot(1-\widehat{y_i})^{1-y_i} \]

(2). 负对数似然损失函数

\[L(Y, \widehat{Y})=-\sum_{i=0}^Ny_i\cdot\log\widehat{y_i}+(1-y_i)\cdot\log(1-\widehat{y_i}) \]

(3). 交叉熵损失函数

\[L(Y,\widehat{Y})=\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{M}y_{i,j}\cdot\log\widehat{y}_{i,j} \]

(4). Hinge损失函数

\[L(Y,\widehat{Y})=\frac{1}{N}\sum_{i=1}^{N}max(0,1-\widehat{y}_i\cdot y_i) \]

(5). 指数损失函数

\[L(Y,\widehat{Y})=\sum_{i=1}^{N}e^{-\widehat y_i\cdot y_i} \]

4. 神经网络中常用的损失函数

(1)ReLu + MSE

均方误差损失函数无法处理梯度消失问题，而使用 Leak ReLU 激活函数能够减少计算时梯度消失的问题，因此在神经网络中如果需要使用均方误差损失函数，一般采用 Leak ReLU 等可以减少梯度消失的激活函数。另外，由于均方误差具有普遍性，一般作为衡量损失值的标准，因此使用均方误差作为损失函数表现既不会太好也不至于太差。

(2)Sigmoid + Logistc

Sigmoid 函数会引起梯度消失问题：根据链式求导法，Sigmoid 函数求导后由多个［0, 1］范围的数进行连乘，如其导数形式为 ，当其中一个数很小时，连成后会无限趋近于零直至最后消失。而类 Logistic 损失函数求导时，加上对数后连乘操作转化为求和操作，在一定程度上避免了梯度消失，所以我们经常可以看到Sigmoid激活函数＋交叉摘损失函数的组合。

(3)Softmax + Logistc

在数学上，Softmax 激活函数会返回输出类的互斥概率分布，也就是能把离散的输出转换为一个同分布互斥的概率，如(0.2, 0.8)。另外，Logisitc 损失函数是基于概率的最大似然估计函数而来的，因此输出概率化能够更加方便优化算法进行求导和计算，所以我们经常可以看到输出层使用Softmax激活函数＋交叉熵损失函数的组合。

参考来源：
深度学习-常用损失函数详细介绍

5. 激活函数、损失函数、优化函数的区别
(1) 激活函数：将神经网络上一层的输入，经过神经网络层的非线性变换转换后，通过激活函数，得到输出。常见的激活函数包括：sigmoid, tanh, relu等。
[深度学习]神经网络的激活函数

(2) 损失函数：
度量神经网络的输出的预测值，与实际值之间的差距的一种方式。常见的损失函数包括：最小二乘损失函数、交叉熵损失函数、回归中使用的smooth L1损失函数等。

(3) 优化函数：
也就是如何把损失值从神经网络的最外层传递到最前面。如最基础的梯度下降算法，随机梯度下降算法，批量梯度下降算法，带动量的梯度下降算法，Adagrad，Adadelta，Adam等。
[深度学习]梯度下降算法、优化方法（SGD,Adagrad,Adam...)

参考来源：
深度学习知识点全面总结