6.牛顿迭代法求方程根

 

 

问题分析：

首先，设fx=axˆ3+bxˆ2+cx+d，则可在坐标图上画出fx。此时fx与横坐标的交点即为方程的，现在来求这个解的值
当x0=1时，fx=ax0ˆ3+bx0ˆ2+cx0+d
在(x0,fx)上作fx的切线，切线的斜率f为fx求导，得f=3axˆ2+2bx+c，交横坐标于(x1,0)点
根据三角函数定理，有f=fx/(x0-x1)，转换得x1=x0-fx/f
可以看到，x1比x0离方程的解更接近
此时在(x1,fx1)上进行上述同样的操作。可以看到，切线与横坐标的交点离方程的解越来越近
如此循环，可以设置当(x1-x0)的绝对值小于1e-5即停止循环，最后的x1即为方程的近似解，可以通过放大或缩小1e-5的值来获得更为粗略或者精确的解

 

 

 

 

流程图：

 

 

 

 

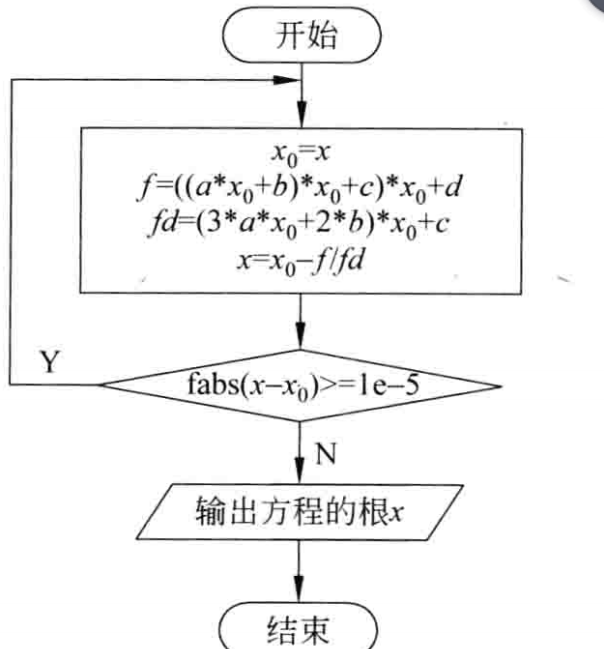
代码：

#include <stdio.h>
#include <math.h>
int main()
{
double newton_method(int a, int b, int c, int d);
int a,b,c,d;
double root;
printf("please enter a,b,c,d: ");
scanf("%d %d %d %d",&a,&b,&c,&d);
root=newton_method(a,b,c,d);
printf("The root is: %f\n",root);
return 0;
}

double newton_method(int a, int b, int c, int d)
{
double x1,x0,fx,f;
x1=1.0;
while(fabs(x1-x0)>=1e-5)
{
x0=x1;
fx=a*x0*x0*x0+b*x0*x0+c*x0+d;
f=3*a*x0*x0+2*b*x0+c;
x1=x0-fx/f;
}
return(x1);
}