2021-06-24

思维量大 + 代码短

拿到这种题，我们一定是要自己思考，而且是把所有可能正确的贪心做法都试一遍的。

level 1

我们只考虑使用时间最少的洗衣机和烘干机，可以分 $w[1]\ge d[1]$ 和 $w[1]\le d[1]$ 两种情况讨论，答案是 $max(w[1],d[1])\ast l+min(w[1],d[1])$ 。

期望得分 $10pts$。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll l, n, m;
ll w[100005], d[100005];
//level 1
int main() {
    //  freopen("data.in","r",stdin);
    scanf("%lld%lld%lld", &l, &n, &m);

    for (int i = 1; i <= n; i++) {
        scanf("%lld", &w[i]);
    }

    sort(w + 1, w + 1 + n);

    for (int i = 1; i <= m; i++) {
        scanf("%lld", &d[i]);
    }

    sort(d + 1, d + 1 + m);
    printf("%lld", max(w[1], d[1])*l + min(w[1], d[1]));
}

level 2

考虑让最后一个洗干净的衣服尽量早，可以用优先队列模拟这个过程，对于每一件衣服，找结束时刻最早的洗衣机进行操作。

同样考虑烘干操作，找到最晚烘干所需的时间。

不难发现，所求的答案一定是大于最优答案的。

期望得分 $10pts$。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll l, n, m;
ll w[100005], d[100005];
struct node {
    ll val;
    ll d;
    bool operator <(const node &a) const {
        return val + d > a.val + a.d;
    }
};
priority_queue<node> q, q2;
//level 2
int main() {
    //  freopen("data.in","r",stdin);
    scanf("%lld%lld%lld", &l, &n, &m);

    for (int i = 1; i <= n; i++) {
        scanf("%lld", &w[i]);
        q.push((node) {
            0, w[i]
        });
    }

    sort(w + 1, w + 1 + n);

    for (int i = 1; i <= m; i++) {
        scanf("%lld", &d[i]);
        q2.push((node) {
            0, d[i]
        });
    }

    sort(d + 1, d + 1 + m);

    for (int i = 1; i <= l; i++) {
        node x = q.top();
        q.pop();
        q.push((node) {
            x.val + x.d, x.d
        });
    }

    for (int i = 1; i <= l; i++) {
        node x = q2.top();
        q2.pop();
        q2.push((node) {
            x.val + x.d, x.d
        });
    }

    //b min{机器等待的时间 + 工作的时间}
    ll res = 0, res2 = 0;

    while (q.size()) {
        res = max(res, q.top().val);
        q.pop();
    }

    while (q2.size()) {
        res2 = max(res2, q2.top().val);
        q2.pop();
    }

    printf("%lld", res + res2);
}

level 3

结合 $level2$　的算法，我们可以对于每一件衣服分别考虑，求出所有衣服中完成清洗、烘干两次操作最晚的时间。

考虑第 $i$ 件衣服，首先等待前 $i-1$ 件洗完的时间是 $val$ + $d$ (自己洗完的时间)

注意到前 $i-1$ 件衣服一定先烘干，但是先洗完的衣服烘干会占用烘干机的位置，然后安排前 $i-1$ 件衣服在自己后面烘干 (平衡两次相加的总时间)

期望得分 $100pts$。

下面我们来证明一下这个算法为什么是对的。

我们来证明这个做法得到的答案 既不会比最优解优，也不会比最优解劣 。

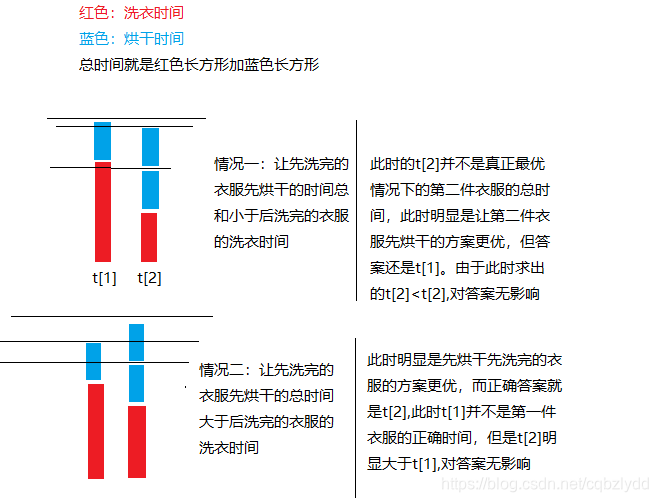
可以看到，我们所担心的 先洗净的衣服会增加答案的情况是不会出现的（因为最晚洗完的衣服已经分配了最优的烘干方案），因为如果让先洗完的衣服后烘干的时间更晚的话，我们后洗净的衣服必须等待先洗净的衣服烘干完，而它 等待到的时刻+烘干的时间 恰好就是答案。

证毕。

总结

这样抽象的算法自己还是比较难想到的。

我的思维水平也就在 $level2$ ，正解只能想一半。