【题解】「abc171F」Strivore
题意
求出在一个字符串 s s s 中插入 n n n 个小写字母,有多少不同的结果。 n ≤ 1 0 6 n\leq 10^6 n≤106 。
solution:
神仙计数题。本题可以等价转化为,有多少长度为 n + m n+m n+m 的字符串存在子序列串 s s s 。为了避免算重,我们规定如果有相同字符,则取序列中的最后一个 。
例如:字符串 abbcddc 的子序列 bc,从字符串的结尾往开头找,c 找到字符串末尾,b 找到字符串第三位。不难发现,对于一个给定的字符串所对应的唯一子序列是确定的。
那么我么就可以考虑枚举开头位置 1 ≤ i ≤ m + 1 1\leq i \leq m+1 1≤i≤m+1 , i i i 前面的每一个数都没有限制,总共 2 6 i − 1 26^{i-1} 26i−1 种可能。对于后面 n + m − i n+m-i n+m−i 个数,首先选出 m − 1 m-1 m−1 个数确定子序列在字符串中的位置;对于剩下 n − i + 1 n-i+1 n−i+1 个不在子序列中的数,为了满足定义,我们知道不能和它后继的子序列中的字符一样,所以总共 2 5 n − i + 1 25^{n-i+1} 25n−i+1 种可能。
如图,可以发现的确有 25 25 25 种可能。
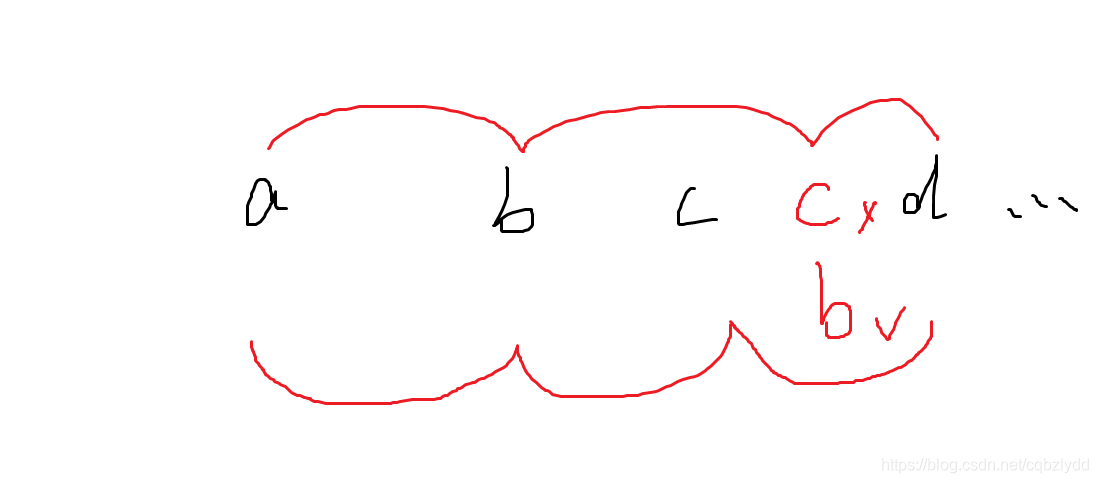
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn) 。
其实这道题我最开始的想法是考虑 26 26 26 种颜色,也能保证字符串长得不一样,但是似乎很难算答案。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mx=2e6+5;
const int mod=1e9+7;
int n,m;
ll res,fac[mx],inv[mx];
//相同的字符 x ,取序列中的最后一个
ll fpow(ll x,ll y) {
ll mul=1;
for(;y;y>>=1) {
if(y&1) mul=mul*x%mod;
x=x*x%mod;
}
return mul;
}
ll C(ll x,ll y) {
return fac[x]*inv[x-y]%mod*inv[y]%mod;
}
ll A(ll x,ll y) {
return fac[x]*inv[y]%mod;
}
ll G(ll x,ll y) {
return C(x+y-1,y-1);
}
char s[mx];
int main() {
// freopen("data.in","r",stdin);
scanf("%d%s",&m,s+1),n=strlen(s+1);
fac[0]=1;
for(int i=1;i<=2000000;i++) fac[i]=fac[i-1]*i%mod;
inv[2000000]=fpow(fac[2000000],mod-2);
for(int i=2000000;i>=1;i--) {
inv[i-1]=inv[i]*i%mod;
}
for(int i=1;i<=m+1;i++) {
ll turn1=fpow(26,i-1),turn2=C(n+m-i,n-1)*fpow(25,n+m-i-(n-1))%mod;
res=(res+turn1*turn2%mod)%mod;
}
cout<<res;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号