【题解】ABC 211

前言

主要讲一下 F 题。E 题是一个爆搜，模拟连通块用 map 去重即可。

F - Rectilinear Polygons

首先看到题意是比较晕的。

考虑 m=4 的情况，可以离散化排序 x 坐标，用树状数组维护即可。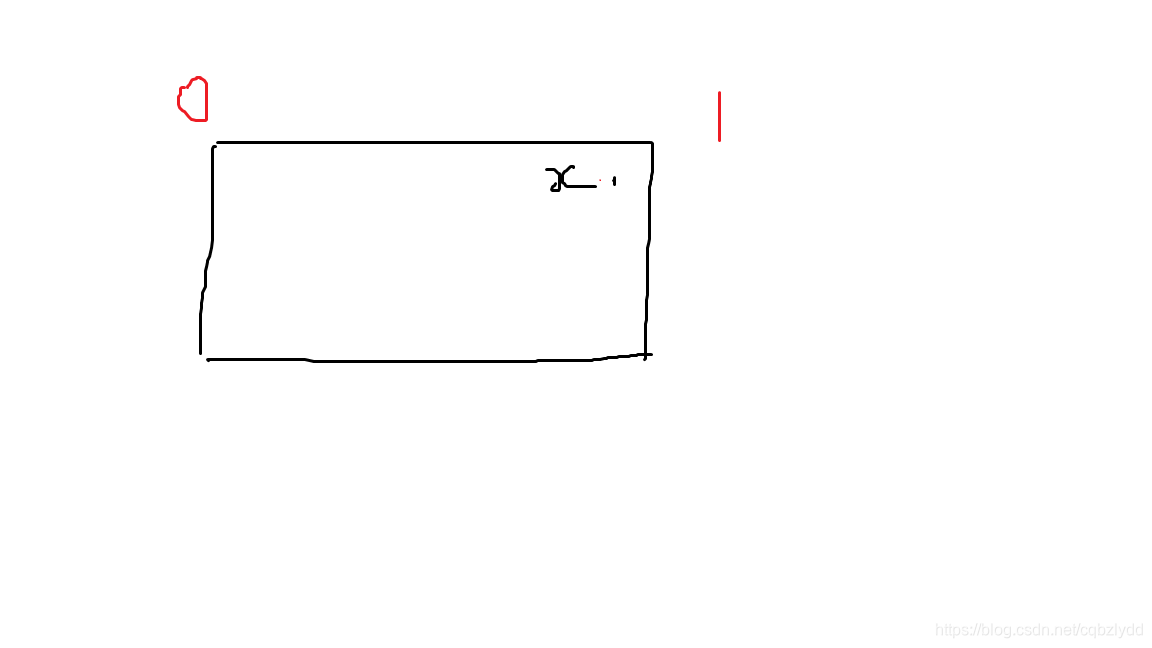
多边形就不会了 qwq 。能不能也用树状数组完成区间修改呢？

来看这个图，我们 坚定地只看平行于 y 轴的线段 ，观察发现可以按奇偶性讨论，讨论相邻块之间夹的部分是否在矩形内。

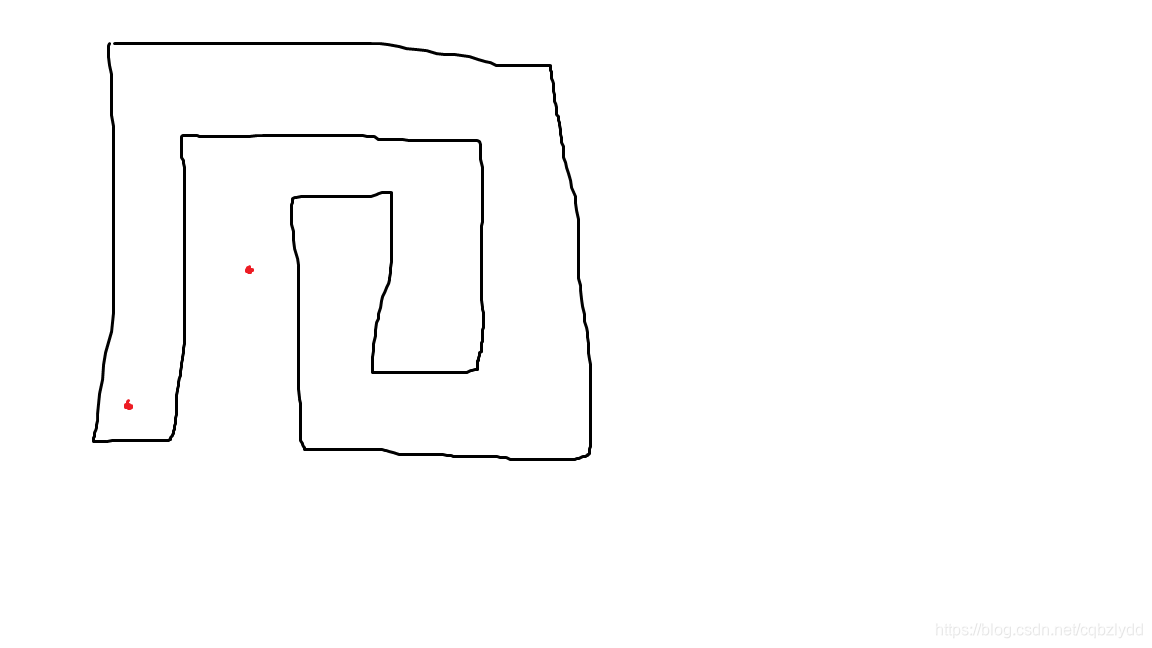
现在我们 只看相邻线段的前一项 。分类讨论：

1. 若 i%2==0 ，说明 [l,r] 对应为空， update(l,-1) + update(r,1)
2. 若 i%2==1 ，说明 [l,r] 在矩形内， update(l,1) + update(r,-1)

顺便说一下，这里要把 平行于 y 轴的线段 和询问的点离线在一起跑。

时间复杂度 O(nlogn) 。

代码比较冗。。。

#include<bits/stdc++.h>
#define fi first
#define se second
#define ll long long
#define PII pair<int,int>
#define All(x) x.begin(),x.end()
using namespace std;
const int mx=1e6+5;
int n,m,k,lsh[mx],cnt;
int bit[mx],ans[mx];
PII A[mx];
vector<PII> C[mx],D[mx];
void update(int x,int k) {
//	cout<<x<<endl;
	for(int i=x;i<=1e5+1;i+=i&-i) bit[i]+=k;
}
int query(int x) {
//	cout<<x<<endl;
	int tot=0;
	for(int i=x;i;i-=i&-i) tot+=bit[i];
	return tot;
}
int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		scanf("%d",&k);
		int it=0;
		for(int j=0;j<k;j++) {
			int x,y; scanf("%d%d",&x,&y); x++,y++;
			lsh[j]=x; A[j]=make_pair(x,y);
			if(A[j]<A[it]) it=j;
		}
        int f=1;
        for(int j=0;j<k;j++) {
        	C[A[(it+j)%k].first].push_back(make_pair(A[(it+j)%k].second,f));
        	f*=-1;
		}
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++) {
		int x,y; scanf("%d%d",&x,&y); x++,y++;
	    D[x].push_back(make_pair(y,i));
	}
	
	for(int i=1;i<=1e5+1;i++) {
		for(auto t:C[i]) {
			int l=t.fi,x=t.se;
			update(l,x);
		} 
		for(auto t:D[i]) {
			int x=t.fi,y=t.se;
			ans[y]=query(x);
		}
	}
	for(int i=1;i<=m;i++) printf("%d\n",ans[i]); //bye bye
}

__EOF__

本文作者：仰望星空的蚂蚁
本文链接：https://www.cnblogs.com/cqbzly/p/17530314.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！