【题解】[POI2005] SZA-Template

题意

给你一个长度为 n 的字符串，求印章长度的最小值，这个印章可以重复印刷同一个位置，但是每次必须恰好把所有字母都印到纸上。n<=5e5。

Solution:

考点：字符串匹配。

以为是水题，结果是神题。。。

$kczno1$ 是用 双向链表 + fail 指针 做的。然而我们有更简洁的做法。来自于 $PeterZ$ 。

设 f[i] 表示前缀为 i 的模板长度的最小值。

引理1:f[i] 的取值只能为 i 或 f[nxt[i]]

引理1.1:f[i]<=i

引理1.2:f[i]>=f[nxt[i]]。假如 f[i] 不能覆盖 nxt[i] ，说明 i 存在更大的 border ，与 nxt[i] 矛盾

引理1.3:若 f[i]<i ,则 f[i]<=nxt[i] 。因为 f[i] 同样是 border ,所以肯定小于等于 nxt[i]

引理1.4:若 f[i]<nxt[i],则 f[i]=f[nxt[i]] 。假如 f[nxt[i]]<f[i]<nxt[i] ，那么由定义可知，f[i] 可以覆盖 i, f[nxt[i]] 可以覆盖 nxt[i] ,所以 f[nxt[i]] 可以覆盖 f[i] (因为 f[i]<nxt[i]) ,与 f[i] 是最小的能覆盖 i 的模板矛盾

引理1.5:若 f[i]=nxt[i], 则 f[nxt[i]]=nxt[i] 即 f[i]=f[nxt[i]] 。假如 f[nxt[i]]<nxt[i], 那么 f[nxt[i]] 可以覆盖 nxt[i] ，同时 nxt[i] 可以覆盖 i, 所以 f[i]=f[nxt[i]]<nxt[i] ，矛盾

综上，由 引理1.4-5 知 f[i]=f[nxt[i]] 。故 引理1 成立。

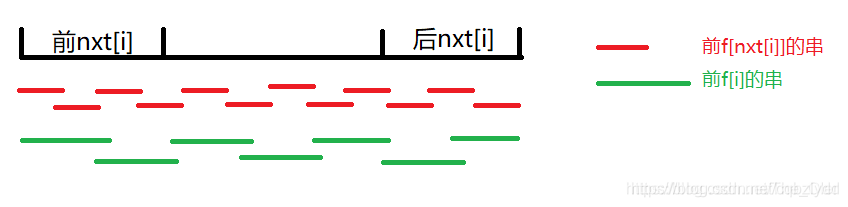
引理2:f[i]=f[nxt[i]] <=> 存在 j∈[i−nxt[i],i)，f[j]=f[nxt[i]]

先证充分性。在 [i-nxt[i],i) 任选一点 j ，不难证明总能找到一个 f[j]=f[nxt[i]] 。

再证必要性。根据定义， f[nxt[i]] 能覆盖 nxt[i] ，所以 (i-nxt[i],i] 也能被 f[nxt[i]] 覆盖，同时 f[j]=f[nxt[i]] 所以 f[nxt[i]] 能覆盖 [1,j] , 又因为 j∈[i−nxt[i],i) ，所以 f[nxt[i]] 能覆盖 i 。

综上，我们只需要判断 f[nxt[i]] 出现的位置 >=i-nxt[i] 即可，则 f[i]=f[nxt[i]] ，否则 f[i]=i 。

时间复杂度 O(n) 。是字符串分类讨论的好题。

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
const int N=1e6+5;
char a[N],b[N];
int n,nxt[N],minn[N];
int q[N];
void Kmp() {
	nxt[1]=0; minn[1]=q[1]=1;
	for(int i=2,j=0;i<=n;i++) {
		while(j>0&&a[i]!=a[j+1]) j=nxt[j];
		if(a[i]==a[j+1]) j++;
		nxt[i]=j; minn[i]=i;
		if(q[minn[nxt[i]]]>=i-minn[nxt[i]]) minn[i]=minn[nxt[i]]; 
		q[minn[i]]=i;
	}
}
int main() {
	scanf("%s",a+1);
	n=strlen(a+1);
	Kmp(); 
	printf("%d",minn[n]);
}

这个结论好神。。。