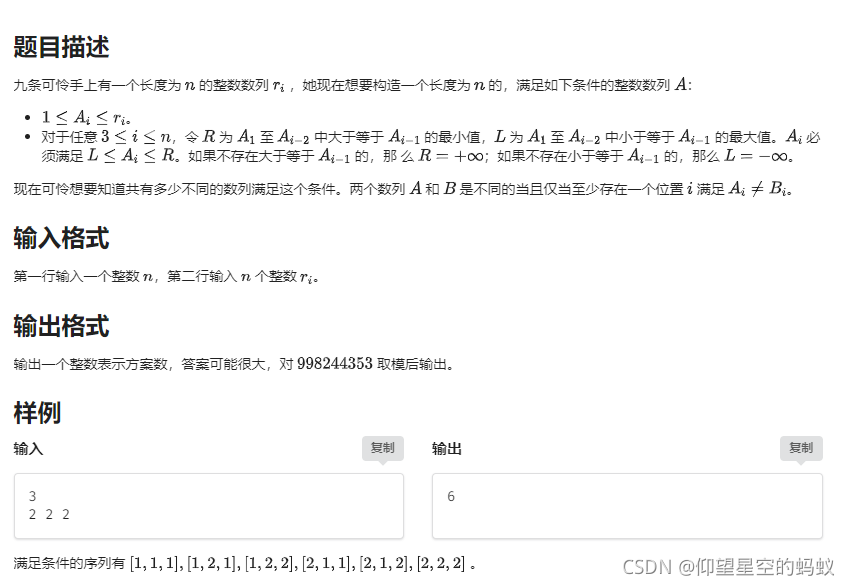
【题解】[JXOI2017] 数列

sol：

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
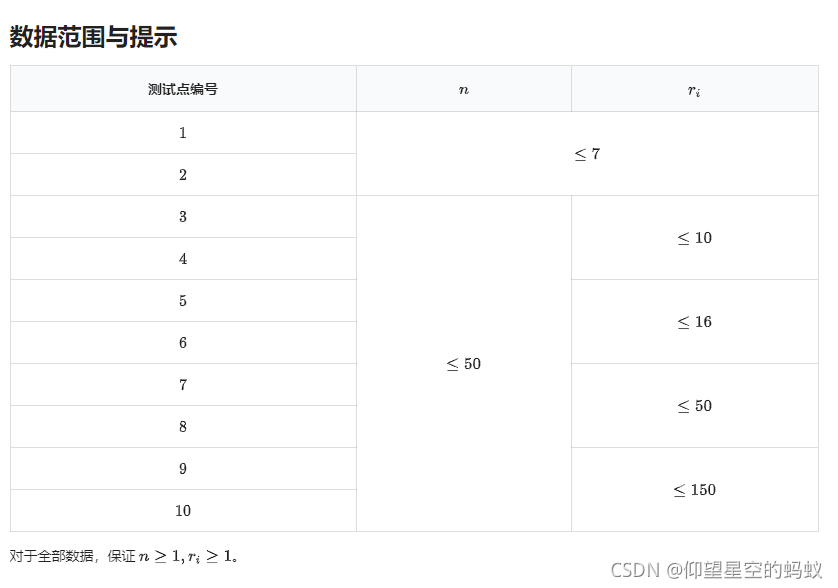
//诡异的数据范围
//观察可以发现 r_i 的数据范围很小，所以可以想到状压
//dp[i][j][s] 表示当前考虑了前 i 个数，第 i 个数为 j ，s 表示 1~s_i 中出现了哪些数 
//时间复杂度 o(2^s_i * n) 
//考虑怎么优化这个 dp (如，只关注转移最大值，最小值等) 
//在从这个方面深入之前，我们先举一些例子加深理解
//3 2 4 1 5
//在 (a_i,a_{i-1}] 之间有数，所以 a_4 不满足条件
//在 [a_{i-1},a_i) 之间有数，所以 a_5 不满足条件
//想一想逆推
//事实上这个限制区间是可以写成 [l,r] 的
//设 dp[i][j][k] 表示考虑了前 i 个数，其中最小值为 j, 最大值为 k 的方案数
//dp[i][j][k] = ∑dp[i-1][j'][k']  
const int N=55;
const int M=155;
const int mod=998244353;
int n,m,a[N],dp[N][M][M];
void add(int &x,int y) {
	x=(x+y)%mod;
}
int bi(int sta,int x) {
	for(int i=x;i<=m;i++) {
		if(sta>>i&1) return i;
	}
	return inf;
}
int sm(int sta,int x) {
	for(int i=x;i>=0;i--) {
		if(sta>>i&1) return i;
	}
	return -inf;
}
int dfs(int n,int l,int r) {
	if(n==0) return 1;
	if(dp[n][l][r]!=-1) return dp[n][l][r];
	int ans=0;
	if(l==0) {
		for(int i=1;i<=a[n];i++) {
			if(i==r) add(ans,dfs(n-1,l,r));
			else if(i>r) add(ans,dfs(n-1,r+1,i));
			else if(i<r) add(ans,dfs(n-1,i,r-1));
		}
	}
	else {
		for(int i=1;i<=a[n];i++) {
			if(l<=i&&i<=r) continue;
			if(i<l) add(ans,dfs(n-1,i,r));
			else add(ans,dfs(n-1,l,i));
		}
	}
	return dp[n][l][r]=ans;
}
int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		scanf("%d",&a[i]);
	}
	if(n<=2) {
		int res=1;
		for(int i=1;i<=n;i++) {
			res*=a[i];
		}
		printf("%d",res);
		return 0;
	}
	memset(dp,-1,sizeof dp);
	int ans=0;
	for(int i=1;i<=a[n];i++) {
		add(ans,dfs(n-1,0,i));
	}
	printf("%d",ans);
}

总结：本题主要考察对 dp 限制的转化，利用了逆向思维，简化了 dp 状态。

__EOF__

本文作者：仰望星空的蚂蚁
本文链接：https://www.cnblogs.com/cqbzly/p/17530214.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！