「AT_diverta2019_2_e」Balanced Piles 题解

题意描述

有一个长度为 \(N(2\le N \le 10^6)\) 的数组，一开始所有元素均为 \(0\)。
设 \(M\) 为当前数组中的最大元素，\(m\) 是当前数组中的最小元素，你可以执行若干次以下操作：

• 选择一个大小为 \(m\) 的元素，把他变为 \(x\)，其中 \(M\le x \le M+D\) 且 \(m<x\)。
  求有多少种操作方法使得数组中的所有元素均为 \(H\)，对 \(10^9+7\) 取模。
  \(1\le D\le H\le10^6\)。

题解

本题是一道十分 NB 的提前计算题。发现不好记录最小元素的状态，我们转而考虑记录最大元素的。定义 \(dp(x,y)\) 表示当前最大元素为 \(x\)，最大元素数量为 \(y\)。尽管我们记录的是最大元素，但它总会在后面变成最小元素，我们只要现在将贡献统计就好了。而最小元素的贡献实际上就是它的排列数（即我们取它的方案数）。转移见下图即可明了：

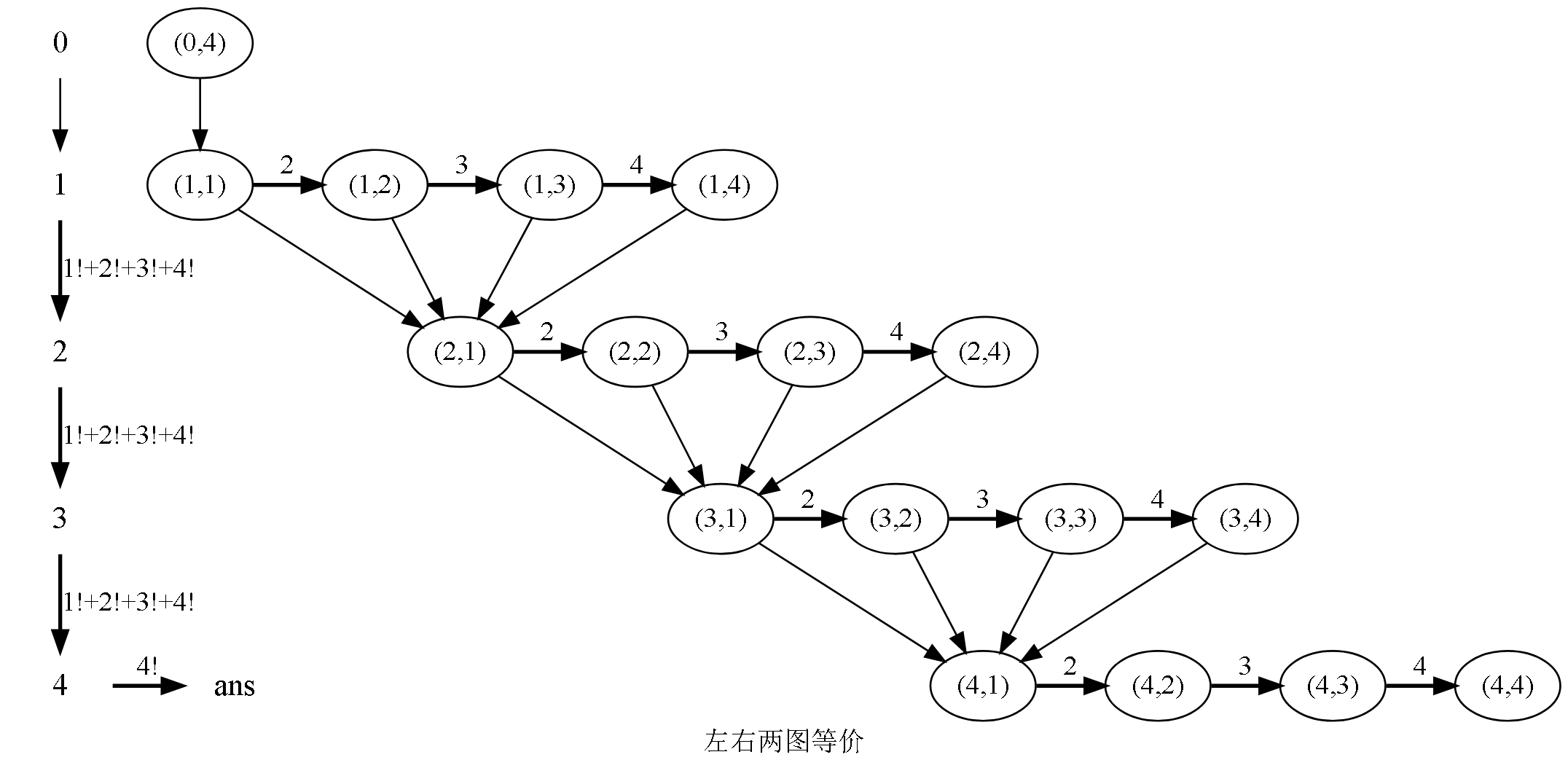
\(N=4,H=4,D=1\) 时，方案数等价于以下图的 \((0,4)→(4,4)\) 的路径条数：

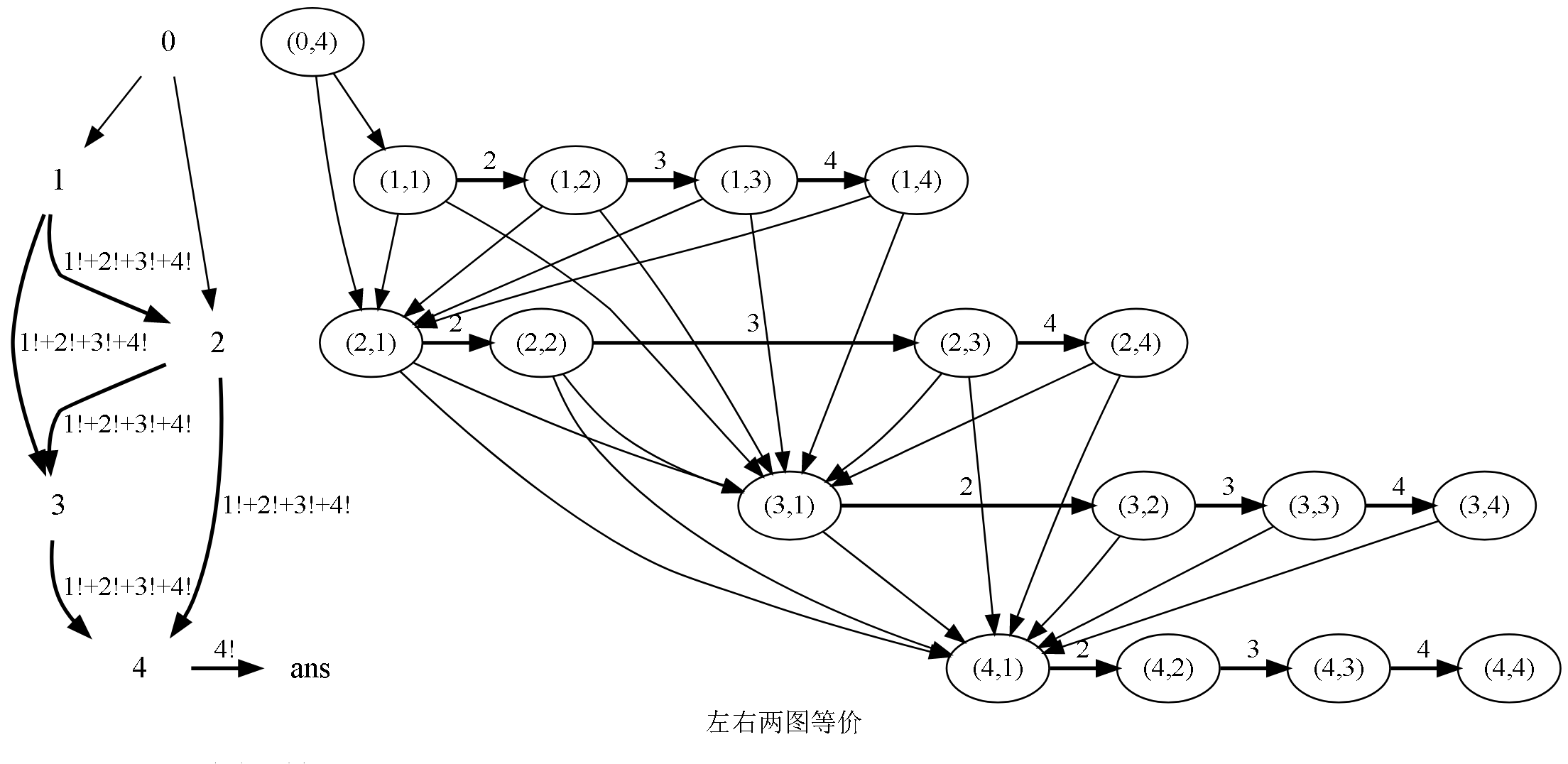
\(N=4,H=4,D=2\) 时，方案数等价于以下图的 \((0,4)→(4,4)\) 的路径条数：

直接转移即可。时间复杂度 \(\mathcal O(n)\)。

代码

#include <bits/stdc++.h>
using namespace std;

using ci = const int;

using u32 = uint32_t;
using i64 =  int64_t;
using u64 = uint64_t;

const int mod = 1e9 + 7;

constexpr inline int dil(int x) { return x >> 31 ? x + mod : x; }

struct Module {
	using cm = const Module;

	int v;

	constexpr Module() : v() {}
	constexpr Module(int _v) : v(_v) {}

	friend constexpr Module operator+(cm &x, cm &y) {
		return dil(x.v + y.v - mod);
	}
	friend constexpr Module operator-(cm &x, cm &y) {
		return dil(x.v - y.v);
	}
	friend constexpr Module operator*(cm &x, cm &y) {
		return static_cast<u64>(x.v) * static_cast<u64>(y.v) % mod;
	}

	constexpr void operator+=(cm &o) { *this = *this + o; }
	constexpr void operator-=(cm &o) { *this = *this - o; }
	constexpr void operator*=(cm &o) { *this = *this * o; }
};

const int N = 1e6 + 5;

int n, d, h;
Module fct[N], f[N];

int main() {
#ifdef LOCAL
	freopen(".in", "r", stdin);
	freopen(".out", "w", stdout);
#endif

	cin >> n >> h >> d;
	fct[0] = 1;
	for (int i = 1; i <= n; ++i) fct[i] = fct[i - 1] * i;
	f[0] = 1;
	Module sum = 0, tot = 1;
	for (int i = 1; i <= n; ++i) sum += fct[i];
	for (int i = 1; i <= h; ++i) {
		tot += (f[i] = tot) * sum;
		if (i >= d) tot -= f[i - d] * (i == d ? 1 : sum);
	}
	cout << (fct[n] * f[h]).v;

	return 0;
}

参考链接

https://www.cnblogs.com/frank3215/p/diverta2019-2E.html （图片也是这里贺的）