分拆数

更新日志

点击查看日志

• 2023-08-10 21:35:48 星期四 将大体板块搬运+修改了一下

分拆： 将自然数 \(n\) 写成递降正整数和的表示。

\[n=r_1+r_2+\ldots+r_k \quad (r_1 \ge r_2 \ge \ldots \ge r_k \ge 1) \]

和式中每个正整数称为一个部分。

分拆数：\(p_n\)。自然数 \(n\) 的分拆方法数。

自 0 开始的分拆数：

n	0	1	2	3	4	5	6	7	8
\(p_n\)	1	1	2	3	5	7	11	15	22

k 部分拆数

将 \(n\) 分成恰有 \(k\) 个部分的分拆，称为 \(k\) 部分拆数，记作 \(p(n,k)\)。
显然，\(k\) 部分拆数 \(p(n,k)\) 同时也是下面方程的解数：

\[n-k=y_1+y_2+\ldots+y_k\quad (y_1\ge y_2\ge\ldots\ge y_k\ge 0) \]

发现 \(p(n,k)\) 可以由以下两部分贡献：

1. 可以增加一个 \(1\) 的部分；
2. 可以把之前所有的部分加 \(1\)。

因此有和式：

\[p(n,k)=p(n-1,k-1)+p(n-k,k) \]

如果列出表格，每个格里的数，等于左上方的数，加上该格向上方数，所在列数个格子中的数。

生成函数

由等比数列求和公式，有：

\[\dfrac{1}{1-x^k}=1 + x^k + x^{2k}+\dots \]

所以

\[G(x)=\dfrac{1}{1-x}\dfrac{1}{1-x^2}\dfrac{1}{1-x^3}\dots \]

对于 k 部分拆数，生成函数稍微复杂。具体写出如下：

\[\sum_{n,k=0}^\infty {p(n,k) x^n y^k }=\frac{1}{1-xy} \frac{1}{1-x^2 y} \frac{1}{1-x^3y}\dots \]

Ferrers 图

Ferrers 图： 将分拆的每个部分用点组成的行表示。每行点的个数为这个部分的大小。

根据分拆的定义，Ferrers 图中不同的行按照递减的次序排放。最长行在最上面。
例如：分拆 12=5+4+2+1 的 Ferrers 图。

将一个 Ferrers 图沿着对角线翻转，得到的新 Ferrers 图称为原图的共轭，新分拆称为原分拆的共轭。显然，共轭是对称的关系。
例如上述分拆 \(12=5+4+2+1\) 的共轭是分拆 \(12=4+3+2+2+1\)。

最大 \(k\) 分拆数： 自然数 \(n\) 的最大部分为 \(k\) 的分拆个数。

根据共轭的定义，有显然结论：
最大 \(k\) 分拆数与 \(k\) 部分拆数相同，均为 \(p(n,k)\)。

互异分拆数

互异分拆数：\(pd_n\)。自然数 n 的各部分互不相同的分拆方法数。（Different）

n	0	1	2	3	4	5	6	7	8
\(pd_n\)	1	1	1	2	2	3	4	5	6

同样地，定义互异 \(k\) 部分拆数 \(pd(n,k)\)，表示最大拆出 \(k\) 个部分的互异分拆，是这个方程的解数：

\[n=r_1+r_2+\ldots+r_k\quad (r_1>r_2>\ldots>r_k\ge 1) \]

完全同上，也是这个方程的解数：

\[n-k=y_1+y_2+\ldots+y_k\quad (y_1>y_2>\ldots>y_k\ge 0) \]

这里与上面不同的是，由于互异，新方程中至多只有一个部分为零。有不变的结论：恰有 \(j\) 个部分非 \(0\)，则恰有 \(pd(n-k,j)\) 个解，这里 \(j\) 只能取到 \(k\) 或 \(k-1\)。因此直接得到递推：

\[pd(n,k)=pd(n-k,k-1)+pd(n-k,k) \]

同样像组合数一样列出表格，每个格里的数，等于该格前一列上数，所在列数个格子中的数，加上该格向上方数，所在列数个格子中的数。

生成函数

由于每个值最多只能取一个，所以：

\[G(x)=(1+x)(1+x^2)(1+x^3)\dots \]

奇分拆数

奇分拆数：\(po_n\)。自然数 \(n\) 的各部分都是奇数的分拆方法数。（Odd）
有一个显然的等式：（从奇偶性上来分析）

\[\prod_{i=1}^\infty (1+x^i ) =\frac{\prod_{i=1}^\infty (1-x^{2i} ) }{\prod_{i=1}^\infty (1-x^i ) }=\prod_{i=1}^\infty \frac{1}{1-x^{2i-1} } \]

最左边是互异分拆数的生成函数，最右边是奇分拆数的生成函数。两者对应系数相同，因此，奇分拆数和互异分拆数相同：

\[po_n=pd_n \]

但显然 \(k\) 部奇分拆数和互异 \(k\) 部分拆数不是一个概念，这里就不列出了。

再引入两个概念：
互异偶分拆数：\(pde_n\)。自然数 n 的部分数为偶数的互异分拆方法数。（Even）
互异奇分拆数：\(pdo_n\)。自然数 n 的部分数为奇数的互异分拆方法数。（Odd）
因此有：

\[pd_n=pde_n+pdo_n \]

同样也有相应的 \(k\) 部概念。由于过于复杂，不再列出。

五边形数定理

单独观察分拆数的生成函数的分母部分：

\[\prod_{i=1}^\infty (1-x^i ) \]

将这部分展开，可以想到互异分拆，与互异分拆拆出的部分数奇偶性有关。

具体地，互异偶部分拆在展开式中被正向计数，互异奇部分拆在展开式中被负向计数。因此展开式中各项系数为两方法数之差。即：

\[\sum_{i=0}^\infty ({pde}_i-{pdo}_i ) x^i =\prod_{i=1}^\infty (1-x^i ) \]

接下来说明，多数情况下，上述两方法数相等，在展开式中系数为 \(0\)；仅在少数位置，两方法数相差 \(1\) 或 \(-1\)。

这里可以借助构造对应的办法。
画出每个互异分拆的 Ferrers 图。最后一行称为这个图的底，底上点的个数记为 \(b\) (Bottom)；连接最上面一行的最后一个点与图中某点的最长 \(45\) 度角线段，称为这个图的坡，坡上点的个数记为 \(s\) (Slide)。

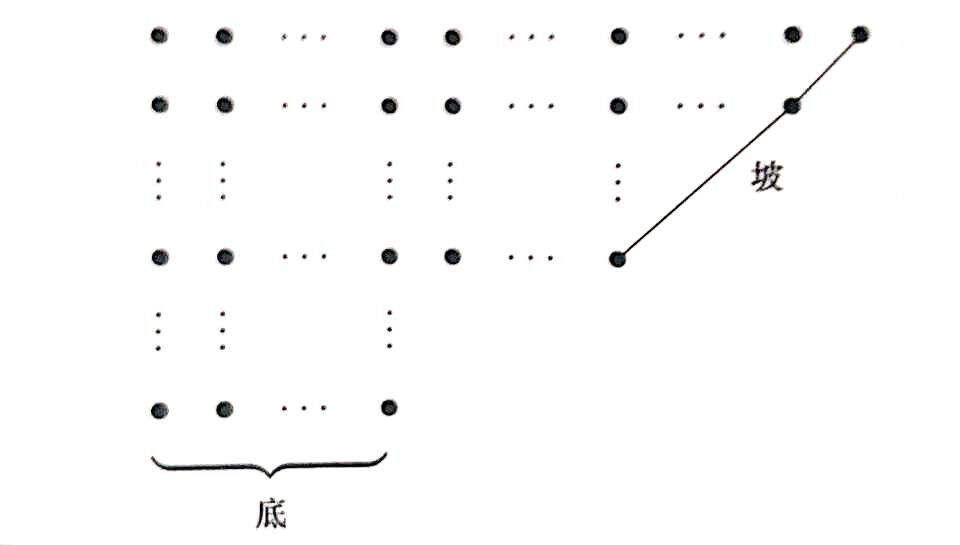
要想在互异偶部分拆与互异奇部分拆之间构造对应，就要定义变换，在保证互异条件不变的前提下，使得行数改变 \(1\)：

• 变换 A： 当 \(b\) 小于等于 \(s\) 的时候，就将底移到右边，成为一个新坡。
• 变换 B： 当 \(b\) 大于 \(s\) 的时候，就将坡移到下边，成为一个新底。

这两个变换，对于多数时候的 \(n\)，恰有一个变换可以进行，就在互异偶部分拆与互异奇部分拆之间构造了一个一一对应。已经构造了一一对应的两部分分拆个数相等，因此这时展开式中第 \(n\) 项系数为 \(0\)。
变换 A 不能进行的条件：底与坡有一个公共点，即 \(b=s\)。这种情形只发生于：

\[n=b+(b+1)+\ldots+(b+b-1)=b+\dfrac{b(b-1)}{2}=\dfrac{b(3b-1)}{2} \]

这时，展开式中第 \(n\) 项为：

\[\prod_{i=0}^{b-1} (-x)^{b+i} =(-1)^b \prod_{i=0}^{b-1} x^{b+i} =(-1)^b x^n \]

变换 B 不能进行的条件：底与坡有一个公共点，即 \(b=s+1\)。这种情形只发生于：

\[n=(s+1)+(s+2)+\ldots+(s+s)=\frac{s(3s-1)}{2} \]

这时，展开式中第 \(n\) 项为：

\[\prod_{i=1}^s (-x)^{s+i} =(-1)^s \prod_{i=1}^s x^{s+i} =(-1)^s x^n \]

至此，我们就证明了：

\[(1-x)(1-x^2 )(1-x^3 )…=\ldots+x^{26}-x^{15}+x^7-x^2+1-x+x^5-x^{12}+x^{22}-…=\sum_{k=-\infty}^{+\infty} (-1)^k x^{\frac{k(3k-1)}{2}} \]

将这个式子整理，对比两边各项系数，就得到递推式。

\[(1+p_1 x+p_2 x^2+p_3 x^3+\ldots)(1-x-x^2+x^5+x^7-x^{12}-x^{15}+x^{22}+x^{26}-…)=1 \]

\[p_n=p_{n-1}+p_{n-2}-p_{n-5}-p_{n-7}+\ldots \]

这个递推式有无限项，但是如果规定负数的分拆数是 \(0\)（\(0\) 的分拆数已经定义为 \(1\)），那么就简化为了有限项。