Summary Dec 6th 2025

Hotel

奶牛们正北上加拿大雷湾进行文化之旅，准备在苏必利尔湖阳光明媚的湖畔享受假期。作为称职的旅行代理，贝茜将著名的坎伯兰街公牛麋鹿酒店定为它们的下榻之处。这座巨型酒店拥有N间客房（1 ≤ N ≤ 50,000），所有房间都位于一条极长走廊的同一侧（当然是为了更好地欣赏湖景）。

奶牛和其他旅客以Di（1 ≤ Di ≤ N）为团体规模抵达前台办理入住。每个团体i会向当值的麋鹿管理员坎穆申请Di间连续客房。若有可用连续房间，坎穆会分配房号r至r+Di-1的序列；若无可用连续房间，则会礼貌推荐其他住宿。坎穆总是尽可能选择最小的r值。

旅客也会以连续房间为单位退房。每次退房请求包含参数Xi和Di，表示腾空Xi至Xi+Di-1号房间（1 ≤ Xi ≤ N-Di+1）。这些房间在退房前可能部分或全部本就空置。

你的任务是协助坎穆处理M次（1 ≤ M < 50,000）入住/退房请求。酒店初始处于全空状态。

输入格式

* 第1行：两个空格分隔的整数：N和M
* 第2..M+1行：第i+1行包含以下两种格式之一的请求：

(a) 两个空格分隔的整数表示入住请求：1和Di

(b) 三个空格分隔的整数表示退房请求：2、Xi和Di

输出格式

* 第1...行：对每个入住请求，输出一行整数r表示分配到的连续房间起始房号。若无法满足请求，则输出0。

总结就是两个操作：

a. query ： \(D_i\) ，找到最小的 r 使得 \([\text r, \text r + D_i-1]\) 是一段连续的 \(0\) (\(0\) 表示没住住人，\(1\) 表示住了人)

b.update ：\(x_i, D_i\)，将区间 \([\text x_i, \text x_i + D_i - 1]\) 清空

思路

首先想到的就是用线段树维护区间和，但是呢，这样子 query 的复杂度就变成了 \(\Omicron(\textcolor{red}n\log_2n)\) (单次)

再一看，既然是区间，那就不难想到一个经典做法：

struct node{
	int l, r;
} tree[maxn << 2];

其中 l 存储从该区间左侧开始的最长的连续 \(0\) 的长度，r 同理

那么判断条件就是当 tree[ls(id)].r + tree[rs(id)].l >= D_i 时 mid - tree[ls(id)].r + 1 就是答案

如图：

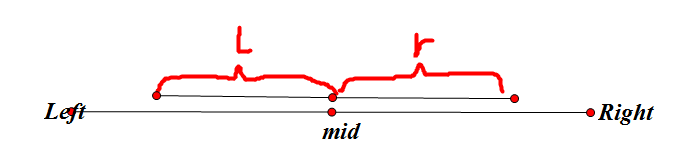
Dec 6th 8

还有一个小小的可行性剪枝：当 (r - l + 1) < D_i 时就没有必要往下搜索了

当然了，仅凭一个 l 和 r 是不行的，我们还需要存下整个区间的连续 \(0\) 的个数

struct node{
    int l, r, sum;
} tree[maxn << 2];

现在就又有了一个优化：当 tree[id].sum < D_i 时，也没有必要往下搜索了，但是没用

初始化：

tree[id].sum = tree[id].l = tree[id].r = right - left + 1; // 最开始都是 0 初始值就是它们的长度

现在就考虑maitain(pushup) update 和 pushdown 怎么写

首先 lazy_tag 的初始值应该是 \(-1\) ，\(0\) 表示要改 ~~好像也不用赋成-1~~(骗你的其实必须要赋值)

pushdown 的时候默认左右子节点继承父节点的 lazy_tag

void pushdown(ll id, ll left, ll right) {
    if (lazy_tag[id] != -1) {
        lazy_tag[ls(id)] = lazy_tag[rs(id)] = lazy_tag[id];
        // .....
    }
}

而当 lazy_tag[id] == 0 时，说明这个区间需要修改，改成 \(0\)

void pushdown(ll id, ll left, ll right) {
    if (lazy_tag[id] != -1) {
        lazy_tag[ls(id)] = lazy_tag[rs(id)] = lazy_tag[id];
        if (lazy_tag[id] == 1) {
            tree[ls(id)].l = tree[ls(id)].r = tree[ls(id)].sum = 0;
            tree[rs(id)].l = tree[rs(id)].r = tree[rs(id)].sum = 0;
        } else {
            tree[ls(id)].l = tree[ls(id)].r = tree[ls(id)].sum = (right - left + 1) - (right - left + 1) >> 1;
            tree[rs(id)].l = tree[rs(id)].r = tree[rs(id)].sum = (right - left + 1) >> 1;
        }
        lazy_tag[id] = -1;
    }
}

现在就考虑如何去写 maitain

void maitain(ll id) {
    tree[id].l = tree[ls(id)].l;
    tree[id].r = tree[rs(id)].r;
    // ....
}

这仅仅是最简单的继承

考虑如下情况：

\(\alpha\)，左区间的连续 \(0\) 区间包含了左区间

\(\beta\)，右区间同理

然后就是 sum 的更新

tree[id].sum = max({tree[id].sum, tree[ls(id)].sum, tree[rs(id)].sum, tree[ls(id)].r + tree[rs(id)].l})

void maitain(ll id, ll left, ll right) {
    tree[id].l = tree[ls(id)].l;
    tree[id].r = tree[rs(id)].r;
    ll len = (right - left + 1);
    if (tree[ls(id)].l == len - (len >> 1)) tree[id].l += tree[rs(id)].l;
    if (tree[rs(id)].r == len >> 1) 	    tree[id].r += tree[ls(id)].r;
    tree[id].sum = max({tree[id].sum, tree[ls(id)].sum, tree[rs(id)].sum, tree[ls(id)].r + tree[rs(id)].l});
}

update 应该是最简单的一个：

void update(ll L, ll R, ll id, ll left, ll right, ll num) {
	if (L <= left and right <= R) {
		if (num == 0)
			tree[id].l = tree[id].r = tree[id].sum = (right - left + 1);
		else
			tree[id].l = tree[id].r = tree[id].sum = 0;
		lazy_tag[id] = num;
		return ;
	}
	
	pushdown(id, left, right);
	ll mid = (left + right) >> 1;
	if (L <= mid) update(L, R, ls(id), left, mid, num);
	if (R > mid)  update(L, R, rs(id), mid + 1, right, num);
	maitain(id, left, right);
}

最后的最后呢

就是 query 了

其实很好写，根据我们之前的分析的话

ll query(ll id, ll left, ll right, ll d) {
	if (left == right) return left;
	pushdown(id, left, right);
	ll mid = (left + right) >> 1;
	if (tree[ls(id)].sum >= d)                     return query(ls(id), left, mid, d);
	else if (tree[ls(id)].r + tree[rs(id)].l >= d) return mid - tree[ls(id)].r + 1;
	else if (tree[rs(id)].sum >= d)                return query(rs(id), mid + 1, right, d);
	return 0;
}

~~劳版本c++还是太强了，交了7次，7次都是CE~~

#include <iostream>
#include <algorithm>
using namespace std;

const int maxn = 5e5 + 5;

struct node {
	int l, r, sum;
} tree[maxn << 2];

int lazy_tag[maxn << 2];

long long ls(long long id) {return id << 1;}
long long rs(long long id) {return id << 1 | 1;}

void maitain(long long id, long long left, long long right) {
	long long mid = (left + right) >> 1;
	long long llen = mid - left + 1;
	long long rlen = right - mid;

	tree[id].l = tree[ls(id)].l;
	if (tree[ls(id)].l == llen)
		tree[id].l += tree[rs(id)].l;
	tree[id].r = tree[rs(id)].r;
	if (tree[rs(id)].r == rlen)
		tree[id].r += tree[ls(id)].r;

	tree[id].sum = max(max(tree[ls(id)].sum, tree[rs(id)].sum), tree[ls(id)].r + tree[rs(id)].l);
}

void pushdown(long long id, long long left, long long right) {
	if (lazy_tag[id] == -1) return;

	long long mid = (left + right) >> 1;
	long long llen = mid - left + 1;
	long long rlen = right - mid;

	lazy_tag[ls(id)] = lazy_tag[id];
	lazy_tag[rs(id)] = lazy_tag[id];

	if (lazy_tag[id] == 1) {
		tree[ls(id)].l = tree[ls(id)].r = tree[ls(id)].sum = 0;
		tree[rs(id)].l = tree[rs(id)].r = tree[rs(id)].sum = 0;
	} else {
		tree[ls(id)].l = tree[ls(id)].r = tree[ls(id)].sum = llen;
		tree[rs(id)].l = tree[rs(id)].r = tree[rs(id)].sum = rlen;
	}

	lazy_tag[id] = -1;

}

void build(long long id, long long left, long long right) {
	lazy_tag[id] = -1;
	if (left == right) {
		tree[id].l = tree[id].r = tree[id].sum = 1;
		return ;
	}
	long long mid = (left + right) >> 1;
	build(ls(id), left, mid);
	build(rs(id), mid + 1, right);
	maitain(id, left, right);
}

void update(long long L, long long R, long long id, long long left, long long right, long long num) {
	if (L <= left and right <= R) {
		if (num == 0)
			tree[id].l = tree[id].r = tree[id].sum = (right - left + 1);
		else
			tree[id].l = tree[id].r = tree[id].sum = 0;
		lazy_tag[id] = num;
		return ;
	}

	pushdown(id, left, right);
	long long mid = (left + right) >> 1;
	if (L <= mid) update(L, R, ls(id), left, mid, num);
	if (R > mid)  update(L, R, rs(id), mid + 1, right, num);
	maitain(id, left, right);
}

long long query(long long id, long long left, long long right, long long d) {
	if (left == right) return left;

	pushdown(id, left, right);
	long long mid = (left + right) >> 1;

	if (tree[ls(id)].sum >= d)
		return query(ls(id), left, mid, d);
	else if (tree[ls(id)].r + tree[rs(id)].l >= d)
		return mid - tree[ls(id)].r + 1;
	else if (tree[rs(id)].sum >= d)
		return query(rs(id), mid + 1, right, d);
	return 0;
}

void solve() {
//	cout << "hellow world\n";
	int n, m;
	cin >> n >> m;
	build(1, 1, n);
	while (m--) {
		int oper;
		cin >> oper;
		if (oper == 1) {
			int d;
			cin >> d;
			if (tree[1].sum < d) {
				cout << 0 << "\n";
				continue;
			}
			int p = query(1, 1, n, d);
			cout << p << "\n";
			update(p, p + d - 1, 1, 1, n, 1);
		} else {
			int x, d;
			cin >> x >> d;
			update(x, x + d - 1, 1, 1, n, 0);
		}
	}
}

int main() {

	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	//	freopen("T1.in", "r", stdin);
	//	freopen("T1.out", "w", stdout);

	int T = 1;
	//	cin >> T;
	while (T--) solve();

	return 0;
}

DZY Loves Colors

DZY喜欢颜色，他喜欢绘画。

在一个色彩斑斓的日子里，DZY得到了一根多彩的丝带，它由n个单位组成（它们从左到右编号为1到n）。丝带上第i个单位的颜色初始为i。它已经足够多彩了，但我们仍然认为每个单位的色彩丰富度初始为0。

DZY喜欢绘画，我们知道。他拿起一支颜色为x的画笔，用它在丝带上画了一条线。在这种情况下，一些相邻的单位被涂上了颜色。想象一下，单位i当前的颜色为y。当它被这支画笔涂上时，单位的颜色变为x，并且单位的色彩丰富度增加了|x - y|。

DZY想要进行m次操作，每个操作可以是以下之一：

用颜色x涂抹所有编号在l和r之间（包括两端）的单位。
询问编号在l和r之间（包括两端）的单位的色彩丰富度之和。

你能帮助DZY吗？

输入

第一行包含两个以空格分隔的整数n, m (1 ≤ n, m ≤ 105)。

接下来的每一行以整数type (1 ≤ type ≤ 2)开头，表示这个操作的类型。

如果type = 1，那么这一行将再有3个整数l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 108)，描述一个操作1。

如果type = 2，那么这一行将再有2个整数l, r (1 ≤ l ≤ r ≤ n)，描述一个操作2。

输出

对于每个操作2，输出一行包含答案 — 色彩丰富度之和。

示例1

Input	Output
`3 3 1 1 2 4 1 2 3 5 2 1 3`	`8`

示例2

Input	Output
`3 4 1 1 3 4 2 1 1 2 2 2 2 3 3`	`3 2 1`

示例3

Input	Output
`10 6 1 1 5 3 1 2 7 9 1 10 10 11 1 3 8 12 1 1 10 3 2 1 10`	`129`

注意

在第一个示例中，每个单位的颜色初始为[1, 2, 3]，色彩丰富度为[0, 0, 0]。

第一个操作后，颜色变为[4, 4, 3]，色彩丰富度变为[3, 2, 0]。

第二个操作后，颜色变为[4, 5, 5]，色彩丰富度变为[3, 3, 2]。

因此，唯一的类型为2的操作的答案是8。

~~上课上着上着睡着了~~

第一眼就是两个 lazy_tag 一个用于存储赋值的修改，另一个用于存储增加的修改

思考过程并不麻烦与复杂

时间复杂度的证明：

法1（聚合分析，Aggregate Analysis）

聚合分析（直接搬 OI-wiki 了）:

聚合分析（Aggregate Analysis）通过计算一系列操作的总成本，并将其平均到每次操作上，从而得出每次操作的均摊时间复杂度。

考虑总的复杂度 \(\text T(n)\) ，在进行 \(n\) 此操作后，\(\text T(n) = n\log_2 n+\frac12n\log_2n = \mathcal O(n\log_2n)\)

均摊则为：\(\text T'=\frac{\mathcal{O} (n\log_2n)}{n} = \mathcal{O}(\log_2n)\)

~~十份滴煎蛋~~

法2（势能分析，Potential Method）

势能分析

势能分析（Potential Method）通过定义一个势能函数（通常表示为 \(\Phi\)），度量数据结构的 潜在能量，即系统状态中的预留资源，这些资源可以用来支付未来的高成本操作。势能的变化用于平衡操作序列的总成本，从而确保整个算法的均摊成本在合理范围内。

观察 color 改变的过程，我们发现其过程和并查集十分的相像

考虑建模成并查集

所以单次操作就为 \(\mathcal O (\alpha(n)\log_2n)\)

当然，这仅仅是粗略的估计（毕竟没有启发式合并）

考虑证明：

将 color 看成并查集

定义 \(\Phi(S_i)\) 表示 \(S_i\) 的状态下 color 所含的势能

定义辅助函数，level 与 iter

level(x) ：\(\max\{y:2^{\text{level}(y)}\le\text{rank}_y\}\)

iter(x) ： \(\max\{x:\text{iter}(x) \le \text{level}(p(x))\}\)

则：

\[\Phi(x) = \begin{cases} \alpha(n) \cdot \text{rank}(x) &\text{rank}_x = 0 \ \ \lor \ \ \text{x是某棵树的根节点} \\ \alpha(n)\cdot \text{level}(x)+\text{iter}(x) &\text{if } \text{otherwise} \end{cases} \]

记：

\[\hat{c}_i=c_i+\Delta \Phi(i) \]

考虑 union 操作
union(x, y) 中尽可能 y 增加势能，最多增加 \(\Omicron(\alpha(n))\)

考虑 find 操作

posted @ 2025-12-06 10:52 Yangyihao 阅读(12) 评论(1) 收藏举报

刷新页面返回顶部

Yangyihao

Wir müssen wissen, wir werden wissen.

Summary Dec 6th 2025

Hotel

输入格式

输出格式

DZY Loves Colors

输入

输出

示例1

示例2

示例3

注意

公告