最小生成树(Minimum Spanning Tree)

最小生成树

最小生成树实在一个无向图内，找到一棵树，使得其包含其所有节点，且使得\(\sum w(u, v)\)最小

Kruskal

贪心思想，使用并查集维护树形结构
举个栗子

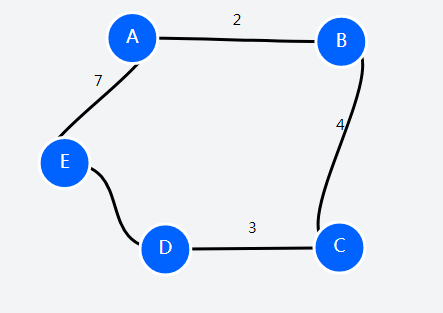
这是一个无向图

A -> B : 2
A -> E : 7
E -> D : 1
C -> D : 3
B -> C : 4

先按照边权排序

E -> D : 1
A -> B : 2
C -> D : 3
B -> C : 4
A -> E : 7

初始化并查集(fa[])

fa = {A : A, B :B, C : C, D : D, E : E}

初始化MST

MST = {}

对于节点E以及D
注意到

find(E) != find(D)

它们没有构成一个环
所以合并它们

union(E, D)

此时

fa{A : A, B : B, C : C, D : E, E : E}
MST = {D -> E, 1;}

重复此操作
我们会得到

MST = {D -> E, C -> D, B -> C, A -> B}

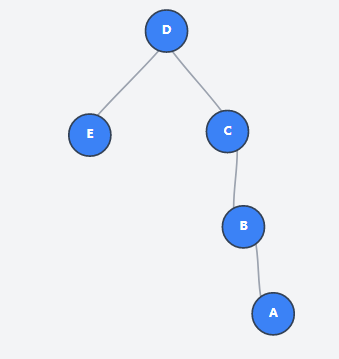
此时

\[\sum w(u, v) = 10 \]

可以证明其最小

Kruskal的正确性证明

我们需证明

• 生成的是一棵树
• 这棵树“最小”

首先证明这是一棵树

不难发现，我们使用并查集维护了树形结构
所以我们就需要证明其联通
初始时所有顶点都是独立的，每次添加边都会合并两个连通分量，最终所有顶点连通(因为原图是连通的)

其次，我们证明其是最优的

考虑\(T\)是由Kruskal算法生成的，而\(V\)是真正的最小生成树
接下来我们可证\(w(T) \le w(V)\)
考虑边\(e\)是Kruskal选择的第一条边，但其又不属于\(V\)
因为\(V\)是生成树，所以再加入\(e\)后，起变成一个环\(C\)
又由\(T\)中无环可知环\(C\)中存在一条边\(f \notin T\)
又因为Kruscal算法是按照边权从小到大选择的，易知\(w(e) \le w(f)\)
所以我们构造一棵生成树\(T' = V ∪ \{e\} - \{f\}\)
由\(w(e) \le w(f)\)知\(w(T') \le w(V)\)
重复操作，最后易知\(w(T) \le w(V)\)

代码实现

// 并查集实现
#include<bits/stdc++.h>
using namespace std;

class Disjoin_Set {
	private:
		vector<int> parent, rank;
	public:
		Disjoin_Set(int n) {
			parent.resize(n);
			rank.resize(n, 0);
			for (int i = 0; i < n; ++i)
				parent[i] = i;
		}
		int find(int x) {
			if (parent[x] != x)
				parent[x] = find(parent[x]);
			return parent[x];
		}
		void merge(int x, int y) { //按秩合并,O(α(n))
			int rootX = find(x);
			int rootY = find(y);
			if (rootX == rootY) return;
			if (rank[rootX] < rank[rootY])
				parent[rootX] = rootY;
			else {
				parent[rootY] = rootX;
				if (rank[rootX] == rank[rootY])
					rank[rootX]++;
			}
		}
		bool isConnected(int x, int y) {
			return find(x) == find(y);
		}
};
struct Edge {
	int u, v, weight;
	Edge(int u, int v, int w) : u(u), v(v), weight(w) {}
	bool operator<(const Edge& other) const {
		return weight < other.weight;
	}
};
vector<Edge> kruskal(int n, vector<Edge>& edges) {
	sort(edges.begin(), edges.end()); // 按照权值排序
	Disjoin_Set uf(n);
	vector<Edge> mst;
	for (const Edge& e : edges)
		if (!uf.isConnected(e.u, e.v)) {
			uf.merge(e.u, e.v);
			mst.push_back(e);
			if (mst.size() == size_t(n - 1)) break;
		}
	return mst;
}
int main() {
	return 0;
}

Prim算法