高等数学-2 导数与微分

函数连续性

定义1.1

(函数的连续)
设函数\(f(x)\)在\(x_0\)的领域\(U(x_0, \delta)\)内有定义，我们称\(f(x)\)在点\(x_0\)处连续(Continuous)，若\(\lim_{x \rightarrow x_0}f(x)\)存在，且\(\lim_{x \rightarrow x_0}f(x) = f(x_0)\)
我们称\(x_0\)为\(f(x)\)的连续点。
否则我们称函数\(f(x)\)在点\(x_0\)处间断(Discontinuous)，并称\(x_0\)为函数\(f(x)\)的间断点(A pointn of discontinuous)

定义1.2

(左右连续)
设函数\(f(x)\)定义在区间\([a, b]\)上，\(x_0 \in [a, b]\)。当\(x_0 \not= a\)时，若\(\lim_{x \rightarrow x_0^-} f(x) = f(x_0)\)，则称\(f(x)\)在点\(x_0\)处左连续(Left-continuous)；当\(x_0 \not= b\)时， 若\(\lim_{x \rightarrow x_0^+}f(x) = f(x_0)\)，则称\(f(x)\)在点\(x_0\)处右连续(Right-continuous)

定义1.3

(区间上的连续性)
我们称函数\(f(x)\)在开区间\((a, b)\)上连续，若函数\(f(x)\)在\((a, b)\)内每一点都连续；
我们称函数\(f(x)\)在闭区间\([a,b]\)上连续，若函数\(f(x)\)在\((a,b)\)上连续，且在断点处连续。
在定义域内每一点处都连续的函数称为连续函数(continuou functions)

连续函数的图像是一条连续且不间断的曲线
有理函数在其定义域内是连续的
多项式函数在\((-\infty, +\infty)\)上连续

定义1.4

间断点
无穷间断点(Infinity Discontinuity)：极限是无穷的点
可去间断点(Removale Discontinuity)：间断点两边极限存在
跳跃间断点(Jump Discontinuity)：间断点左右两边极限存在但是不相等
震荡间断点(Oscillating Discontinuity)：函数值震荡的间断点
我们也可以根据函数在间断点处的极限分为两类：
第一类间断点：若\(\lim_{x \rightarrow x_0^+}f(x)\)和\(\lim_{x \rightarrow x_0^-}f(x)\)都存在的间断点
第二类间断点：若\(\lim_{x \rightarrow x_0^+}f(x)\)和\(\lim_{x \rightarrow x_0^-}f(x)\)至少有一个不存在的间断点

初等函数的有理变换都是连续函数

定理1.1

(反函数的连续性)
若函数\(y = f(x)\)在区间\(I\)上是单调的连续函数，且其值域\(I'\)，那么其反函数\(y = f^{-1}(x)\)在\(I'\)上也是单调的连续函数

定理1.2

(复合函数的连续性)
若函数\(u = g(x)\)在点\(x_0\)处连续，且\(u_0 = g(x_0)\)，函数\(y = f(u)\)在点\(u_0\)处连续，则复合函数\(y = f(g(x))\)在\(x_0\)处连续，即\(\lim_{x \rightarrow x_0}f(g(x)) = f(g(x_0))\)

闭区间连续函数的性质

定理1.3

有界性定理
闭区间连续函数必有界

定理1.4

最大值(absolute maximum)和最小值(absolute minimum)，以及最值(absolute extrema)定理
闭区间连续函数一定可以取得最小或最大值

定理1.5

介值定理，the intermediate value theorem
设函数\(f(x)\)在闭区间\([a, b]\)上连续，且\(f(a) \not= f(b)\)，若\(\eta\)为介于\(f(a)\)与\(f(b)\)之间的任意实数，则至少存在一点\(x_0 \in [a, b]\)，使得\(f(x_0) = \eta\)

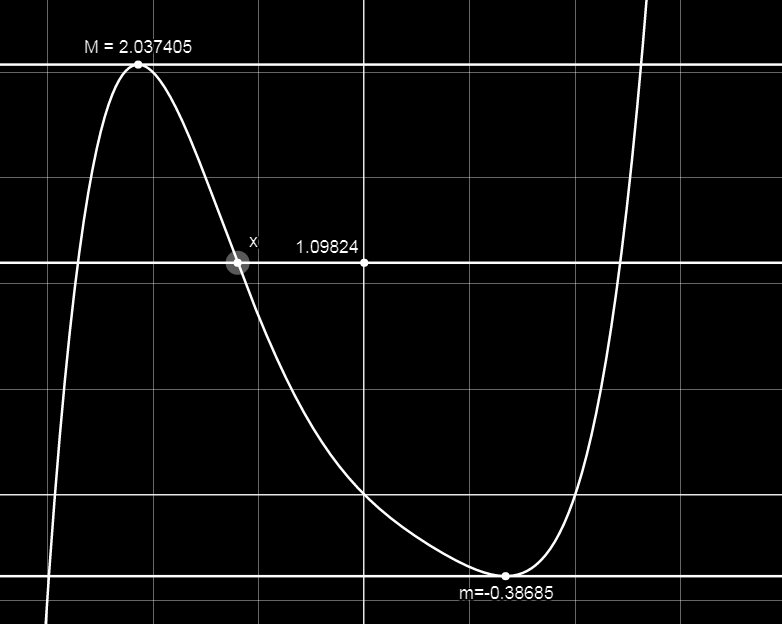
如图所示

定理1.5

零点定理
如果闭区间\([a, b]\)两端函数值异号(\(f(a) \cdot f(b) < 0\))，则函数\(f(x)\)一定存在一点\(\eta\)，使得\(f(\eta) = 0\)

导数与微分

定义2.1(导数的定义)

设函数\(y = f(x)\)在点\(x_0\)的某领域内有定义，自变量\(x\)在\(x_0\)处取得增量(Increment)\(\Delta x\)(\(x_0 + \Delta x\)仍在领域内)，函数值取得增量\(\Delta y = f(x_0 + \Delta x) - f(x_0)\)。若极限\(\lim_{\Delta x \rarr 0}\frac{\Delta y}{\Delta x}\)存在，则称函数\(f(x)\)在点\(x_0\)处可导(Differentiable)