2021ICPC济南E题

E、insideman

题意：

在一个圆上面有n个点，按顺时针依次编号为1....n，给定m条线连接（a，b），当两条线有交点并且交点在圆内的时候，将产生权值为（ai+bi）*（aj+bj）的奖励，但是其中有两个点没有用（所有与这两个点连接的线将不产生奖励），求最大可能的权值总和是多少。（n<=1e3,m<=1e5)

题解：

暴力求所有的交点是m^2。

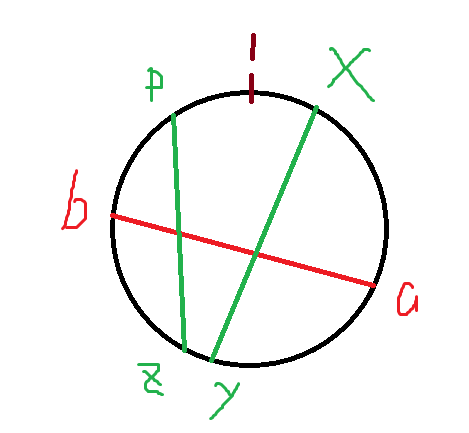
对上图，可知对（a,b）这条线，能够产生交点的肯定是(x,y)当且经当（1<=x<a,&&a<y<b)，或者（z,p)，当且仅当（a<z<b&&b<p<=n)。对于每一条线，将较小的节点叫主节点，较大的叫副节点。

 

 

 

 

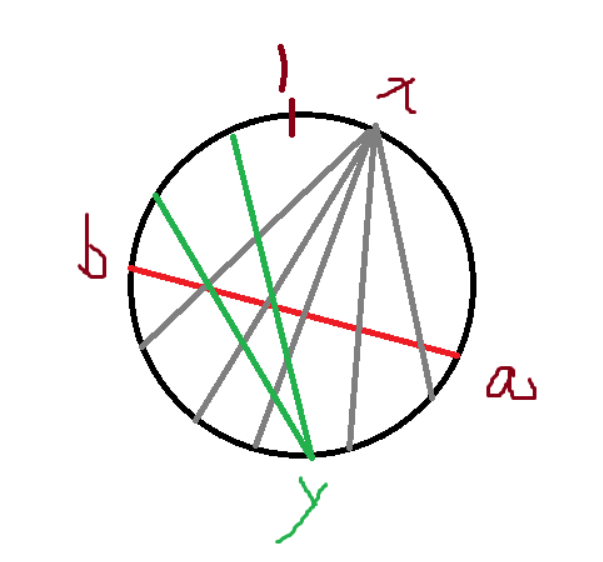
考虑前缀和优化计算次数sum[i] [j] 表示从1到j的以i为主节点的所有的线段的和,vis[i] [j]记录 i和 j是否存在相连的边

于是：sum[i] [j]=sum[i] [j-1] + (i+j)*vis[i] [j]

接着我们计算主节点比a小的，例如x在ab上产生的权值，显然就是(a+b)*(sum[x] [b-1]-sum[x] [a]),由于在1到a上有a-1个主节点，所以要进行a次计算。

对于主节点在ab之间的,例如y，就是(a+b)*(sum[y] [n]-sum[y] [b])。

对于主节点比b大的显然无法产生交点。

对每一条边，我们都从按照主节点从[1,a-1]和[a+1,b-1]算出在ab上产生的权值，对其求和即可得到ab和其它所有线段产生的权值之和。由于对于一个交点（假设为ab和cd的交点），我们不仅计算了ab在cd上产生的权值，还计算了cd在ab上产生的权值，所以计算的和除以2就是总的权值。

现在考虑找最大的值。要得到最大的可能的权值，我们只需要找到影响最小的组合即可。

假设ans[i]存的是i节点产生的权值，那么 i 和 j 的影响就是ans[i]+ans[j]-mp[i] [j] , 其中mp表示i和j共同的影响值

ans[i]显然我们可以在求总和的时候求，只要算与i有关的边那么ans [ i ]就加上这个边产生的权值即可。

那么，a，b的共同影响部分（mp[a] [b]）是不是就是边ab产生的权值呢？显然不是，比如ac与bd的交点，并不是边ab的权值，但是却与ab共同相关。

考虑用主节点来求解这个问题，还是在求总和的时候，如下图

对于边（a，b)每次我们遍历主节点的时候用temp[x] [a]和temp[x] [b]来记录x与a和x与b的共同影响，考虑到xu对ab的影响同时ab又对xu和xv产生的影响所以最终temp[x] [y]记录的是双倍的影响，对于y这种情况同理即可

 

 

 

 

 

 

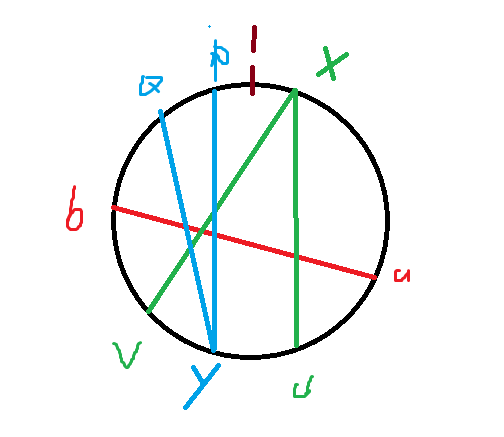
但是我们观察到u，v这种较大的节点并没有记录到，我门考虑反建立一个从大到小的遍历，将较大的作为主节点，然后从n到a遍历即可，这次只需要算出(假设u>b)temp[a] [u]和temp[b] [u]，不需要计算ans、总和。

 

 

 

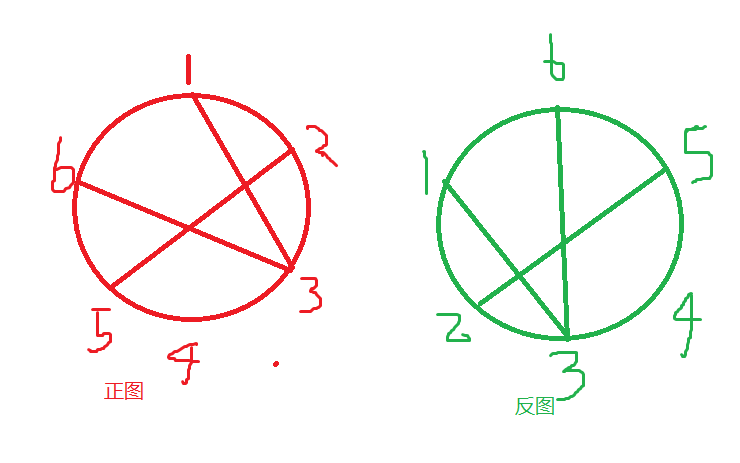
最后mp[i] [j] =temp[i] [j] /2 + 边（i，j）产生的权值。

code

#include <bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f3f3f
using namespace std;
const int N = 1e3 + 5;
int all = 0;

struct edge
{
	int x;
	int y;
}e[N * N];

int temp[N][N];		//暂存权值
int ans[N];		//i点的影响值
int mp[N][N];	//共同影响值
bool vis[N][N];	//i，j之间是否存在边
int sum[N][N];	//记录主节点为 较小 的值的sum
int psum[N][N];	//记录主节点为 较大 的值的sum

signed main()
{
	int n, m;
	scanf("%lld%lld", &n, &m);
	int a, b;
	for (int i = 1; i <= m; i++)
	{
		scanf("%lld%lld", &a, &b);
		if (a > b)swap(a, b);	//有序化
		if (a == b || a + 1 == b)continue;	//去掉不可能产生权值的边
		e[i] = { a,b };
		vis[b][a] = vis[a][b] = 1;
	}

	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			sum[i][j] = sum[i][j - 1] + (i + j) * (vis[i][j]);

	for (int i = n; i >= 1; i--)
		for (int j = n; j >= 1; j--)
			psum[i][j] = psum[i][j + 1] + (i + j) * vis[i][j];

	all = 0;
	for (int i = 1; i <= m; i++)
	{
		a = e[i].x;
		b = e[i].y;
		if (a == b)continue;
		for (int j = 1; j < a; j++)	//计算x的情况
		{
			int w = (a + b) * (sum[j][b - 1] - sum[j][a]);
			all += w;
			ans[a] += w;
			ans[b] += w;
			mp[a][b] += w;
			temp[j][a] += w;
			temp[j][b] += w;
		}
		for (int j = a + 1; j < b; j++)	//计算y情况
		{
			int w = (a + b) * (sum[j][n] - sum[j][b]);
			all += w;
			ans[a] += w;
			ans[b] += w;
			mp[a][b] += w;
			temp[j][b] += w;
			temp[a][j] += w;
		}

		b = e[i].x;
		a = e[i].y;
		if (a == b)continue;
		for (int j = n; j > a; j--)	//反建立的图的x情况
		{
			int w = (a + b) * (psum[j][b + 1] - psum[j][a]);
			temp[a][j] += w;
			temp[b][j] += w;
		}
		for (int j = a - 1; j > b; j--)	//反图的y情况
		{
			int w = (a + b) * (psum[j][1] - psum[j][b]);
			temp[j][a] += w;
			temp[b][j] += w;
		}
	}
	all >>= 1;
	int te = INF;

    //找最小的影响
	for (int i = 1; i < n; i++)
	{
		for (int j = i + 1; j <= n; j++)
		{
			te = min(te, ans[i] + ans[j] - mp[i][j] - (temp[i][j] >> 1));
		}
	}
	if (te == INF)te = 0;
	cout << all - te << endl;
}

　写在最后：对于重复的计算如果有更好的方法可以教教作者，毕竟我只是个刚入门的菜鸟。