CF1919E Counting Prefixes 题解

题目链接：https://codeforces.com/problemset/problem/1919/E

题意

输入一个单调非减序列 \(p\)，求问有多少个序列 \(a\)，使得：

• \(|a_i| = 1\)；

• 令 \(s_i = \sum_{j = 1}^i a_j\)，则 \(s\) 排序后与 \(p\) 相同。

序列长度不超过 \(5000\)。

题解

这题在赛时想错了很多地方，结果赛后调了很长很长时间，竟然得到正解了……

“排序后相同”这个条件等价于每个数的出现次数相同，也就是只要记录每个数的出现次数。为了方便分析，加入 \(p_0 = 0\)。

unordered_map<int, int> cnt;
cnt[0]++;
for (int i = 0; i < n; i++) cin >> p[i], cnt[p[i]]++;

首先显然 \(p\) 的值域是一段包含 \(0\) 的连续区间 \([-a, b]\)，可以一开始做完这个检查。

for (auto [k, v] : cnt) {
    if (k < 0) {
        if (!cnt.contains(k + 1)) {
            cout << 0 << "\n";
            return;
        }
    } else if (k > 0) {
        if (!cnt.contains(k - 1)) {
            cout << 0 << "\n";
            return;
        }
    }
}

\(a_i\) 为正负一，就代表 \(s\) 相邻两项是相邻数。观察 \(s\) 的可能形态，例如 \([0, 1, 2, 1, 2, 1, 0, -1, -2, -1, 0, 1, 2, 1]\)。

用 x 轴切开这个序列，则：

• \(s\) 被分为几段，其中除最后一段外开头和结尾均为 \(0\)，而最后一段只需要以 \(0\) 开始。我们把前一种叫做“闭区间”，后一种叫做“开区间”。（注意，当结尾为 \(0\) 时，没有最后一段开区间）

• 每一段内部要么全部大于 \(0\)，要么全部小于 \(0\)。

我们枚举开区间和闭区间各有多少段大于 \(0\)，有多少段小于 \(0\)，则可以按照“每一段内部都必须大于 \(0\)”计算，最终使用组合数合并答案即可。

Z ans = 0;
{
    int closed_cnt = cnt[0] - 1;
    for (int i = 0; i <= closed_cnt; i++) {
        for (int c = 0; c <= 1; c++) {
            ans += comb.get(closed_cnt, i) * calc(1, i, c) *
                    calc(-1, closed_cnt - i, 1 - c);
        }
    }
}

对 calc 这个子问题，考虑如何继续计算。使用一个扫描线从下往上扫描，则又有如下结论：

• 一个闭区间如果填入 \(x\) 个数，则会变为 \(x - 1\) 个闭区间。（也就是只填入一个数时，开区间在上一层消失；且至少要填入一个数）

• 一个开区间如果填入 \(x\) 个数，则会变为 \(x - 1\) 个闭区间和一个开区间。另外，如果填入 \(0\) 个数，这个开区间消失。

例如例子 \([0, 1, 2, 3, 2, 3, 2, 1, 0, 1, 2, 1]\)：

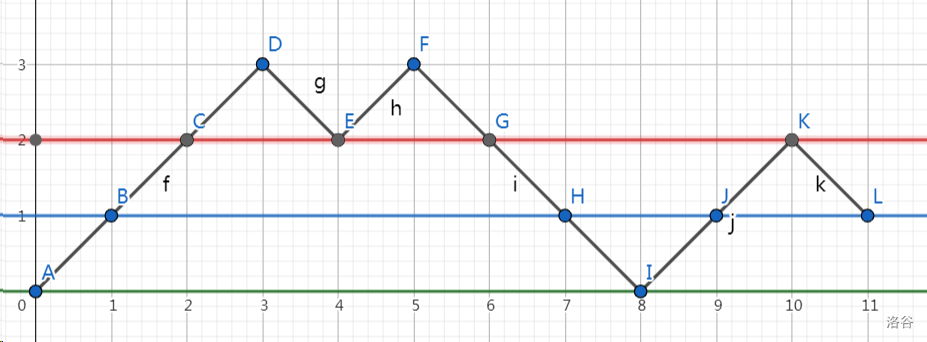
由于有两个 \(0\)，一开始有一个开区间和一个闭区间。

• 从 \(y = 0\) 向 \(y = 1\) 扫描，第一个闭区间内有两个数，仍为一个闭区间；最后一个开区间内也有两个数，变为一个闭区间和一个开区间。

• 从 \(y = 1\) 向 \(y = 2\) 扫描，第一个闭区间内有三个数，变为两个闭区间；第二个闭区间内有一个数，消失；最后一个开区间内没有数，消失。

• 从 \(y = 2\) 向 \(y = 3\) 扫描，两个闭区间内均只有一个数，均消失。

• 此时已经不存在任何区间，也不存在任何未使用的数，故这是一种可行的方案。

将状态记作 \((i, closed, open)\)，我们已经知道了状态的转移，考虑如何计数。记 \(i\) 的出现次数为 \(x\)，则：

• 若 \(open = 0\)，也就是所有的数都要填到闭区间中。每个闭区间至少要填入一个数，使用插板法知有 \(\binom{x - 1}{open - 1}\) 种方案。由于每个闭区间都使产生的新闭区间会减少一个，转移至的状态一定为 \((i + 1, x - closed, 0)\)，即 $calc(i, closed, 0) = \binom{x - 1}{open - 1} \cdot calc(i + 1, x - closed, 0) $。

• 否则，\(open = 1\)。若这个区间内不填数，则相当于 \(open = 0\) 的情况。否则，这个开区间被当做闭区间使用，相当于多出了一个闭区间的 \(open = 0\) 的情况，唯一的区别是下一层 \(open\) 也要为 \(1\)。

• 边界情况下 \(x = 0\)，此时只有 \(open = 0\) 且 \(closed \le 1\)，才是合法方案。

（这个思路其实是一种连续段 DP。）可以使用记忆化搜索实现。

unordered_map<i64, Z> cache;
function<Z(int, int, int)> calc = [&](int i, int closed_cnt, int open_cnt) {
    if (closed_cnt < 0) return Z(0);
    if (cnt[i] == 0) { return Z(closed_cnt == 0 && open_cnt <= 1); }
    i64 key = (i64)i * n * 2 + closed_cnt * 2 + open_cnt;
    if (cache.contains(key)) { return cache[key]; }
    Z res = 0;
    auto f = [&](int x, int closed_cnt, int open_cnt) -> Z {
        return comb.get(x - 1, closed_cnt - 1) *
                calc((i < 0) ? i - 1 : i + 1, x - closed_cnt, open_cnt);
    };
    int x = cnt[i];
    if (open_cnt) {
        res += f(x, closed_cnt + 1, 1);
        res += f(x, closed_cnt, 0);
    } else {
        res += f(x, closed_cnt, 0);
    }
    return cache[key] = res;
};

但需要注意，我们这样的计算中包含了“开区间一个数都没有”的情况，这样的情况下，开区间会被分为正负各计算一次，因此需要减去这样的重复情况修正。修正后统计答案的代码如下：

Z ans = 0;
{
    int closed_cnt = cnt[0] - 1;
    for (int i = 0; i <= closed_cnt; i++) {
        for (int c = 0; c <= 1; c++) {
            ans += comb.get(closed_cnt, i) * calc(1, i, c) *
                    calc(-1, closed_cnt - i, 1 - c);
        }
        ans -= comb.get(closed_cnt, i) * calc(1, i, 0) *
                calc(-1, closed_cnt - i, 0);
    }
}
cout << ans << "\n";

复杂度分析

状态数是 \(O(n^2)\) 的，因此时空复杂度均为 \(O(n^2)\)。但我的提交的时空表现都很好。

如果仔细分析，实际上这个做法可以做到线性时间复杂度。关键在于 DP 的每一层中，合法的值最多只有两个第二维下标，因此我们从最上层和最下层开始，向中间递推，实时维护不为 \(0\) 的所有值即可，这部分甚至可以做到 \(O(1)\) 空间复杂度（注意组合数的 \(O(n)\) 空间不可避免）。

为什么这个结论成立？考虑从状态 \((1, t, 1)\) 出发，会走到的所有状态。首先考虑向 \(open = 1\) 转移的分支：

\[\begin{aligned} (1, t, 1) &\to (2, x_1 - t - 1, 1) \\ &\to (3, x_2 - (x_1 - t -1) -1 = x_2 - (x_1 - t), 1) \\ &\to (4, x_3 - (x_ 2 - (x_1 - t)) - 1, 1) \\ &\to (5, x_4 - (x_3 - (x_ 2 - (x_1 - t))), 1) \\ &\to \cdots \end{aligned} \]

可以看到，第二维下标有 \(\sum_{i =0} ^{n} (-1)^i x_{n-i} - [n \equiv 0 \mathbin{mod} 2]\) 的形式。而另一条向 \(open=0\) 分支是“一条路走到黑”，根据奇偶分类讨论，不难得到每层至多只有两个相差 \(1\) 的第二维下标。

从结束点 \((mx+1, 0/1)\) 倒过来分析，也可以更方便地得到类似的结论。

但注意，我们记忆化搜索的代码由于并不知道当前在的状态是否合法，因此还是最坏 \(O(n^2)\) 的。

而一份使用递推真正做到线性时间、常数空间的代码如下：

using Z = atcoder::modint998244353;
using C = modint::comb<Z>;
C comb{5000 + 7};
using T = array<array<Z, 2>, 2>;

void solve() {
    int n;
    cin >> n;
    vector<int> p(n), cnt(2 * n + 1);
    cnt[n]++;
    for (int i = 0; i < n; i++) { cin >> p[i], cnt[p[i] + n]++; }
    int mn = p[0], mx = p[n - 1];
    T ans1, ansn1;
    int base1 = 0, basen1 = 0;
    auto trans = [](int &base, T &lst, int c) {
        T now;
        base = c - base;
        now[0][0] = comb.get(c - 1, base - 1) * lst[0][0];
        now[0][1] = comb.get(c - 1, base - 1) * lst[0][0] +
                    comb.get(c - 1, base) * lst[1][1];
        now[1][1] = comb.get(c - 1, base - 1) * lst[0][1];
        lst = std::move(now);
    };
    ans1[0] = {1, 1};
    for (int i = mx; i >= 1; i--) trans(base1, ans1, cnt[i + n]);
    ansn1[0] = {1, 1};
    for (int i = mn; i <= -1; i++) trans(basen1, ansn1, cnt[i + n]);
    Z ans = 0;
    int closed_cnt = cnt[n] - 1;
    for (int b0 : {0, 1}) {
        for (int b1 : {0, 1}) {
            if (base1 + basen1 - b0 - b1 == closed_cnt) {
                int i = base1 - b0;
                ans += comb.get(closed_cnt, i) * ans1[b0][0] * ansn1[b1][1];
                ans += comb.get(closed_cnt, i) * ans1[b0][1] * ansn1[b1][0];
                ans -= comb.get(closed_cnt, i) * ans1[b0][0] * ansn1[b1][0];
            }
        }
    }
    cout << ans.val() << "\n";
}

请检查 CF 上提交。

拓展

ARC146E 题与这题基本一样，区别是：

• 出现不同数的个数、出现次数均在 \(2 \times 10^5\) 级别；

• 出现次数以数组的形式给出（不限制总和），且均大于 \(0\)；

• 不限制 \(s\) 的开头为 \(0\)，且出现的所有数大于 \(0\)。

事实上，我们可以以基本相同的方式解决该问题，不同点如下：

• 首先可以只考虑上半平面，不需要对两部分分别计算再合并答案。

• 由于出现次数均大于 \(0\)，可以从 \(1\) 往上扫。

• 由于不限制开头第一个数，左右两边都可以有一个开区间。也就是说需要考虑 \(open = 2\) 时的转移。转移应该容易类推得出。

• 不限制出现次数的总和，可以按照 \(closed <= \max(cnt)\) 剪枝。

与上面不同，我们只进行了一次搜索，故可以确保时空复杂度均为线性。

观察这题的官方题解，复杂度分析可能会更清晰，更容易理解。

参考代码：

using Z = atcoder::modint998244353;
using C = modint::comb<Z>;

constexpr int M = 200000 + 233;
C comb{M};

void solve() {
    int n;
    cin >> n;
    vector<int> cnt(n + 3, 0);
    for (int i = 1; i <= n; i++) cin >> cnt[i];
    unordered_map<i64, Z> cache;
    function<Z(int, int, int)> calc = [&](int i, int closed_cnt, int open_cnt) {
        if (closed_cnt < 0 || closed_cnt > M) return Z(0);
        if (cnt[i] == 0) { return Z(closed_cnt == 0); }
        i64 key = (i64)i * M * 3 + closed_cnt * 3 + open_cnt;
        if (cache.contains(key)) { return cache[key]; }
        Z res = 0;
        auto f = [&](int x, int closed_cnt, int open_cnt) -> Z {
            return comb.get(x - 1, closed_cnt - 1) *
                   calc(i + 1, x - closed_cnt, open_cnt);
        };
        int x = cnt[i];
        if (open_cnt == 2) {
            res += f(x, closed_cnt + 2, 2);
            res += 2 * f(x, closed_cnt + 1, 1);
            res += f(x, closed_cnt, 0);
        } else if (open_cnt == 1) {
            res += f(x, closed_cnt + 1, 1);
            res += f(x, closed_cnt, 0);
        } else {
            res += f(x, closed_cnt, 0);
        }
        return cache[key] = res;
    };
    int closed_cnt = cnt[1] - 1;
    cout << calc(2, closed_cnt, 2).val() << "\n";
}