Codeforces Round 921 (Div. 1) 记录（A-D）

比赛链接：https://codeforces.com/contest/1924

官解链接：https://codeforces.com/blog/entry/125137

这场整体来说表现还可以，最终 performance \(2431\)，delta \(+33\)。但回过头来复盘离自己的期望还差很多，离 red 任重而道远。上次打（非 1+2） Div. 1 比赛还是在去年九月，也可能有手生了的影响。

CF1924A. Did We Get Everything Covered?

不错的贪心题。进入状态慢了，写了几个小错误调到 \(12\) min 才通过，好在 \(0\) dirt。

题意

给定字符集大小 \(|\Sigma | = k \le 26\)，和长度为 \(m\) 的字符串 \(s\)。给定 \(n\)，问是否所有 \(t \in {\Sigma}^n\) 都是 \(s\) 的子序列。若不是，给出一个不满足条件的 \(t\)。

解法

关键结论：\(s\) 对 \(n\) 满足条件，当且仅当可以分割 \(s = s_1 + s_2\)，其中 \(s_1\) 对 \(n - 1\) 满足条件，而 \(s_2\) 中 \(\Sigma\) 中字母各至少出现一次（可以考虑如何证明）。于是可以从左向右扫描，维护当前满足条件的长度，并在每次访问完整个字符集时更新。判断长度是否小于 \(n\) 即可。

答案为 NO 时，不符合条件的串的构造需要小心。给出一个显然正确的构造：每次更新长度时，记录最后一次遇到的字母，添加到答案末尾。之后向结尾不断增加（当前段）未出现的字母直至长度为 \(n\)。使用状态压缩技术，时间复杂度 \(O(n + m)\)。

代码实现

void solve() {
    int n, k, m;
    cin >> n >> k >> m;
    string s;
    cin >> s;
    int l = 0, vis = 0;
    string ans;
    for (char c : s) {
        vis |= 1 << (c - 'a');
        if (vis == (1 << k) - 1) {
            ans += c;
            l++, vis = 0;
        }
    }
    if (l >= n) {
        cout << "YES\n";
    } else {
        cout << "NO\n";
        int b = countr_one((unsigned)vis);
        while ((int)ans.size() < n) ans += char('a' + b);
        cout << ans << "\n";
    }

CF1924B. Space Harbour

一开始想写线段树，结果答案错了还发现自己不会写了……遂更换做法，然后又被珂朵莉树细节坑了，浪费很多时间还 dirt \(+2\)。下次写线段树还是用 ACL 吧。

题意

有 \(n \le 3 \times 10^5\) 个点 \([1, n]\)，其中 \(m\) 个点有太空港，每个太空港有权值 \(v\)。

每个点的代价为其左侧最近太空港的权值乘以它到右侧最近太空港的距离。特别地，若一个点已经有太空港，代价为 \(0\)。要求支持 \(q \le 3 \times 10^5\) 次两种查询：

• 在某个（之前没有太空港的）点增加一个太空港。

• 查询区间 \([l, r]\) 中点的代价总和。

题解

考虑两个相邻的位置为 \(x\)，\(y\) 的太空港之间的代价：区间 \([x + 1, y]\) 的代价形成一个等差数列，从右向左看首项为 \(0\)，公差为 \(v_x\)。

实时维护这些线段（可以使用 set），而对于代价和的区间查询，直接使用区间加等差数列（一次函数）的线段树完成，就可以快速完成这题（这也是 jiangly 的做法）。当然区间加等差数列、区间求和应该也可以纯树状数组完成维护，但我不会写，也不建议这么写。

然而不巧的是，我在写线段树时发现自己忘记怎么手写这样的线段树了，而又没有临时切换到 ACL 等模板。于是我切换到了一种类似分块的方法：对完全包括的线段，使用树状数组直接求和。而两端的可能不完全包含的线段，拿出来使用等差数列求和公式单独处理即可。另外注意两端可能在同一个线段内。

两种解法的时间复杂度都是 \(O((n + q) \log n)\)。

参考代码

线段树（偷了 jiangly 的板子）：提交

树状数组：提交

CF1924C. Fractal Origami

很简单的题，手动折一下基本有思路了，再加点高中数学实现。\(< 20\) min 完成。

题意

有一张边长为 \(1\) 的纸。递归地将四个角向内折叠 \(n \le 10^9\) 次。最后将整张纸展开。求峰和谷长度的比值 \(\dfrac M V\)。若将它表示为 \(A + B \sqrt2\)（\(A\)，\(B\) 是有理数），给出 \(B\) 的有理数取模形式。

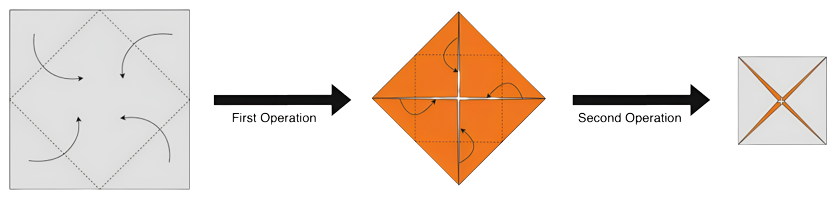
题解

只要分别算出 \(M\) 和 \(V\) 的值，之后求出比值，并化为题目需要的形式即可。

考虑每次折叠对 \(M\) 和 \(V\) 的影响。第一次折叠是特殊的，它会单独将 \(V\) 增大 \(2 \sqrt2\)。而对于之后第 \(i \ge 2\) 次折叠：

• 折叠后正方形的边长为 \((\sqrt2)^{-i}\)。

• 展开一次，我们可以看到四个谷，它们的总长度是（折叠后）边长的四倍。

• 我们还要再展开 \(i - 1\) 次。由对称性，每次展开后原来的峰或谷都会变成相同长度的峰和谷，即总长度变为原来的两倍。它们的总长度是 \(4 (\sqrt2)^{-i} \cdot 2^{i-1} = 2 (\sqrt2)^{i}\)，峰和谷各占一半。

• 因此我们可以下结论，第 \(i\) 次折叠新生成的峰和谷的长度均为 \((\sqrt2)^{i}\)。

因此 \(M = \sum\limits_{i = 2}^n (\sqrt2)^{i}, V = 2\sqrt2 + M\)。使用等比数列求和公式可以逐步计算答案，时间复杂度 \(O(\log n)\)。

代码实现

void solve() {
    int n; cin >> n;
    Z ma = 0, mb = 0, va = 0, vb = 2;
    n--;
    int na = (n + 1) / 2, nb = n / 2;
    Z a = 2 * (Z(2).pow(na) - 1), b = 2 * (Z(2).pow(nb) - 1);
    ma += a, va += a;
    mb += b, vb += b;
    Z ans = (ma * vb - mb * va) / (2 * vb * vb - va * va);
    cout << ans << "\n";
}

CF1924D. Balanced Subsequences

虽然 C 很简单也出的很快，但只剩二十多分钟，所以直接就没有仔细看 D。

题意

求有 \(n\) 个左括号，\(m\) 个右括号，且最长匹配子序列长度为 \(2k\)（即最长匹配子序列有 \(k\) 对括号）的括号串数量。

题解

记 \(f(n, m, k)\) 为“最长匹配子序列至多有 \(k\) 对”的数量，则要求的就是 \(f(n, m, k) - f(n, m, k - 1)\)。若 \(k >= \min(n, m)\)，则所有序列均满足条件，答案即为 \(\binom{n + m}{m}\)，故下面假设 \(k < \min(n, m)\)。\(k = 0\) 是平凡的（只有右括号+左括号一种序列），因此再假设 \(k > 1\)。

首先翻译一下官解。

• 开头为右括号的串显然数量为 \(f(n, m-1, k)\)；
• 开头为左括号的串数量为 \(f(n-1, m, k-1)\)，即“原串最长匹配对数为 \(k\)”与“删去最左侧左括号后最长匹配对数为 \(k-1\)”等价。这部分不是那么显然，考虑一种求最长匹配子序列的贪心方法：每当遇到右括号，就将其与最近未匹配的左括号匹配。由于 \(k < \min(n, m)\)，最终留下未匹配的子序列一定是一些右括号紧跟一些左括号。则第一个左括号一定被匹配，且删去它，剩余串的匹配对数一定减去 \(1\)。反证：否则（若不减），（由于右括号的数量不变）一定仍存在未匹配的右括号，重新加回最左侧的左括号会导致匹配对数增加。

则有递归式 \(f(n, m, k) = f(n, m-1, k) + f(n-1, m, k-1)\)。结合边界条件 \(f(n, m, 0) = 1 = \binom{n+m}{0}\) 以及 \(f(n, m, \min(n, m)) = \binom{n+m}{m} = \binom{n+m}{ \min(n, m)}\)，使用奇妙的数学归纳法即可得到 \(f(n, m, k) = \binom{n + m}{k}\)。

但这个数学归纳的过程并不是很直观。下面介绍更容易理解的折线法，这个做法是折线法求卡塔兰数的推广。

考虑在 \(n \times m\) 的网格图上，从 \((0, 0)\) 点移动到 \((n, m)\)，左括号对应向右移动一步，右括号对应向上移动一步。那么未被匹配的右括号的数量就是 \(x - y\) 的最大值。要让匹配括号对数不超过 \(k\)，\(x - y\) 的最大值要不小于 \(m - k\)，即折线与直线 \(x - y = m - k\) 相交。

我们在第一个交点处，将之后的折线关于直线翻转，则终点变为 \((n + m - k, k)\)。且终点为 \((n + m - k, k)\) 的折线和满足前面条件的折线之间是双射关系（因为终点为 \((n + m - k, k)\) 的折线一定穿过直线 \(x - y = m - k\)，而翻转操作又是可逆的）。则方案数即为 \(\binom{n + m - k + k}{k} = \binom{n + m}{k}\)。

代码实现

Z get(int n, int m, int k) {
    if (k >= min(n, m)) return comb.get(n + m, m);
    else return comb.get(n + m, k);
}

void solve() {
    int n, m, k;
    cin >> n >> m >> k;
    cout << get(n, m, k) - get(n, m, k - 1) << "\n";
}