超几何分布：概念、期望、方差

N个样本中，有M个次品，不放回的抽出n个，其中的次品数X，服从超几何分布，记作X~H(n, M, N)。

随机变量X的概率分布：

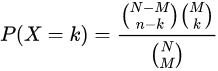
 随机变量X的期望：

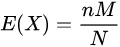
 随机变量X的方差：

 

---

 

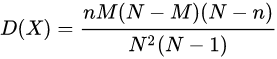
有13件合格品，2件次品，不放回的抽出3个，记其中次品数X，求随机变量X的分布列、期望、方差。

N=15，M=2，n=3，X~H(3, 2, 15)。其中，X取值可以是0，1，2。

P(X=0)=22/35

P(X=1)=12/35

P(X=2)=1/35

E(X)=nM/N=3*2/15=2/5

E(X)=0×22/35+1×12/35+2×1/35=14/35=2/5

D(X)=3*2*(15-2)*(15-2)/15^2/(15-14)=156/525=52/175

E(X^2)=0^2×22/35+1^2×12/35+2^2×1/35=16/35

E(X)^2=(2/5)^2=4/25

D(X)=E(X^2)-E(X)^2=16/35-4/25=52/175。

以四格表形式表示

情况	选中	未选中	合计
次品	X	M-X	M
合格品	n-X	N-n-M+X	N-M
合计	n	N-n	N

一般四格表

分组	分类1	分类2	合计
A组	a	b	a+b
B组	c	d	c+d
合计	a+c	b+d	N

未完