NOIP2025模拟6 & 2025多校冲刺NOIP模拟赛1

T1：汉谟拉比(crazy)

思路：

我们知道期望是概率的加和，而概率最后要除以 n ，可题目要求最后的答案再乘 n 。综合起来，即我们要求的是最少的被咬的次数。

然后考虑\(DP。\)

先说暴力 \(O(nm^2)\) 的。

设 \(dp_{i,j}\) 表示前 \(i\) 个数和为 \(j\) 最少被咬的次数。

我们预处理出 \(s_i=\sum _{j=1} ^ n [ ~ a_j<i ~ ]\)，然后的状态转移就好想了。

\[dp_{i,j}=min\{dp_{i,k}+s_{j-k}\} \]

最后有一个小剪枝，\(k\) 一定不会大于 \(min(j,\frac{m}{i})\)

代码：

$code$

#include<iostream>
#include<cstring>
using namespace std;
const int N=1005,M=5005;
int n,m,a[N],s[M],dp[M],f[M];
int main(){
	freopen("crazy.in","r",stdin);
	freopen("crazy.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		s[a[i]-1]++;
	}
	for(int i=M-1;i;i--) s[i-1]+=s[i];
	for(int i=1;i<=n;i++){
		int maxn=m/i;
		memset(dp,0x3f,sizeof(dp));
		for(int j=0;j<=m;j++){
			for(int k=0;k<=min(j,maxn);k++){
				dp[j]=min(dp[j],f[j-k]+s[k]);
			}
		}
		memcpy(f,dp,sizeof(dp));
	}
	cout<<dp[m]<<'\n';
	return 0;
}

T2：虫洞折跃(flip)

思路：

简单的 \(dp\) 。（赛时没发现性质以为是假的）

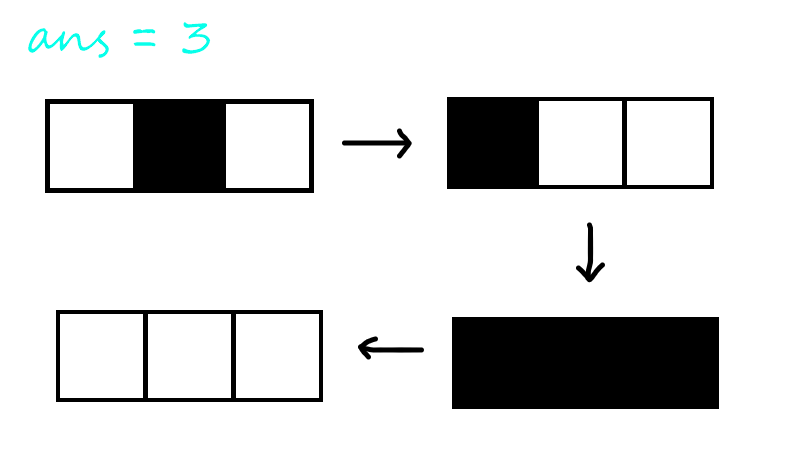
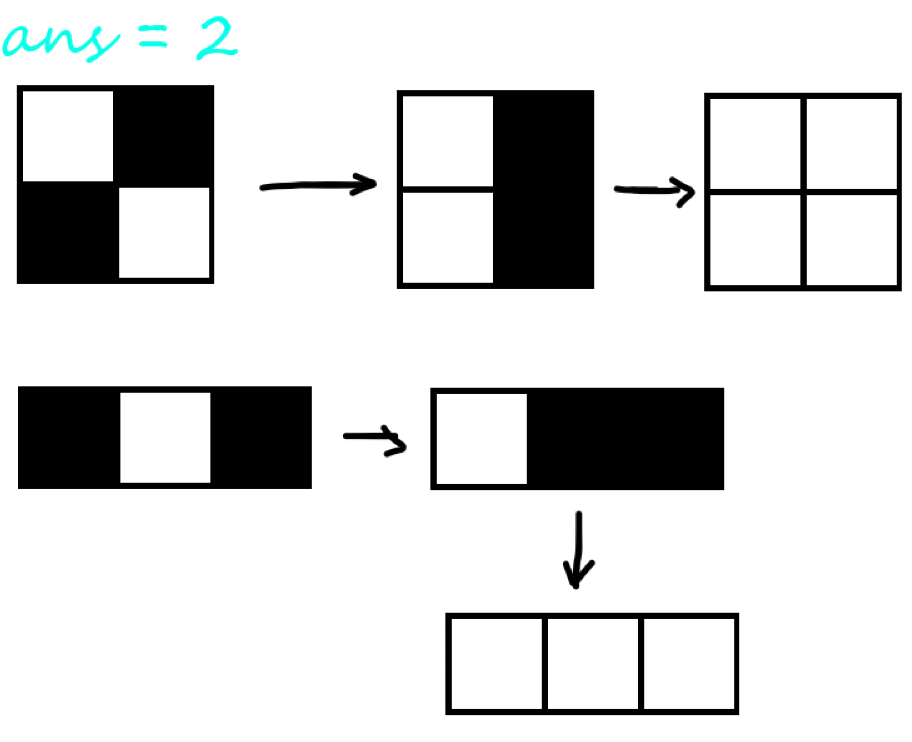
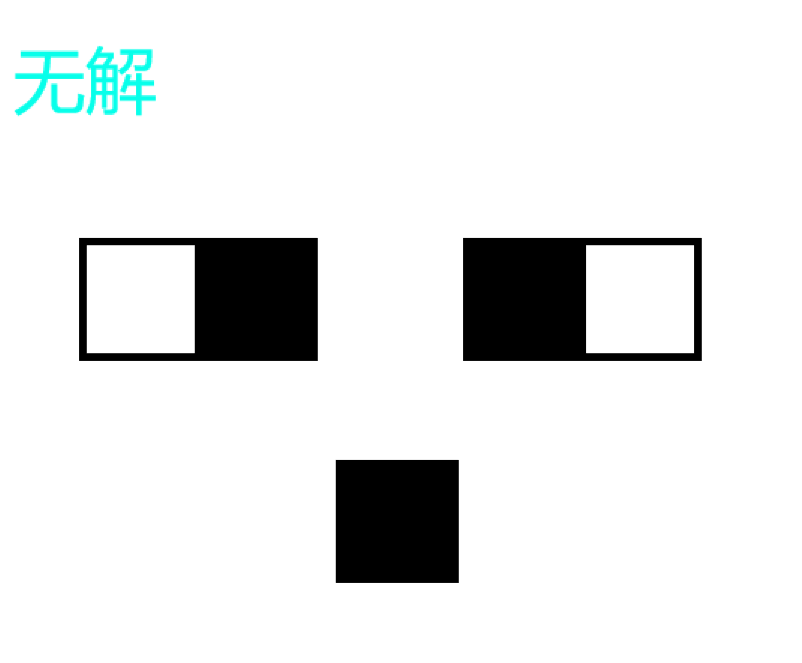
先说性质，我们从整张图中揪一部分出来

我们先随便摘出一条路径（不一定是最优的）：1100001111。

对于这条路径我们需要翻转两次。

同一翻转矩阵内不会使相同的变的不同，也不会使不同的变的相同。

所以我们只需要统计出有多少次字符不同的转折点，最后再除以2就好了。

需要注意的是，首尾应该是 \(0\)，若是 \(1\) 的话也要加 \(1\)。

考虑设 \(dp_{i,j}\) 表示到 \((i,j)\) 这个格子的最少的翻转点的数量。

显然 \((i,j)\) 这个点只能从 \((i-1,j)\) 和 \((i,j-1)\) 转移过来。

然后这道题就变成了一道特判题。

代码：

$code$

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
const int N=1e3+5;
int T,n,m,x,y,z,w,a[N][N],dp[N][N];
bool flag;
int main(){
	freopen("flip.in","r",stdin);
	freopen("flip.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>T;
	while(T--){
		flag=0;
		cin>>n>>m;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				cin>>a[i][j];
			}
		}	
		if(n==1){
			if(m==1){
				if(a[1][1]) cout<<"Impossible"<<'\n';
				else cout<<0<<'\n';
				continue;
			}else if(m==2){
				if(a[1][1]!=a[1][2]) cout<<"Impossible"<<'\n';
				else{
					if(x==1) cout<<1<<'\n';
					else cout<<0<<'\n';
				}
				continue;
			}else if(m==3){
				if(!a[1][1]&&a[1][2]&&!a[1][3]){
					flag=1;
					cout<<3<<'\n';
					continue;
				}
			}else{
				int f=0;
				for(int i=1;i<=m;i++){
					if(a[1][i]){
						f++;
					}
				}
				if(f==1){
					cout<<2<<'\n';
					continue;
				}
			}
		}
		if(n==2&&m==2){
			if(!a[1][1]&&a[1][2]&&a[2][1]&&!a[2][2]){
				cout<<2<<'\n';
				continue;
			}
		}
		memset(dp,0x3f,sizeof(dp));
		dp[1][1]=a[1][1];
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				if(i==1&&j==1) continue;
				dp[i][j]=min(dp[i][j],min(dp[i-1][j]+(a[i-1][j]!=a[i][j]),dp[i][j-1]+(a[i][j-1]!=a[i][j])));
			}
		}
		cout<<(dp[n][m]+1)/2<<'\n';
	}
	return 0;
}

T4：逃离冰场(skate)

真有人能在赛时瞪出它是最短路吗？

好吧，其实是有的。

手模一下，我们可以发现我们只有两种移动方式：

一种是移动到冰块的旁边，我们只需要 \(1\) 步；

一种是移动到相邻的在该方向上不挨着冰块的格子里，我们需要 \(2\) 步。

就像上述这样建边，然后跑最短路就行。

\(spfa\) 和 \(dij\) 都可以。

代码：

$code$

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e3+5;
int n,m,a[N][N],l1[N][N],l2[N][N],r1[N][N],r2[N][N],st,sx,sy,ex,ey,cnt,head[N*N],dis[N*N];
bool vis[N*N];
char ch;
struct flower{
	int to,nxt,val;
}e[N*N*8];
inline void add(int x,int y,int z){
	e[++cnt].to=y;
	e[cnt].val=z;
	e[cnt].nxt=head[x];
	head[x]=cnt;
}
inline void spfa(int s){
	memset(dis,0x3f,sizeof(dis));
	dis[s]=0;
	vis[s]=1;
	queue<int> q;
	q.push(s);
	while(!q.empty()){
		int x=q.front();q.pop();
		for(int i=head[x];i;i=e[i].nxt){
			int y=e[i].to;
			if(dis[y]>dis[x]+e[i].val){
				dis[y]=dis[x]+e[i].val;
				if(!vis[y]){
					q.push(y);
					vis[y]=1;
				}
			}
		}
		vis[x]=0;
	}
}
int main(){
	freopen("skate.in","r",stdin);
	freopen("skate.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>ch;
			a[i][j]=(ch=='#');
		}
	}
	cin>>sx>>sy>>ex>>ey;
	for(int i=1;i<=n;i++){
		st=0;
		for(int j=1;j<=m;j++){
			if(a[i][j]) st=j;
			else l1[i][j]=st;//左边的第一个冰块
		}
	}
	for(int i=1;i<=n;i++){
		st=m+1;
		for(int j=m;j;j--){
			if(a[i][j]) st=j;//右边的第一个冰块
			else r1[i][j]=st;
		}
	}
	for(int i=1;i<=m;i++){
		st=0;
		for(int j=1;j<=n;j++){
			if(a[j][i]) st=j;
			else l2[j][i]=st;//上面的第一个冰块
		}
	}
	for(int i=1;i<=m;i++){
		st=n+1;
		for(int j=n;j;j--){
			if(a[j][i]) st=j;
			else r2[j][i]=st;//下面的第一个冰块
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]) continue;
			if(j>l1[i][j]+1){
				add((i-1)*m+j,(i-1)*m+l1[i][j]+1,1);
				add((i-1)*m+j,(i-1)*m+j-1,2);
			}
			if(j<r1[i][j]-1){
				add((i-1)*m+j,(i-1)*m+r1[i][j]-1,1);
				add((i-1)*m+j,(i-1)*m+j+1,2);
			}
			if(i>l2[i][j]+1){
				add((i-1)*m+j,(l2[i][j])*m+j,1);
				add((i-1)*m+j,(i-2)*m+j,2);
			}
			if(i<r2[i][j]-1){
				add((i-1)*m+j,(r2[i][j]-2)*m+j,1);
				add((i-1)*m+j,i*m+j,2);
			}
		}
	}//建图
	spfa((sx-1)*m+sy);//最短路
	if(dis[(ex-1)*m+ey]>1e6) cout<<"-1"<<'\n';//无解
	else cout<<dis[(ex-1)*m+ey]<<'\n';//输出
	return 0;
}