CSP-S模拟17

\(T1：\) 小争（zheng）

前言： 赛时想了一个函数模型，但是当时好像少情况了。吃饭路上想到缺失的情况，但是发现貌似无解（也可能是码力太差），只能跟着改正解了。对了，洛谷的那个题，它的空间限制....有点一言难尽，反正我过不去。（补：可能解法不一样，洛谷的题应该是\(O(n^2)\)的）

思路：

通过题意我们不难发现，题目要我们求将一个序列转化为一个单峰需要删去多少元素。可以想到枚举每一个元素作为峰顶（最大值）然后求出以当前值为最大值的最长不下降序列和最长不上升序列的长度和加一就行。但是，显然此时的时间复杂度为\(O(n^2)\)，是不可接受的，于是我们考虑线段树优化掉求最长不上升/不下降子序列的那个\(n\)，此时时间复杂度就可以接受啦~~

请看VCR代码：

点击查看代码

#include<iostream>
#include<cstring>
#include<algorithm>
#define lid id<<1
#define rid id<<1|1
using namespace std;
const int N=17805;
int n,a[N],b[N],l1[N],l2[N],ans;
struct node{
	int max;
}tr[N<<2];
inline void insert(int id,int l,int r,int pos,int val){
	if(l==r){
		tr[id].max=val;
		return ;
	}
	int mid=(l+r)>>1;
	if(pos<=mid) insert(lid,l,mid,pos,val);
	else insert(rid,mid+1,r,pos,val);
	tr[id].max=max(tr[id].max,max(tr[lid].max,tr[rid].max));
}
inline int query(int id,int l,int r,int pos){
	if(pos>=r) return tr[id].max;
	int ans=0;
	int mid=(l+r)>>1;
	ans=max(ans,query(lid,l,mid,pos));
	if(pos>mid) ans=max(ans,query(rid,mid+1,r,pos));
	return ans;
}//线段树优化 
int main(){
//	freopen("zheng.in","r",stdin);
//	freopen("zheng.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
	int l=unique(b+1,b+1+n)-b-1;
	sort(b+1,b+1+l);
	for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+1+l,a[i])-b;//离散化 
	for(int i=1;i<=n;i++){//上升 
		l1[i]=query(1,1,n,a[i])+1;
		insert(1,1,n,a[i],l1[i]);
	}reverse(a+1,a+1+n);memset(tr,0,sizeof(tr));
	for(int i=1;i<=n;i++){//反过来求上升即为下降 
		l2[i]=query(1,1,n,a[i])+1;
		insert(1,1,n,a[i],l2[i]);
	}reverse(a+1,a+1+n);reverse(l2+1,l2+1+n);
	for(int i=1;i<=n;i++){
		ans=max(ans,l1[i]+l2[i]-1);
	}cout<<n-ans<<endl;
	return 0;
}

\(T2：\)尽梨了（de）（注：没找到原题面，\(but\)来源：loj3627 「2021 集训队互测」这是一道集训队胡策题）

题意：

有一个\(n~×~n\)的\(01\)矩阵\(c\)，她想知道有多少长度为\(n\)的\(01\)序列\(a\) , \(b\)，满足\(c_{i,j}=a_i\)或\(a_{i,j}=b_j\)，答案对\(998244353\)取模。

输入：
第一行一个整数\(n\)表示矩阵大小，接下来\(n\)行，每行一个长度为\(n\)的\(01\)字符串\(c_i\)，其中第\(j\)个字符表示\(c_{i,j}\)。

样例输入：

3
010
101
010

样例输出：

2

前言：

赛时其实没读懂题，而且 由于拼好赛的缘故（其实是我瞎） 没找到大样例，所以捏，根本就没写。（其实写了一个乱搞的东西，但是绝对与题意不符就是了）

思路：借鉴自大佬

先中译中一下题面， （毕竟我读了一个小时才读懂的题www） ，就是对于任意一个\(c_{i,j}\)都只有两种情况，要么它等于\(a_i\)，要么它等于\(b_j\)。问有多少组\(a\) , \(b\)符合题意。

我们设\(a\)中有\(x\)个\(1\)，\(b\)中有\(y\)个\(1\)，然后\(c_{i,j}\)中有\(sum1\)个等于\(a\)，\(sum2\)个等于\(b\)，我们不难得到等式\(sum1+sum2-x*y-(n-x)*(n-y)=n^2\)（解释一下：其实就是一个简单的容斥原理【我不知道对不对啊，反正我是这么理解的】具体见下图）

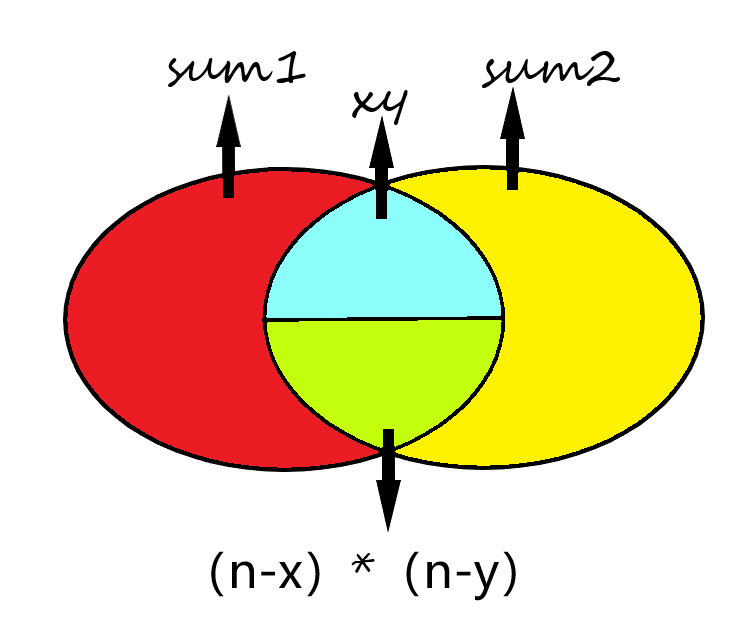
然后我们可以对\(1\)的放置进行贪心啦~~

\(ps：\)真的如题所说，尽梨了......

代码时间：

code time

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5010,mod=998244353;
char s[N];int a[N][N],c1[N],c2[N],h1[N],top1,h2[N],top2,s1[N],s2[N],n,sum1[N],sum2[N],sr1[N],sr2[N],ans,C[N][N],v1[N],v2[N];
bool cmp(int x,int y){return x>y;}
signed main(){
	scanf("%d",&n);
	for(int i=0;i<=N-10;i++) C[i][0]=1;
	for(int i=1;i<=N-10;i++) for(int j=1;j<=i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;//预处理组合数 
	for(int i=1;i<=n;i++){
		scanf("%s",s+1);//输入 
		for(int j=1;j<=n;j++) a[i][j]=s[j]-'0';//读入矩阵 
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			c1[i]+=(a[i][j]==1);//每行 
			c2[i]+=(a[j][i]==1);//每列 
		}
	}//统计每行每列的1的个数 
	memset(h1,-1,sizeof(h1));memset(h2,-1,sizeof(h2));//初始化 
	sort(c1+1,c1+n+1,cmp);sort(c2+1,c2+n+1,cmp);//排序 
	for(int i=1;i<=n;i++){
		if(c1[i]!=h1[top1]) h1[++top1]=c1[i],s1[top1]=1;
		else s1[top1]++;//每行的 
		if(c2[i]!=h2[top2]) h2[++top2]=c2[i],s2[top2]=1;
		else s2[top2]++;//每列的 
	}///统计每种情况及其出现的次数 
	for(int i=top1;i>=1;i--) sr1[i]=sr1[i+1]+(n-h1[i])*s1[i];//从当前情况行以后的0的个数 
	for(int i=top2;i>=1;i--) sr2[i]=sr2[i+1]+(n-h2[i])*s2[i];//从当前情况列以后的0的个数 
	for(int x=0;x<=n;x++){//枚举x 
		int rx=x;//剩余可填1的位置 
		v1[x]=1;//情况数 
		for(int i=1;i<=top1;i++){//从行内1多的位置开始填 
			if(rx>=s1[i]) sum1[x]+=s1[i]*h1[i],rx-=s1[i];//这种情况的数量小于剩余可填数量 对应当前所有情况所在行填上1 
			else{//这种情况的数量大于剩余可填数量 从所有情况数中选出rx个填上1 方案数为一个组合数 
				sum1[x]+=rx*h1[i]+(s1[i]-rx)*(n-h1[i])+sr1[i+1];//等于a的1的个数+当前情况下填0行的0的个数+当前情况以下的0的个数（毕竟以后就只能填0了） 
				v1[x]=C[s1[i]][rx];
				break;
			}
		}
	}
	for(int y=0;y<=n;y++){//枚举y 
		int ry=y;v2[y]=1;
		for(int i=1;i<=top2;i++){
			if(ry>=s2[i]) sum2[y]+=s2[i]*h2[i],ry-=s2[i];
			else{
				sum2[y]+=ry*h2[i]+(s2[i]-ry)*(n-h2[i])+sr2[i+1];
				v2[y]=C[s2[i]][ry];
				break;
			}
		}
	}//同上述x 
	for(int x=0;x<=n;x++) 
		for(int y=0;y<=n;y++)
			if(sum1[x]+sum2[y]-x*y-(n-x)*(n-y)==n*n)//符合情况 
				ans=(ans+v1[x]*v2[y]%mod)%mod;//a的方案数 ×b的方案数 
	printf("%lld",ans);//输出答案 
	return 0;
}//代码其实还是有点难理解的 语文表达能力有限 建议自己结合样例分析一下咯 
/*
4
0101
1011
1111
1010
*/