KD(坑爹)-tree
前言:
这玩意太抽象了,看半天才勉强算是看懂了吧,累死我了www
借鉴自大佬博客
简介
\(KDtree\)的实质类似于二叉搜索树。众所周知,二叉搜索树有如下三个性质:
- 一个节点如果它有左节点,那它的左节点的权值一定小于该节点的权值。
- 一个节点如果它有右节点,那它的右节点的权值一定大于该节点的权值。
- 它的左右子树都符合二叉搜索的性质。
而此时不同的地方,就是我们所操作的对象不同。此时我们操作的对象为一个多维数集,我们考虑如何能将这个集合拆分开。应该与二叉搜索树相似要与根节点比较大小,但是由于它有多维信息,我们要从不同的维度进行划分,即用多个超空间平面把空间分隔开,它一边的值全部小于它,另一边的值全部大于它。也就是说,我们每选择一个维度,就将空间分为两个部分。然后我们不断重复上述操作知道空间不可再分。但此时,我们又面临着两个问题。
- \(Q:\)选择哪个维度进行划分?
\(A:\)我们可以求出每个维度对应值的方差,方差大的那个说明点分布得越松散,越能取得平衡。 - \(Q:\)如何保证树尽可能的平衡?
\(A:\)我们选择分割点时尽可能的选择中位数,这样分布在两边的数就几乎相等了。
构建
选择方差最大的维度,并选择中位数作为分割点,对空间不断地进行划分,直到空间不可再分。
这里我们拿二维的来举例(别的维数咱也没法举啊)请看\(VCR\)。额不是,是下图。
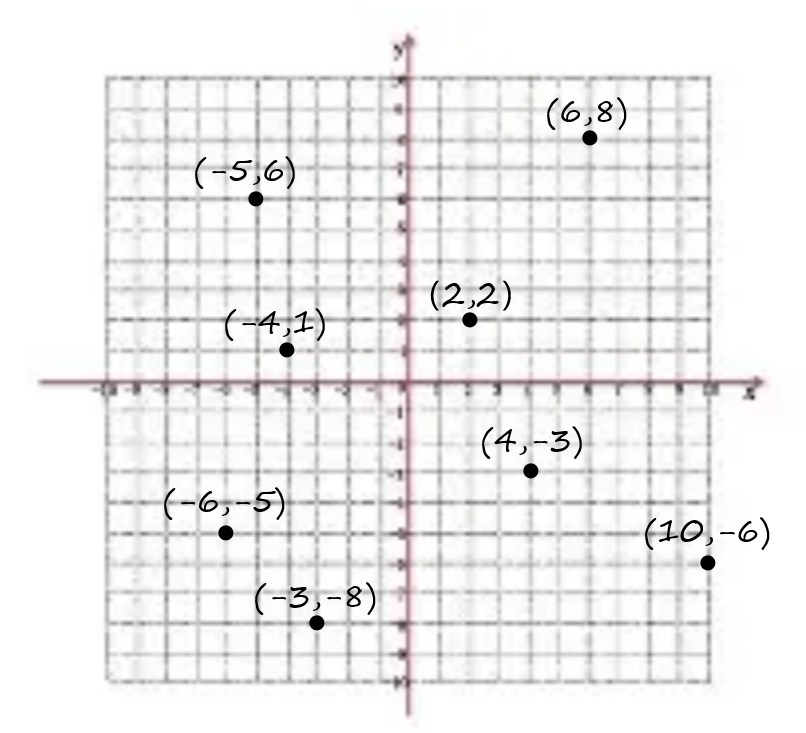
由不完全严谨的计算可得,\(x\)维的方差为30,\(y\)维的方差为29.4844,所以我们先从\(x\)维开始分割。即如下图所示
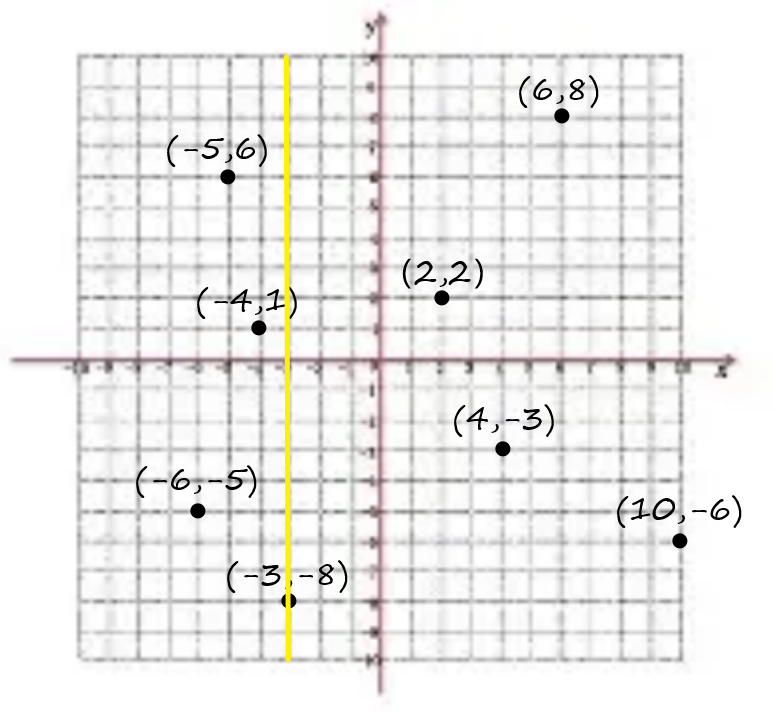
然后换\(y\)维继续分割
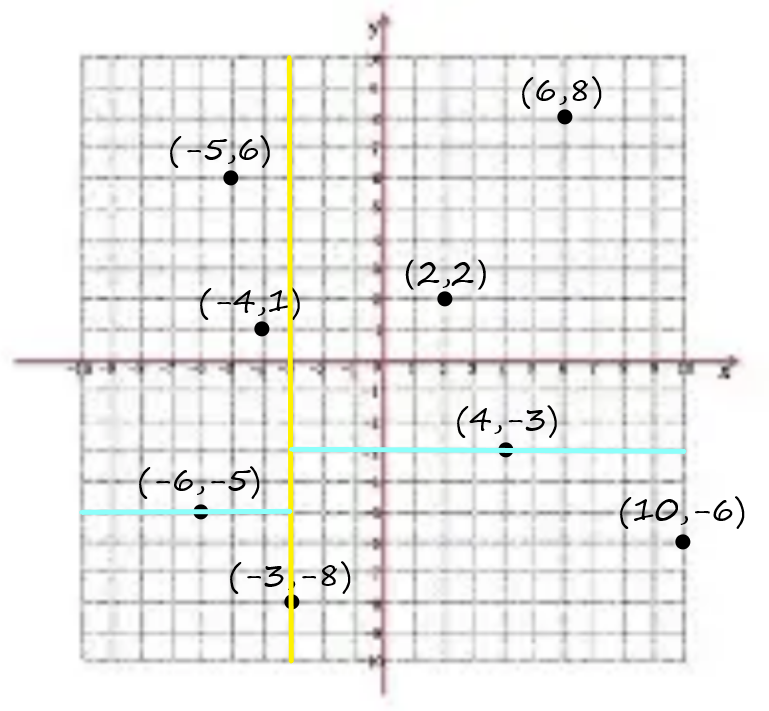
然后重复上述操作,直到空间不可再分
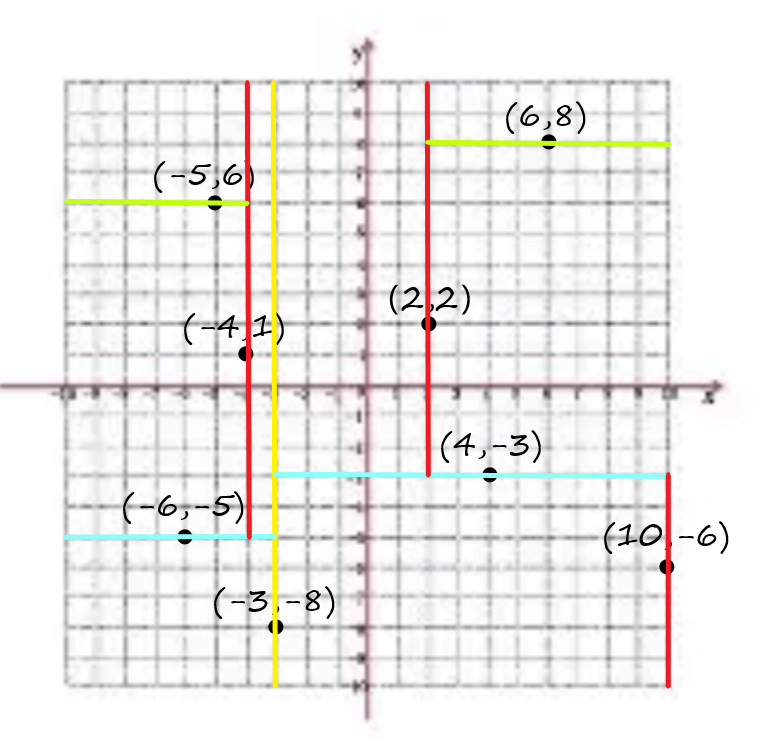
所以我们可以画出\(KD~tree\)如下图

最近查找
- 从根节点开始向下递归并比较该维度下查询值与节点值的大小直到叶子结点。若查询点小于该节点中值,则递归左子树,否则递归右子树。到叶子结点时,计算查询点到该叶子节点的距离记为当前最近邻点\(nearest\)和最小距离\(dis\)。
- 进行回溯操作,目的是找到与查询点更近的点。即判断未访问过的节点里是否有距离更小的点。如果查询点与一个父结点下的未被访问过的分支之间的距离大于\(dis\),则说明该分支内不存在与查询更近的点。回溯的判断过程是从下往上进行的,直到回溯到根结点时已经不存在与P更近的分支为止。从几何意义上来解释就是以查询点为球心,寻找是否有点在半径为\(dis\)的超球体的内部。若存在,则该点距离查询点更近。
举个栗子🌰:
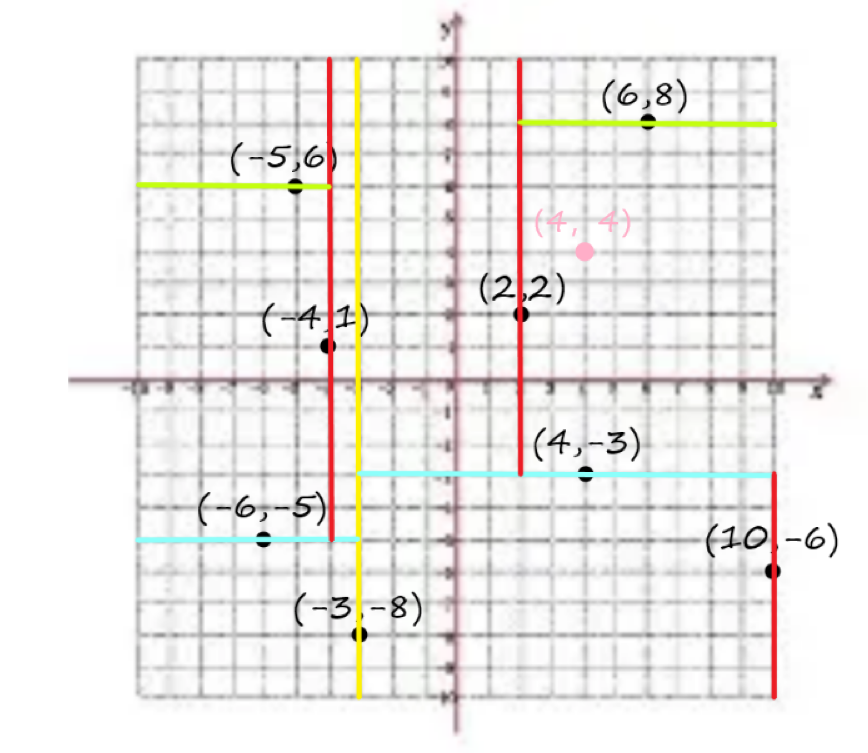
此时的查找路径为\(【(-3,-8),(4,-3),(2,2),(6,8)】\)。显然,我们能快速找到与查询点相近的叶子结点为\((6,8)\),此时\(dis\)赋值为\(4.47\),然后画圆。
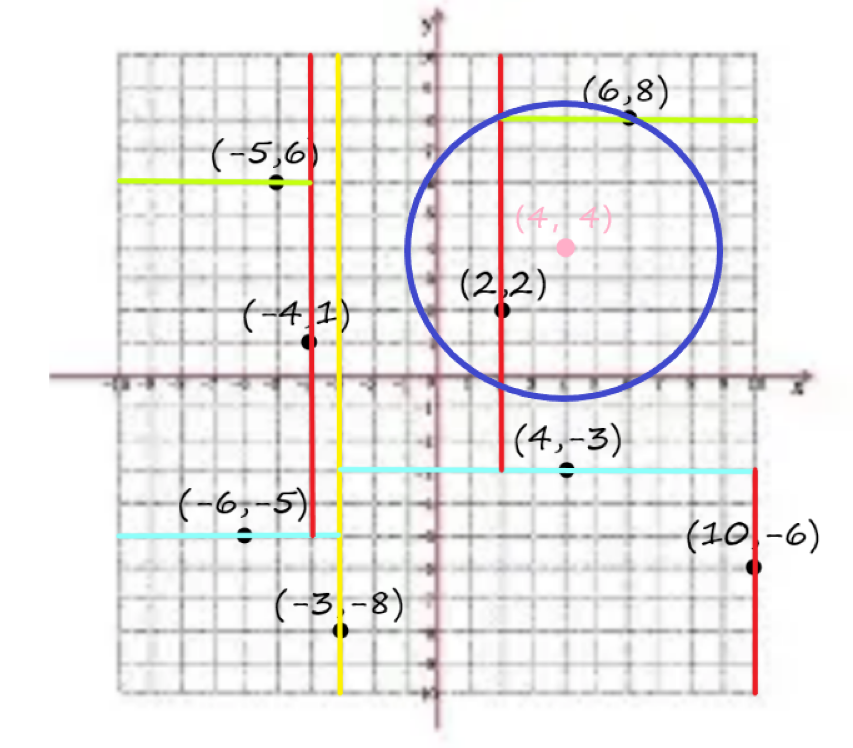
接下来我们回溯到\((2,2)\),此时我们发现\((2,2)\)与查询点的距离为\(2.83\),距离更小,因此更新\(dis\)的值。然后回溯到\((4,-3)\),我们计算出此时的距离为\(7\)大于\(dis\),所以不更新。继续回溯到\((-3,-8)\),此时的距离为\(13.89\),大于\(dis\),不更新。至此,搜索完毕,最近距离为\(4.47\)。
例题时间:P2056 [ZJOI2007] 捉迷藏
思路:
显然,这道题让我们求其他点到某一个点的最大距离和最小距离之差最小(此处的距离指曼哈顿距离)(好像有点绕口?不管了,反正大概就这个意思。)所以,我们需要遍历所有的点,并求出距离这个点最大和最小的点,这里就要用到\(KD-tree\)求距离极值了。
代码:
#include<iostream>
#include<algorithm>
#define lc tr[x].l
#define rc tr[x].r
using namespace std;
const int N=1e5+10;
int n,K,cur,root;
int ans_min=2e9,ans_max,ans=2e9;
struct node{
int l,r;
int v[2],minn[2],maxn[2];//两个维度 两个维度的最小值 最大值
bool operator <(const node &b)const{
return v[K]<b.v[K];
}
}tr[N];
inline void pushup(int x){
for(int i=0;i<=1;i++){
tr[x].maxn[i]=tr[x].minn[i]=tr[x].v[i];
if(lc) tr[x].maxn[i]=max(tr[x].maxn[i],tr[lc].maxn[i]),tr[x].minn[i]=min(tr[x].minn[i],tr[lc].minn[i]);
if(rc) tr[x].maxn[i]=max(tr[x].maxn[i],tr[rc].maxn[i]),tr[x].minn[i]=min(tr[x].minn[i],tr[rc].minn[i]);
}
}//更新维护的信息
inline int build(int l,int r,int k){
if(l>r) return 0;
K=k;//标记是是哪个维度
int mid=(l+r)>>1;
nth_element(tr+l,tr+mid,tr+r+1);//具体说明见代码下面
tr[mid].l=build(l,mid-1,k^1);
tr[mid].r=build(mid+1,r,k^1);//递推建树
pushup(mid);
return mid;
}//建树
inline int dis(int x){return abs(tr[cur].v[0]-tr[x].v[0])+abs(tr[cur].v[1]-tr[x].v[1]);}//求曼哈顿距离
inline int dis_min(int x){return (!x)?2e9:max(tr[cur].v[0]-tr[x].maxn[0],0)+max(tr[x].minn[0]-tr[cur].v[0],0)+max(tr[cur].v[1]-tr[x].maxn[1],0)+max(tr[x].minn[1]-tr[cur].v[1],0);}//最大距离
inline int dis_max(int x){return (!x)?0:max(tr[cur].v[0]-tr[x].minn[0],tr[x].maxn[0]-tr[cur].v[0])+max(tr[cur].v[1]-tr[x].minn[1],tr[x].maxn[1]-tr[cur].v[1]);}//最小距离
inline void query_min(int x){
if(!x) return ;
if(x!=cur) ans_min=min(ans_min,dis(x));//不算自身的节点
int dl=dis_min(lc),dr=dis_min(rc);
if(dl<ans_min) query_min(lc);
if(dr<ans_min) query_min(rc);//向左右子树递推求值
}//查询最小距离
inline void query_max(int x){
if(!x) return ;
if(x!=cur) ans_max=max(ans_max,dis(x));//不算自身的节点
int dl=dis_max(lc),dr=dis_max(rc);
if(dr>ans_max) query_max(rc);
if(dl>ans_max) query_max(lc);//向左右子树递推求值
}//查询最大距离
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cur++;
cin>>tr[cur].v[0]>>tr[cur].v[1];//输入
}root=build(1,n,0);//建树
for(cur=1;cur<=n;cur++){//遍历节点
ans_min=2e9;ans_max=0;
query_min(root);query_max(root);
ans=min(ans,ans_max-ans_min);
}cout<<ans;
return 0;
}
\(tips:\)nth_element表示在\(tr\)数组内找到第\(mid\)大的值,并保证在它左面的值都小于它,右面的值都大于它。但是不保证序列是有序的,时间复杂度为\(O(n)\)。


