CF1905E One-X

前言：

首次讲题，（非常） 略微紧张，讲得迷了吧噔的，差点把自己讲不会了，也不知道讲明白没有，还漏了好多注意点，而且在白板上写的字好丑【呜呜呜(╥﹏╥)】。不过可能没啥人听，所以没有人质疑我。不过，补坑是一个好习惯，所以现在补上啦~~

题目链接：CF1905E One-X

思路：

正难则反，既然考虑每个叶子结点的lca不好做，那我们不妨反过来求每一个点作为lca对答案的贡献。

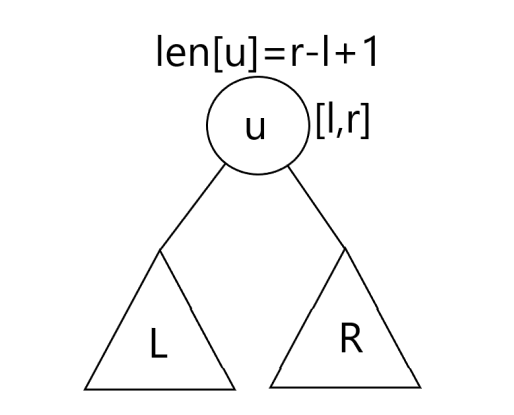
我们设当前点的编号为\(u\)，对应的区间为\([l,r]\)，所以区间长度为\(len=r-l+1\)，中点为\(mid=(l+r)>>1\).由题易得节点\(u\)对答案的贡献为从左子树选一个节点的可能性乘以从右子树选一个节点的可能性乘以该节点编号，即为\(u*(2^{mid-l}-1)*(2^{r-mid}-1)\)，上式可以化为\(u*(2^{\frac{len+1}{2}}-1)*(2^{\frac{len}{2}}-1)\).由此，我们不难发现这个式子仅与编号\(u\)和区间长度\(len\)有关。因此，我们不妨把所有长度相同的点放到一起统一计算，然后统计编号和。设左子树\(L=(len+1)>>1\)，右子树\(R=len>>1\)，\(f[x]\)表示长度为\(x\)的编号和，\(g[x]\)表示长度为\(x\)的数量。然后显然可得递推方程式为\(f[L]+=f[x]*2\)，\(f[R]+=f[x]*2+g[x]\)，\(g[L]+=g[x]\)，\(g[R]+=g[x]\)。然后记得初始化\(f[n]=g[n]=1\).防止重复遍历我们还需要一个\(map\)数组来打标记。随后在看一眼\(n\)的数据范围，\(2≤n≤10^{18}\)，有点大，所以记得开\(long \ \ long\)喔~~

代码~~

#include<iostream>
#include<map>
#include<queue>
#define int long long
using namespace std;
const int mod=998244353;
int T,n,ans;map<int,int> g,f;map<int,bool> vis;queue<int> q;
inline int qpow(int x,int y){ 
	int res=1;
	while(y){
		if(y&1) res=(res*x)%mod;
		x=(x*x)%mod;
		y>>=1;
	}
	return res;
}//快速幂 
inline void bfs(){
	f[n]=g[n]=vis[n]=1;q.push(n);//初始化 
	while(!q.empty()){
		int x=q.front();q.pop();
		if(x==1) ans=(ans+f[x])%mod;//特判特殊情况 
		else{
			int L=(x+1)>>1,R=x>>1;//左/右子树 
			ans=(ans+f[x]*(qpow(2,L)-1)%mod*(qpow(2,R)-1)%mod)%mod;
			f[L]=(f[L]+f[x]*2%mod)%mod;
			g[L]=(g[L]+g[x])%mod;
			f[R]=(f[R]+g[x]+f[x]*2%mod)%mod;
			g[R]=(g[R]+g[x])%mod;//公式见思路 
			if(!vis[L]) q.push(L),vis[L]=1;
			if(!vis[R]) q.push(R),vis[R]=1;//标记 防止搜重 
		}
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>T;
	while(T--){
		cin>>n;
		ans=0;g.clear();f.clear();vis.clear();//多组数据清空 
		bfs();
		cout<<ans<<'\n';//完结撒花~~ 
	}
	return 0;
}

后言：

没啥后言，那就放歌词吧~~ （其实就是为了放歌词的【逃】）

山河无恙 烟火寻常 可是你如愿的眺望

孩子们啊 安睡梦乡 像你深爱的那样

by：《如愿》