HZ CSP-S模拟13

前言：

不难的题目以及稀碎的成绩，貌似是普转提失败了。
附上一首来自学妹的诗

点击查看代码

收拾收拾
拾掇拾掇
整理整理
遗容遗表
滚回，
普及组罢。
普转提比赛，
直接爆炸，
滚回普及组。

不闹了不闹了，开始写正经题解啦~~

\(T1\) : \(Soso\) 的并查集写挂了（\(sosodsu\)）

题面（照样粘）：

思路：

题目都说了用并查集那就听话地用并查集喽（话说最近并查集出现的频率有点高诶）。最简单的就是用普通并查集模拟题目的过程，然后直接记录答案就好了。\(But...\)很显然它会超时。具体的时间复杂度是多少捏？如果我没有算错的话，大概可能应该或许\(maybe\)是\(O(n^2)\)的。然后，考虑优化，这里使用了带权并查集（其实不用专门去学，跟普通并查集差不多）。现在复杂就大概降为了\(O(nlogn)\)左右。具体实现细节见代码注释叭~~

点击查看代码

//带权并查集 
#include<iostream>
#define int long long
using namespace std;
const int N=5e5+5,mod=998244353;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}
inline void write(int x){if(x<0)x*=-1,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');return;}
int m,n,x,y,ans,fa[N],a[N],flag[N],val[N];
inline int find(int x){
	if(x==fa[x]) return x;//到根节点了 
	int father=fa[x];//先把它的父亲记录下来 
	fa[x]=find(fa[x]);//路径压缩 
	val[x]=(val[x]+val[father]-a[father]+mod)%mod;
	//把该点到其所在树的根节点之间的值求出来 具体原理见代码后面 
	return fa[x];
}
inline void merge(int x,int y){
	fa[y]=x;//合并 
	val[y]=(val[x]+val[y])%mod;//两棵子树合并 
}
signed main(){
//	freopen("sosodsu.in","r",stdin);
//	freopen("sosodsu.out","w",stdout);
	n=read();m=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		val[i]=a[i];
		fa[i]=i;
	}//初始化 
	for(int i=1;i<=m;i++){
		x=read();y=read();
		int a=find(x),b=find(y);
		ans=(ans+(val[x]+val[y])%mod)%mod;//求值 
		if(a!=b) merge(a,b);//合并 
	}
	write(ans%mod);
	return 0;
}

补坑：

举个栗子

原来的图：

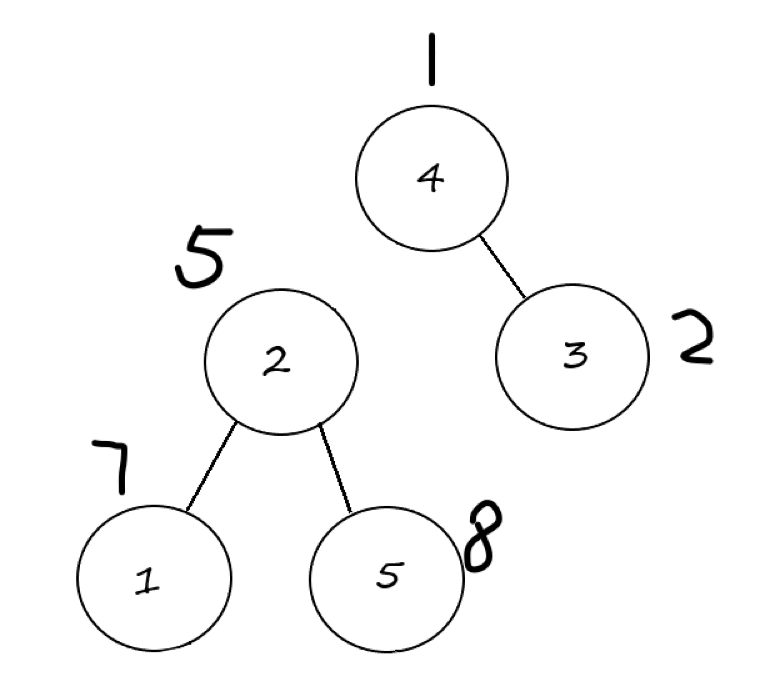
更新以后的图：

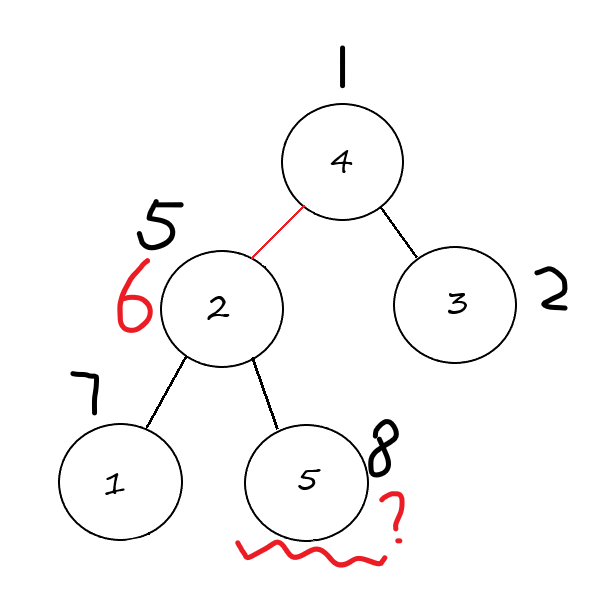
此时，\(val[2]=a[4]+a[2],val[5]=a[2]+a[5]\)，路径压缩以后变为，\(val[5]=a[4]+a[2]+a[5]=val[2]+val[5]-a[2].\)

\(T2\)：迁跃（\(clock\)）

题面：

思路：

树上最值考虑树形\(dp\)，按照树形\(dp\)的套路来说肯定有一维为当前节点，而此时我们还有另一个问题需要考虑，就是是否需要使用迁跃返回该点。于是，第二维的状态有了。所以，完整的\(dp\)状态为\(f[i][0/1]\)表示不回/回到\(i\)点。返回的\(dp\)方程也比较简单：

\(f[x][1]=max(0,f[to][1]-k)\). 要么在该点停止，要么下去又返回来，取较大值。

而不返回的方程式在返回的方程式基础上进行烧烤（思考）

再返回的基础上，用下一个遍历到的点减去从该点过去变化的权值，再加上两点之间连边的权值（相当于回溯又重新递推）。

代码：

点击查看代码

//树形dp 
#include<iostream>
#define int long long
using namespace std;
const int N=1e5+5;
int n,k,u,v,c,ans,f[N][2],cnt,head[N],dep[N];
struct node{int to,val,nxt;}e[N<<1];
inline void add(int x,int y,int z){
	e[++cnt].to=y;
	e[cnt].val=z;
	e[cnt].nxt=head[x];
	head[x]=cnt;
}//建边 
inline void dfs(int x,int fa){
	int tmp=0;
	dep[x]=dep[fa]+1;//深度 
	for(int i=head[x];i;i=e[i].nxt){
		int y=e[i].to;
		if(y==fa) continue;//不能吃回头草 
		dfs(y,x);//继续遍历 
		f[x][1]+=max(0ll,f[y][1]-k+e[i].val);//返回的方程式 
		tmp=max(tmp,max(f[y][0],f[y][1])-max(0ll,f[y][1]-k+e[i].val)+e[i].val);//不返回的 
	}
	f[x][0]=f[x][1]+tmp;
}
signed main(){
	freopen("clock.in","r",stdin);
	freopen("clock.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(int i=1;i<n;i++){
		cin>>u>>v>>c;
		add(u,v,c);add(v,u,c);
	}dfs(1,0);
	cout<<f[1][0]<<'\n';//输出答案 
	return 0;
}