两道动态规划的作业题
Question1
用动态规划方法手工求解下面的问题：
某工厂调查了解市场情况，估计在今后四个月内，市场对其产品的需求量如下表所示。
|
时期（月） |
需要量（产品单位） |
|
1 2 3 4 |
2 3 2 4 |
已知：对每个月来讲，生产一批产品的固定成本费为 3 (千元)，若不生产，则为零。每生产单位产品的成本费为 1 （千元)。同时，在任何一个月内，生产能力所允许的最大生产批量为不超过6个单位。又知每单位产品的库存费用为每月 0.5 （千元），同时要求在第一个月开始之初， 及在第四个月末，均无产品库存。 问：在满足上述条件下，该厂应如何安排各个时期的生产与库存，使所花的总成本费用最低？
要求：写出各种变量、状态转移方程、递推关系式、和详细计算步骤。
Solution：
阶段：按月份时间进行阶段划分，i表示第i月
状态：月初时的库存量S
决策集合：第i月生产单位产品的数量ki，且0<=ki<=6
不妨设第i月的产品需求量为ai，则状态间的转移关系为Si+1 = Si + ki – ai。我们设F[i , s]为从第i月到第n（n=4）月的最低总成本费用，则不难得出如下状态转移方程的递推关系式：
其中：w=0 (k==0) 或 w=3 + 1*k (1<=k<=6)
边界条件：F[5,0] = 0；s + k –a[i] >=0；
目标结果状态：F[1,0]即所求最低成本费用
手工求解计算详细计算步骤如下：
|
i=4 |
|||||||||
|
状态 |
k=0 |
k=1 |
k=2 |
k=3 |
k=4 |
k=5 |
k=6 |
Min |
决策 |
F[4,0] |
N/A |
N/A |
N/A |
N/A |
7 |
8 |
9 |
7 |
4 |
F[4,1] |
N/A |
N/A |
N/A |
6.5 |
7.5 |
8.5 |
9.5 |
6.5 |
3 |
F[4,2] |
N/A |
N/A |
6 |
7 |
8 |
9 |
10 |
6 |
2 |
F[4,3] |
N/A |
5.5 |
6.5 |
7.5 |
8.5 |
9.5 |
10.5 |
5.5 |
1 |
F[4,4] |
2 |
6 |
7 |
8 |
9 |
10 |
11 |
2 |
0 |
|
i=3 |
|||||||||
|
状态 |
k=0 |
k=1 |
k=2 |
k=3 |
k=4 |
k=5 |
k=6 |
Min |
决策 |
|
F[3 , 0] |
N/A |
N/A |
12 |
12.5 |
13 |
13.5 |
11 |
11 |
6 |
|
F[3 , 1] |
N/A |
11.5 |
12 |
12.5 |
13 |
10.5 |
N/A |
10.5 |
5 |
|
F[3 , 2] |
8 |
11.5 |
12 |
12.5 |
10 |
N/A |
N/A |
8 |
0 |
|
F[3 , 3] |
8 |
11.5 |
12 |
9.5 |
N/A |
N/A |
N/A |
8 |
0 |
|
F[3 , 4] |
8 |
11.5 |
9 |
N/A |
N/A |
N/A |
N/A |
8 |
0 |
|
F[3 , 5] |
8 |
8.5 |
N/A |
N/A |
N/A |
N/A |
N/A |
8 |
0 |
|
F[3 , 6] |
5 |
N/A |
N/A |
N/A |
N/A |
N/A |
N/A |
5 |
0 |
|
i=2 |
|||||||||
|
状态 |
k=0 |
k=1 |
k=2 |
k=3 |
k=4 |
k=5 |
k=6 |
Min |
决策 |
|
F[2 , 0] |
N/A |
N/A |
N/A |
17 |
17.5 |
16 |
17 |
16 |
5 |
|
F[2 , 1] |
N/A |
N/A |
16.5 |
17 |
15.5 |
16.5 |
17.5 |
15.5 |
4 |
|
F[2 , 2] |
N/A |
16 |
16.5 |
15 |
16 |
17 |
18 |
15 |
3 |
|
F[2 , 3] |
12.5 |
16 |
14.5 |
15.5 |
16.5 |
17.5 |
15.5 |
12.5 |
0 |
|
F[2 , 4] |
12.5 |
14 |
15 |
16 |
17 |
15 |
N/A |
12.5 |
0 |
|
F[2 , 5] |
10.5 |
14.5 |
15.5 |
16.5 |
14.5 |
N/A |
N/A |
10.5 |
0 |
|
F[2 , 6] |
11 |
15 |
16 |
14 |
N/A |
N/A |
N/A |
11 |
0 |
|
i=1 |
|||||||||
|
状态 |
k=0 |
k=1 |
k=2 |
k=3 |
k=4 |
k=5 |
k=6 |
Min |
决策 |
F[1,0] |
N/A |
N/A |
21 |
21.5 |
22 |
20.5 |
21.5 |
20.5 |
5 |
由上表不难得出，所花的总成本费用最低为20.5（千元），该情况下的由递推公式逆推可得决策安排如下：第一个月生产5个单位产品，第二个月生产0个，第三个月生产0个，第四个月生产6个，该方案可使总成本最低，即20.5（千元）。
源代码：
#include<iostream> using namespace std; double f[5][7] = {0}; int a[5] = {0,2,3,2,4}; int main() { for(int i=0;i<5;i++) for(int j=0;j<=7;j++) f[i][j] = 1000; f[5][0] = 0; for (int i=4;i>=1;i--){ for(int s=0;s<=6;s++) { int temp = 0; for(int k=i;k<=4;k++) temp+= a[k]; if (s>temp) continue; double min = 10000; int u = -1; for(int j=0;j<=6;j++){ int w = 3 + j; if (j==0) w = 0; if (s + j - a[i] >= 0 && s + j - a[i] <=6) { if (min>f[i+1][s+j-a[i]] + w + 0.5*s) { min = f[i+1][s+j-a[i]] + w + 0.5*s; u = j; } } } f[i][s] = min; } } cout<<"Answer:"<<f[1][0]<<endl; return 0; }
Question2：
用动态规划方法编程求解下面的问题：
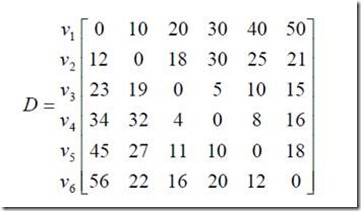
某推销员要从城市 v1出发，访问其它城市 v2，v3，…，v6各一次且仅一次，最后返回 v1。D 为各城市间的距离矩阵。
问：该推销员应如何选择路线，才能使总的行程最短？
要求：写出递推关系式、伪代码和程序相关说明，并分析时间复杂性。（请遵守第一节课提出的有关 assignment 的要求）
Solution：
设F[i,s]表示当前所在节点为i，已经走过的节点集合为s的最短路程。决策为选择下一个节点k，因此，的状态转移方程的递推关系式：
其中，d[i,k]表示i节点到k节点的距离
源代码：
一些说明：有几个关键问题需要说明
1、集合如何表示，表示集合有个很好的方法，就是使用二进制模型。例如：11101表示含有1、3、4、5元素的集合。这一一个十进制的数字就可以代表一个集合。
2、那么如何进行对集合的操作呢？对于位运算，我们可以利用1的左右移（<< or >>）来判断是否包含某个元素。S-{k}也就是方便的表示为：S[j] & (length-(1<<(k-1)))，其中length=(1 << (n-1)) - 1;
3、
该图表示一个求解模型树，不难发现含有一个元素的集合要先进行计算，才可以计算还有两个元素状态的解空间，这样就要求不同集合之间是有序的，即含有二进制1的个数少的要排在前面。这样就不会在计算过程中，出现使用未计算结果的情况。实现方法可以使用预排序。因为排序的复杂度相对于整体算法的复杂性而言，是很小的，不会过多影响性能。
时间复杂度：
由于集合的状态个数为2n-1 个，还需要枚举每个结点，以及每个集合中的元素，因此整个算法的近似复杂度为O(n2*2n)。
最后给出源代码（水平有限仅供参考）：
#include<iostream> #include<stdio.h> #include<algorithm> using namespace std; const int maxnum = 100001; int Count(int v){ int num = 0; while(v){ v &= (v-1); num ++; } return num; } bool cmp(int a , int b){ int count1_a = Count(a); int count1_b = Count(b); return count1_a < count1_b; } bool existkey( int key , int S) { int p = 1; p = p << (key-1); p = p & S; if (p>0) return true; else return false; } void getElements( int S , int * arr , int length , int &return_len) { int p = 1; int pos = 0; for(int i=0;i<length;i++){ if (p == (p&S)){ arr[pos++] = i+1; } p = p << 1; } return_len = pos; } int main() { freopen("input.txt","r",stdin); int n = 0 ; cin >> n; int F[10][100]; int S[1000]; int elements [10]; int distance[10][10]; int length_elements = 0; for(int i=0 ; i<n ; i++ ){ for (int j=0 ; j<n ; j++) { cin>>distance[i][j]; } } for (int i=1 ; i<=n ;i++) F[i][0] = distance[i][0]; int length = (1 << (n-1)) - 1; for (int i=1 ; i<=length ; i++){ S[i] = i; } sort(S,S+length,cmp); S[0] = 0; for (int j=1 ; j<=length ; j++) { for(int i=1 ; i<n ; i++) { if (existkey(i , S[j]) != true){ getElements(S[j] , elements, n , length_elements); int min = maxnum; for (int p=0 ; p<length_elements ; p++){ int k = elements[p]; int jj = S[j] & (length-(1<<(k-1))) ; if (min > ( F[k][jj] + distance[i][k] ) && k!=i ) min = F[k][jj] + distance[i][k]; } F[i][S[j]] = min; } } } int ans = maxnum; for (int i=1 ; i<n ; i++){ int j = length & (length -(1<<(i-1))); if (ans > F[i][j] + distance[0][i]) ans = F[i][j] + distance[0][i]; } cout<<"Answer:\t"<<ans<<endl; return 0; }
