树状数组（单点查询，单点修改，区间查询，区间修改）

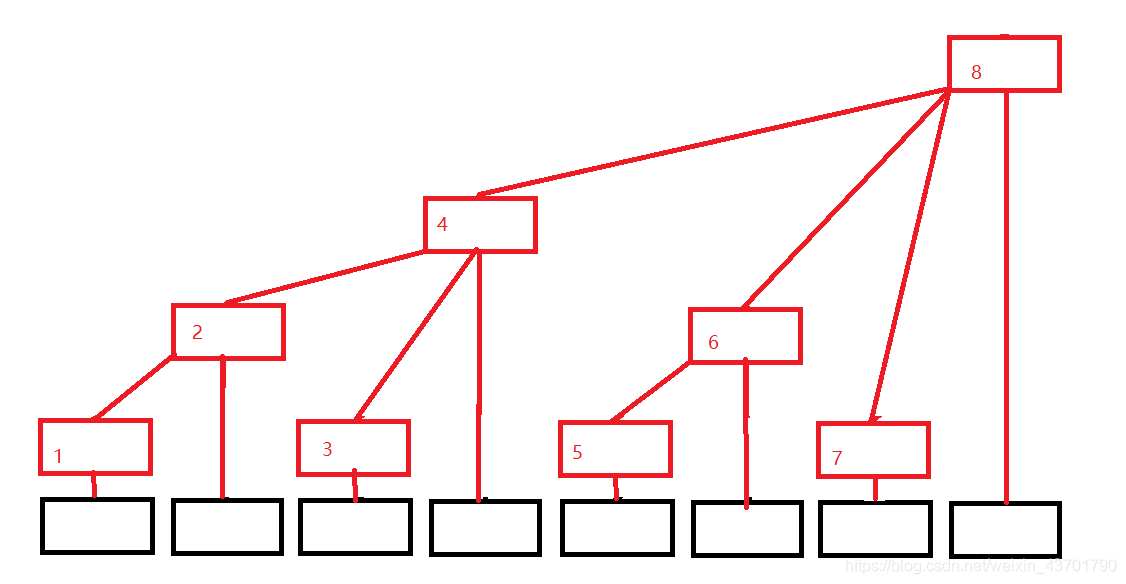
树状数组就是形如上图的一种数据结构

单点查询

lowbit运算设计的很巧妙

int lowbit(int x){
	return x & -x;
}

可以求出一个数的二进制表示中最低位的1和后面的0组成的数字

例如：lowbit(7)，7的二进制是111，lowbit(7)就是，最低为的1和后面的0（没有0）组成的数，二进制表示为1，即数字1

用树状数组维护的实质上是一个前缀和，每一个偶数位置的值对应的是一个前缀和，如果是2的整数次幂则维护的是从1到当前位置的前缀和，在查询的时候，例如

查询 5 位置处的前缀和，将 5 写成二进制表示（101），首先加上 a[]的值，即a[5]的值，然后把最低为的1变为0即

x -= lowbit(x);

然后二进制表示变成了100，再加上a[4]的值，然后再次进行上述运算，直到 x 为 0 退出，由此我们得到了 a[5] = a[4] + a[5]

而a[4]正好是 4 的前缀和，再加上 5 处的值即为正确答案，既然知道了树状数组是维护的前缀和，两个前缀和做差即是单点的值

如果查询 7 位置的前缀和的值，由上图可知道sum =  a[7] + a[6] + a[4]其中a[7]对应7处的值，a[6]是5和6的前缀和，a[4]是1到4的前缀和

int get(int x){
	int res = 0;
	while (x){
		res += a[x];
		x -= lowbit(x);
	}
	return res;
}

单点修改

道理和查询一样，如果要将 5 处的函数值加上 d ，我们不仅要修改 5 处的函数值，还要修改包含 5 的前缀和的函数值，而通过每次让 x = x + lowbit(x)恰好可以得到每一个包含 x 的前缀和的位置，因此可以从x开始，每次让a[x] += d，当 x 大于最大范围 n 时，结束

void add(int x, int d){
	while (x <= n){
		a[x] += d;
		x += lowbit(x);
	}
}

区间修改

树状数组本身时不支持区间查询的，但是如果我们做一些手脚，把本来维护的前缀和的数组a，变成 a 的差分数组，那么每次查询到的前缀和就是原本的值，而在修改的时候，因为差分区间内增加相同的值，中间的差值不变，只有两端的值改变，因此可以用两次单点修改来完成区间修改

void add1(int x, int d){//b为差分数组 通过差分区间实现区间修改 
	while (x <= n){
		b[x] += d;
		x += lowbit(x);
	}
}

（区间查询和区间修改同时进行，日后补上QwQ）