Experiment3

Task1

#include <stdio.h>
char score_to_grade(int score); // 函数声明
int main() {
	int score;
	char grade;
	while(scanf("%d", &score) != EOF) {
		grade = score_to_grade(score); // 函数调用
		printf("分数: %d, 等级: %c\n\n", score, grade);
	}
	return 0;
}
// 函数定义
char score_to_grade(int score) {
	char ans;
	switch(score/10) {
		case 10:
		case 9:
			ans = 'A';
			break;
		case 8:
			ans = 'B';
			break;
		case 7:
			ans = 'C';
			break;
		case 6:
			ans = 'D';
			break;
		default:
			ans = 'E';
	}
	return ans;
}

问题1 函数 score_to_grade 的功能是什么？形参类型、返回值类型分别是什么？

为分数定级；形参score类型为整型，返回值为char字符型

问题2 如果line21-28改成以下写法，代码存在哪些问题？请逐一指出。

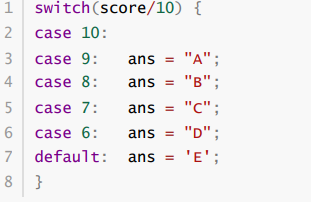
未设置break，一个条件符合后会连带执行下面所有语句。

Task 2

#include <stdio.h>
int sum_digits(int n); // 函数声明
int main() {
	int n;
	int ans;
	while(printf("Enter n: "), scanf("%d", &n) != EOF) {
		ans = sum_digits(n); // 函数调用
		printf("n = %d, ans = %d\n\n", n, ans);
	}
	return 0;
}
// 函数定义
int sum_digits(int n) {
	int ans = 0;
	while(n != 0) {
		ans += n % 10;
		n /= 10;
	}
	return ans;
}

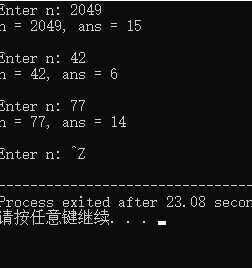
问题1：函数 sum_digits 的功能是什么？

计算各数位数值和

问题2：如果把函数 sum_digits 定义成如下实现方式，能实现同样的输出吗？如果能，说明两种实现方式的算法思维区别；如果不能，分析原因。

能实现，不过是用递归定方式实现的。

Task 3

#include <stdio.h>
int power(int x, int n); // 函数声明
int main() {
	int x, n;
	int ans;
	while(printf("Enter x and n: "), scanf("%d%d", &x, &n) != EOF) {
		ans = power(x, n); // 函数调用
		printf("n = %d, ans = %d\n\n", n, ans);
	}
	return 0;
}
// 函数定义
int power(int x, int n) {
	int t;
	if(n == 0)
		return 1;
	else if(n % 2)
		return x * power(x, n-1);
	else {
		t = power(x, n/2);
		return t*t;
	}
}

问题1: 函数 power 的功能是什么？

实现指数运算（算x的n次幂）

问题2：函数 power 是递归函数吗？如果是，找出递归模式。写出这个递归模式对应的数学公式模型

是。

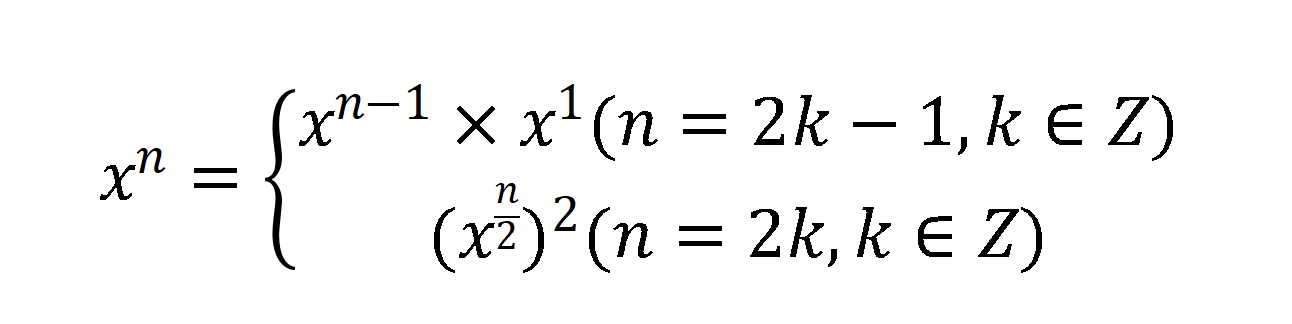
Task 4

#include <stdio.h>
#include <math.h>
int is_prime(int x);// 函数声明
int main() {
	int x,i,cnt=0;
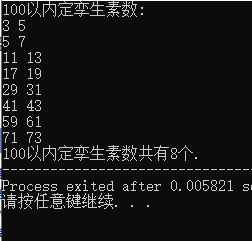
	printf("100以内定孪生素数:\n");
	for (i=1;i<=98;i++){
		if (is_prime(i) && is_prime(i+2)) {
			printf("%d %d\n",i,i+2);
			cnt++;	
		}
	}
	printf("100以内定孪生素数共有%d个.",cnt);
	return 0;
}
int is_prime(int x){
	int sq = sqrt(x),i;
	if (x<2) return 0;
	for (i=2;i<=sq;i++){
		if (x%i == 0) return 0;
	}
	return 1;
}

Task 5

递归

int func(int n,int m){
	if (n<m) return 0;
	else if (n == m || m == 0) return 1;
	else return func(n-1,m)+func(n-1,m-1); 
}

迭代

#include <stdio.h>
int main() 
{
	double n,m,tmp,ans=1;
	while(scanf("%lf%lf",&m,&n) == 2) {
		printf("n = %.0lf,m = %.0lf",m,n);
		if (m<n) {
			ans=0;
		} else {
			tmp=m-n;
			if (n>m/2) n=tmp;
			while(m!=tmp) {
				ans*=m/n;
				n--;
				m--;
			}
		}
		printf(",ans = %.0lf\n",ans);
		ans=1; 
	}
	return 0;
}

Task 6

#include <stdio.h>
#include <limits.h>
// 函数声明
int gcd(int a,int b,int c);
// 待补足....
int main() {
	int a, b, c;
	int ans;
	while(scanf("%d%d%d", &a, &b, &c) != EOF) {
		ans = gcd(a, b, c); // 函数调用
		printf("最大公约数: %d\n\n", ans);
	}
	return 0;
}
int gcd(int a,int b,int c) {
	int i=INT_MAX;
	if(a<=i) i=a;
	if(b<=i) i=b;
	if(c<=i) i=c;
	for (i; i>=1; i--) {
		if(a%i == 0 && b%i == 0 && c%i == 0) return i;
	}
	return -1;
}

Task 7

#include <stdio.h>
// 函数声明
void printcharman(int);
// 待补足....
int main() {
	int n;
	while(scanf("%d",&n) != EOF){
		printcharman(n);
	}
	
	return 0;
}


void printcharman(int n) {
	int i=2*n-1;//顶端小人数
	for(i; i>=1; i-=2) {
		int k;
		for(k=n-(i+1)/2;k>0;k--){
			printf("\t");
		} 
		for(k=i; k>=1; k--) {
			printf(" o\t");
		}
		printf("\n");
		for(k=n-(i+1)/2;k>0;k--){
			printf("\t");
		} 
		for(k=i; k>=1; k--) {
			printf("<H>\t");
		}
		printf("\n");
		for(k=n-(i+1)/2;k>0;k--){
			printf("\t");
		} 
		for(k=i; k>=1; k--) {
			printf("I I\t");
		}
		printf("\n");
	}
}