WQS二分学习笔记

WQS二分学习笔记

参考：https://www.cnblogs.com/dummyummy/p/10574081.html
完全没看懂……

事情的起因，是一道叫做林克卡特树的题。

题目大意：从一棵树中选出 \(k+1\) 条非相邻链，要求链的权值和尽量大。有负权边。

首先能想到一个简单的DP，\(f[i][j][0/1/2]\)：以\(i\)为根的子树中，选了\(j\)条链，0：\(i\)没选 1：\(i\)在链的端点上

2：\(i\)在一条链中间

时间复杂度\(O(nk^2)\)，可以摸到45分的好成绩。

优化

很明显我们还需要进一步优化。

对\(k\)打表后我们发现，\(k\)递增的情况下\(f[1][k]\)是一个上凸函数（图像类似于二次函数图像）。

简略证明:由于图中存在负权边，所以选边时肯定优先不选这些负权边。但随k的增大负权边会被删完，此时只能开始不选正权边，于是出现了答案先上升后下降的趋势

所以，我们可以使用一种叫WQS二分的方法进行优化。

WQS二分

wqs二分一般用于一种特殊的背包问题：有\(n\)个带权物品，选用物品时有一定限制，需要取\(m\)个物品，要求取出的权值和尽量大。且若设取出权值和为\(f(m)\)，\(f(m)\)必须为关于\(m\)的上凸函数。

假设\(f(m)\)图像如下

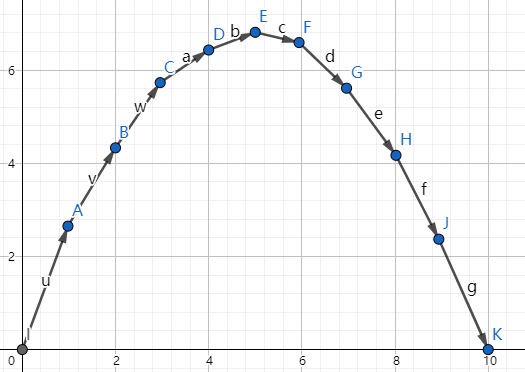
我们先画出一条这个函数的切线

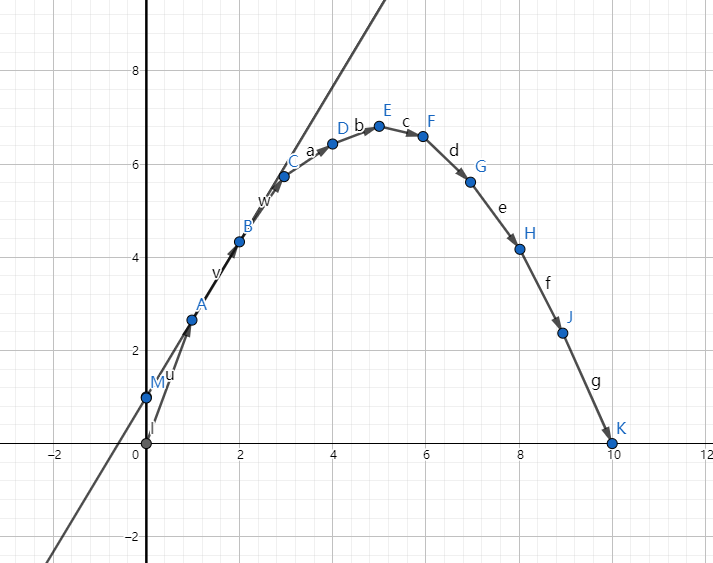
设这条切线的解析式为\(f(x)=k\times x+b\)。则切线在纵坐标轴上的截距可以用\(b=f(x)-k\times x\)表示。同时，有一个显而易见的结论：平移这条切线，保证与函数相交的情况下这条直线的纵截距不会超过切线的截距。

所以，只要我们能找到\(b_{max}\)，就能求出当前斜率下的\(f(x)_{max}\)，进而求出当前切点的\(x\)值。

我们再观察\(b\)的表达式。观察到\(f(x)\)的含义是取\(x\)个带权值的物品时最大权值和。所以，我们想到把所有物品的权值都\(-k\)，就能完美地用一个新函数\(f'(x)\)来表示出\(b\)。

为了验证当前斜率是否是答案，我们可以用\(f'(x)\)进行不限物品数量的动态规划，同时记录下\(f(x)\)的最佳转移点。取出最佳转移点的物品使用量，再与要求的量\(m\)进行比较。如何调整斜率根据题目而定。若最佳转移点有多个，我们可以选择取靠后的哪个。

于是，我们成功把林克卡特树优化到了\(nlog(k)\)。
我来送个码

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=300010;
typedef long long ll;
const ll inf=1000000000000000;
struct edge{
	int next,to;
	ll dis;
}g[maxn<<1];
int head[maxn],cnt;
void add(int from,int to,ll dis)
{
	g[++cnt].dis=dis;
	g[cnt].next=head[from];
	g[cnt].to=to;
	head[from]=cnt;
}
int n,k;
struct node{
	ll val,cnt;
}f[maxn][3];
bool operator<(node a,node b)
{
	if(a.val!=b.val)return a.val<b.val;
	else return a.cnt<b.cnt;
}
node operator+(node a,node b)
{
	return (node){a.val+b.val,a.cnt+b.cnt};
}
node New(node a,ll val,ll cnt)
{
	a.cnt+=cnt;
	a.val+=val;
	return a;
}
ll LIM;
void dp(int x,int fa)
{
	f[x][0]=(node){0,0};f[x][1]=(node){-inf,0};f[x][2]=(node){-LIM,1};
	for(int i=head[x];i;i=g[i].next)
	{
		int v=g[i].to;ll d=g[i].dis;
		if(v==fa)continue;
		dp(v,x);
		node tmp=max(f[v][0],max(f[v][1],f[v][2]));
		f[x][2]=max(f[x][2]+tmp,f[x][1]+max(New(f[v][1],d+LIM,-1),New(f[v][0],d,0)));
		f[x][1]=max(f[x][1]+tmp,f[x][0]+max(New(f[v][0],d-LIM,1),New(f[v][1],d,0)));
		f[x][0]=f[x][0]+tmp;
	}
}
bool check(ll lim)
{
	LIM=lim;
	dp(1,0);
	return max(f[1][0],max(f[1][1],f[1][2])).cnt<k;
}
int main()
{
	scanf("%d%d",&n,&k);
	int i,j;
	k+=1;
	for(i=1;i<n;i++)
	{
		int a,b;
		ll c;
		scanf("%d%d%lld",&a,&b,&c);
		add(a,b,c);
		add(b,a,c);
	}
	ll L=-inf,R=inf,ans=0;
	while(L<=R){
		ll mid=((L+R)>>1);
		if(check(mid))R=mid-1;
		else ans=mid,L=mid+1;
	}
	check(ans);
	printf("%lld\n",max(f[1][0],max(f[1][1],f[1][2])).val+ans*k);
}