1、最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

 1 public class Solution {
 2     public String longestPalindrome(String s) {
 3         int len=s.length();
 4         boolean dp[][]=new boolean[len][len];
 5         int maxlen=1;
 6         int begin=0;
 7         // 初始化：所有长度为 1 的子串都是回文串
 8         for (int i = 0; i < len; i++) {
 9             dp[i][i] = true;
10         }
11         char[] str=s.toCharArray();
12         for(int l=2;l<=len;l++){//控制子串长度
13             for(int i=0;i<len;i++){
14                 int j=i+l-1;
15                 if(j>=len)break;
16                 if(str[i]!=str[j]){
17                     dp[i][j]=false;
18                 }else{
19                     if(j-i<=2){
20                         dp[i][j] = true;
21                     }else{
22                         dp[i][j]=dp[i+1][j-1];
23                     }
24                 }
25                 if(dp[i][j]&&l>maxlen){
26                 maxlen=l;
27                 begin=i;
28                 }
29             }
30         }
31         return s.substring(begin,begin+maxlen);
32     }
33 }
View Code

2、接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

 

 1 //按行统计
 2 class Solution {
 3     public int trap(int[] height) {
 4         int sum = 0;
 5         int max = getMax(height);//找到最大的高度，以便遍历。
 6         for (int i = 1; i <= max; i++) {
 7             boolean isStart = false; //标记是否开始更新 temp
 8             int temp_sum = 0;
 9             for (int j = 0; j < height.length; j++) {
10                 if (isStart && height[j] < i) {
11                     temp_sum++;
12                 }
13                 if (height[j] >= i) {
14                     sum = sum + temp_sum;
15                     temp_sum = 0;
16                     isStart = true;
17                 }
18             }
19         }
20         return sum;
21     }
22     private int getMax(int[] height) {
23             int max = 0;
24             for (int i = 0; i < height.length; i++) {
25                 if (height[i] > max) {
26                     max = height[i];
27                 }
28             }
29             return max;
30     }
31 }
View Code

3、最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

 1 //无后效性:到第i个位置时，设之前所有元素求和为pre，如果pre > 0，就要它，并加上nums[i]； 如果pre<=0，就不要它，取nums[i]本身。 
 2 public class Solution {
 3 
 4     public int maxSubArray(int[] nums) {
 5         int n=nums.length;
 6         int[] dp = new int[n];
 7         dp[0]=nums[0];
 8         for(int i=1;i<n;i++){
 9             if(dp[i-1]>0){
10                 dp[i]=dp[i-1]+nums[i];
11             }else{
12                 dp[i]=nums[i];
13             }
14         }
15         int sum=nums[0];
16         for(int i=0;i<n;i++){
17             sum=Math.max(sum,dp[i]);
18         }
19         return sum;
20     }
21 }
View Code

4、不同路径

一个机器人位于一个 m x n 网格的左上角 。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。

问总共有多少条不同的路径？

 1 class Solution {
 2     public int uniquePaths(int m, int n) {
 3         int[][] dp = new int[m][n];
 4         for (int i = 0; i < n; i++) dp[0][i] = 1;
 5         for (int i = 0; i < m; i++) dp[i][0] = 1;
 6         for (int i = 1; i < m; i++) {
 7             for (int j = 1; j < n; j++) {
 8                 dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
 9             }
10         }
11         return dp[m - 1][n - 1];  
12     }
13 }
View Code

 5、跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

     dp[i]：从[0,i]的任意一点处出发，你最大可以跳跃到的位置。

 1 class Solution {
 2     public boolean canJump(int[] nums) {
 3         if(nums.length==1)return true;
 4         if(nums[0]==0)return false;
 5         int[] dp=new int[nums.length];
 6         dp[0]=nums[0];
 7         for(int i=1;i<nums.length-1;i++){
 8             dp[i]=Math.max(dp[i-1],i+nums[i]);
 9             if(dp[i]>=nums.length-1){
10                 return true;
11             }
12             if(i==dp[i]){
13                 return false;
14             }
15         }
16         return true;
17 
18     }
19 }
View Code

6、不同的二叉搜索树

 

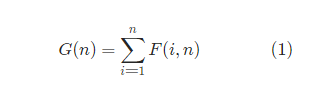
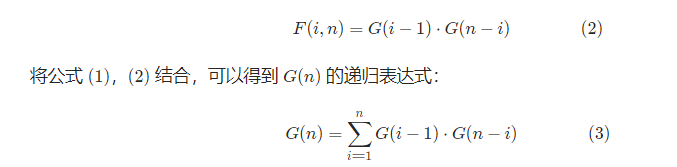
 1 class Solution {
 2     public int numTrees(int n) {
 3         int[] G = new int[n + 1];
 4         G[0] = 1;
 5         G[1] = 1;
 6 
 7         for (int i = 2; i <= n; ++i) {
 8             for (int j = 1; j <= i; ++j) {
 9                 G[i] += G[j - 1] * G[i - j];
10             }
11         }
12         return G[n];
13     }
14 }
View Code

7、杨辉三角

 1 class Solution {
 2     public List<List<Integer>> generate(int numRows) {
 3         ArrayList<List<Integer>>  list=new ArrayList<>();
 4         int[][] dp=new int[numRows][numRows];
 5         for(int i=0;i<numRows;i++){
 6             ArrayList<Integer> row=new ArrayList<>();
 7             for(int j=0;j<=i;j++){
 8                 if(j==0 || j == i){
 9                     dp[i][j] = 1;
10                 }else{
11                     dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
12                 }
13                 row.add(dp[i][j]);
14             }
15             list.add(row);
16         }
17         return list;
18     }
19 }
View Code

8、买卖股票

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        if(len < 2) return 0;
        int[][] dp = new int [len][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1; i < len; i++){
            // 这里dp[i - 1][1] + prices[i]为什么能保证只卖了一次，因为下面一行代码买的时候已经保证了只买一次，所以这里自然就保证了只卖一次，不管是只允许交易一次还是允许交易多次，这行代码都不用变，因为只要保证只买一次（保证了只卖一次）或者买多次（保证了可以卖多次）即可。
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            //  - prices[i]这里可以理解为dp[0][0] - prices[i]，这里为什么是dp[0][0] - prices[i]，因为只有这样才能保证只买一次，所以需要用一开始初始化的未持股的现金dp[0][0]减去当天的股价
            dp[i][1] = Math.max(dp[i - 1][1], - prices[i]);
              // 如果题目允许交易多次，就说明可以从直接从昨天的未持股状态变为今天的持股状态，因为昨天未持股状态可以代表之前买过又卖过后的状态，也就是之前交易过多次后的状态。也就是下面的代码。
            //dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[len - 1][0];
    }
}